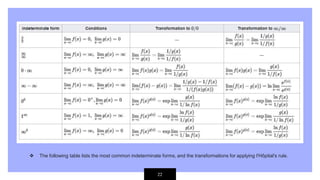
The document discusses indeterminate forms in calculus, which arise when evaluating limits that do not provide sufficient information to determine the original limit. It outlines seven types of indeterminate forms and explains l'Hôpital's rule, a method to evaluate limits of the forms 0/0 and ∞/∞. Additionally, the document provides examples of applying these concepts to solve specific limit problems.

1. INDETERMINATE
FORM
By
SHIVAM SHARMA
BWU/BTS/20/122

2. CONTENTS:-
2
▹ HISTORY
▹ DEFINITION
▹ TYPES OF INDETERMINATE FORMS
▹ L-HOSPITAL’S RULE
▹ LIST OF COMMON INDETERMINATE FORMS

3. 3
-HISTORY-
The term was originally
introduced by Cauchy's
student Moigno (also known as
François-Napoléon-Marie Moigno)
in the middle of the 19th century.

4. INDETERMINATE FORMS
 What are indeterminate forms?
In calculus and other branches of mathematical
analysis, limits involving an algebraic combination of
functions in an independent variable may often be
evaluated by replacing these functions by their limits.
If the expression obtained after this substitution does
not give enough information to determine the original
limit, it is said to take on an indeterminate form.
4

5. TYPES OF
INDETERMINATE
FORMS
5

6. 6
Types of indeterminate forms
 There are seven types of indeterminate forms:
0
0
0
0
0
0
1


 
  

1.
2.
3.
4.
5.
6.
7.

7. L-HOSPITAL’S RULE
7
L’Hospital's rule is a general
method for evaluating the
indeterminate forms 0/0 &
∞/∞. This rule states that…
(under appropriate
conditions)
( ) '( )
( ) '( )
x c x c
f x f x
g x g x
lim lim
 

*where f’(x)and g’(x) are thederivatives of f(x) and g(x).

8. 8
0
:
0
Rulestoevaluate form
1. Check whether the limit is an indeterminate form. If it is not, then
we cannot apply L’ Hospital's rule.
2. Differentiate f(x) and g(x) separately.
3. If g’(a) ≠ 0, then the limit will exist. It may be finite, +∞ or -∞. If
g’(a)=0 then follow rule 4.
4. Differentiate f’(x) & g’(x) separately.
5. Continue the process till required value is reached.

9. “
▹ In this form you can
directly apply the L-
HOSPITAL’S RULE in the
equation.
0
1.
0
form
9
( ) '( )
( ) '( )
x c x c
f x f x
g x g x
lim lim
 

_____________________________________________

10. “
▹ Same as the previous one,
you can directly apply the L-
Hospital’s rule in the
equation.
10
2. form


( ) '( )
( ) '( )
x c x c
f x f x
g x g x
lim lim
 

_____________________________________________

11. 11
Example
0
0
form form


5 2
lim
7 3
x
x
Find
x



Solution:
5 2
lim
7 3
5 2
lim
7 3
5 2
lim
7 3
x
x
x
x
form
x
x
x
x
x
x
x x
x
x x



 
 
   
 
 






2
5
lim
3
7
5 0
7 0
5
7
x
x
x









12. “
12
3. 0 form

 Limit of the form
are called indeterminate form of the
type.
 If we write f(x) g(x) = f(x) / [1/g(x)], then
the limit becomes of the form .
 Therefore, this can be evaluated by
using L-Hospital’s rule.
lim ( ) 0,lim ( )
x c x c
f x g x
 
  
0
0
0
_____________________________________________

13. 13
Example
2
lim sin .
x
Consider x
x

 
 
  
 
 
 
2
sin
lim
1
x
x
x

 
 
 
 
 
 

 
 
 
   
2
2
2
sin
lim
1
2 2
cos
lim
1
2
lim 2cos
2cos 2 2cos 0 2
x
x
x
x
x
x x
x
x



 
 
 
 
 
 

 
 
 
  

  
  


 
  
 
   
Solution:
 First flip the x to denominator
*Now this limit has the form of 0/0. (We have simply
taken the ∞, and transformed it into a 0
In the denominator.) Therefore, this limit can be
done with L-Hospital’s rule.

14. “
14
4. form
 
 Limit of the form
are called indeterminate form of the
type.
 If we write
then, the limit becomes of the form 0/0
and can be evaluated by using the L-
---Hospital’s rule.
lim ( ) ,lim ( )
x c x c
f x g x
 
   
  
1 ( ) 1 ( )
lim( ( ) ( )) lim
1 ( ( ) ( ))
x c x c
g x f x
f x g x
f x g x
 

 
_____________________________________________

15. 15
Example

16. “
16
0
5. 0 form
 Limit of the form
are called indeterminate form of the
type.
 If we write
then, the limit becomes of the form 0/0
and can be evaluated by using the L-
---Hospital’s rule.
lim ( ) 0 ,lim ( ) 0
x c x c
f x g x

 
 
( ) ( )
lim ( ) explim
1 ln ( )
g x
x c x c
g x
f x
f x
 

_____________________________________________
0
0

17. 17
Example
0
lim .
x
x
Find x


Solution:
This is an indeterminate form of the type
Let
0
0
ln ln ln
x x
y x y x x x
   
2
0 0 0 0
0
0
ln 1
lim ln lim lim lim( ) 0.
1 1
, lim 1
x x x x
x
x
x x
y x
x x
Thus x e
   

   

     

 

18. “
18
6. 1 form

 Limit of the form
are called indeterminate form of the
type.
 If we write
then, the limit becomes of the form 0/0
and can be evaluated by using the L-
---Hospital’s rule.
lim ( ) 1,lim ( )
x c x c
f x g x
 
  
( ) ( )
lim ( ) explim
1 ( )
g x
x c x c
f x
f x
g x
 

_____________________________________________
1

19. 19
Example
1
0
lim (cos )x
x
Find x


Solution:
This is an indeterminate form of the type
Let
1
1
(cos )x
y x

 
 
1
0 0 0
1
0
0
ln(cos )
ln ln cos
ln(cos )
lim ln lim lim( tan ) 0.
, lim cos 1.
x
x x x
x
x
x
y x
x
x
y x
x
Thus x e
  

  

 
  
 
 
    
 

20. “
20
 Limit of the form
are called indeterminate form of the
type.
 If we write
then, the limit becomes of the form 0/0
and can be evaluated by using the L-
---Hospital’s rule.
lim ( ) ,lim ( ) 0
x c x c
f x g x
 
  
_____________________________________________
0
7. form

0

( ) ( )
lim ( ) explim
1 ( )
g x
x c x c
f x
f x
g x
 


21. 21
Example
2
lim( 1)
x x
x
Find e



Solution:
This is an indeterminate form of the type
Let
 
2
2
2
2ln( 1)
ln ln ( 1)
2
2
1
2ln( 1)
limln lim lim lim 2
1
,lim( 1) .
x
x x
x
x
x
x
x
x x x x
x x
x
e
y e
x
e
e
e
e
y
x e
Thus e e

   



   
   
 
 
 
   

   
     
 
0

2
( 1)
x x
y e

 

22. 22
 The following table lists the most common indeterminate forms, and the transformations for applying l'Hôpital's rule.

23. 23
THANKS !!
We have reached the end of the presentation.!!!