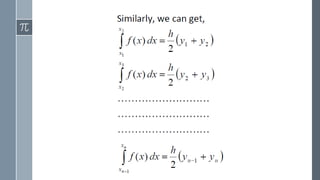This document discusses various applications of interpolation in computer science and engineering. It describes interpolation as a method of constructing new data points within the range of a known discrete data set. Some examples of interpolation applications mentioned include estimating population values, image processing through transformations like resizing and rotation, zooming digital images using different interpolation functions, and ray tracing in computer graphics. Numerical integration techniques like the trapezoidal rule, Simpson's rule, and Romberg's method are also briefly covered.

1. Application of
interpolation in CSE
4staR
@tanvir

2. In the mathematical field of numerical analysis, interpolation is a method
of constructing new data points within the range of a discrete set of
known data points.
What is Interpolation?

3. If we are find out the population of Dhaka in 1990 when we know the
population of Bangladesh in the year 1987, 1992, 1997, 2002,2007
and so on. i.e. the figure of population are available for 1987, 1992,
1997, 2002,2007 etc., then the process of finding the population of
1990 is known as interpolation
Example

5. Applications to image processing
Types:
 Rigid transformations
 Nonlinear transformations
One important application interpolation is the rigid transformation of images. By
rigid transformation we mean a linear transformation of the pixel coordinates.
.
Among rigid transformations, we find the subclass of affine transformations. Here
we use matlab for resizing, rotation and shear. To do this, we define a 3x3 matrix
of the form

7. An example of nonlinear transformation 5_3 to make a function with-
Input: an intensity image, a center point (x0,y0), a deformation parameter
d.
Output: The transformed cropped image matrix.

8. Zooming Digital Images using Interpolation
Techniques
Image processing for low resolution digital images ( mobile phones with low resolution
camera etc.) is very challenging problems. It is because of the errors due to quantization
and sampling. In particularly, zooming of such images is very complicated. For zooming,
the process of re-sampling is normally employed. Therefore, we use interpolation
functions on zooming low resolution images. For this purpose, ideally, an ideal low-pass
filter is preferred. Therefore, four interpolation functions-nearest neighbor, linear, cubic B-
spline and high-resolution cubic spline with edge enhancement is used.

9. Interpolation over Light Fields with Applications in
Computer Graphics
For this we present a data structure, called a ray interpolant tree, or RI tree. which
stores a discrete set of directed lines in 3-space, each represented as a point in 4-
space. Each directed line is associated with some small number of continuous
geometric attributes. We illustrate the practical value of the RI-tree in two applications
from computer graphics: ray tracing and volume visualization. In particular, given
objects defined by smooth curved surfaces, the RI-tree can produce high-quality
renderings significantly faster than standard methods.

10. The Lagrange Interpolation Polynomial for Neural
Network Learning
One of the methods used to find this polynomial is called the Lagrange
method of interpolation.The Lagrange interpolation method was used in a
new neural network learning by develops the weighting calculation in the
back propagation training. This proposed developing decrease the learning
time with best classification operation results. Also, the Langrage
interpolation polynomial was used to process the image pixels and remove
the noise the image. This interpolation gives the effective processing in
removing the noise and error in the image layers.

11. DISADVANTAGES.
1.Cannot estimate above maximum or below minimum values.
2.Not very good for peaks or mountainous areas

12. NUMERICAL INTEGRATION
4staR

13. Numerical integration is the approximate computation of integral using numerical
techniques.
Numerical integration is the process by which we can find the value of definite integral
𝑎
𝑏
𝑓 𝑥 𝑑𝑥 numerically by using some well-established formulae or rules.
What is Numerical integration?

14.  Trapezoidal Rule
 Simpson’s 1/3 Rule
 Simpson’s 3/8 Rule
 Boole’s Rule
 Weddle’s Rule
 Romberg’s Integration Rule etc.
The developed approximating methods are:

15. General Integration Formula

16. Simpson’s
𝟏
𝟑
Rule

17. General integration formula:
Setting n =2 in above equation we have the interval [ 𝑥0, 𝑥2] and neglecting the higher
order differences more than two, we get

21. Similarly, we can write,

22. By the rule of definite integral:

24. Trapezoidal Rule

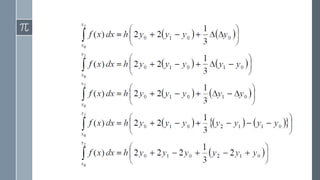
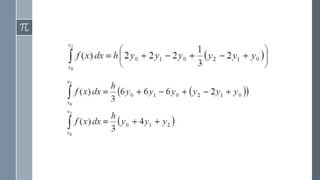
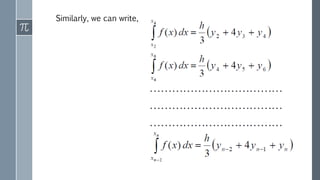
25. General integration formula:
Setting n = 1 in above equation we have the interval [ 𝑥0, 𝑥1]and neglecting the
higher order differences more than one, we get

28. By the rule of definite integral, we can write:

30. Any
Question?

31. Thank
you