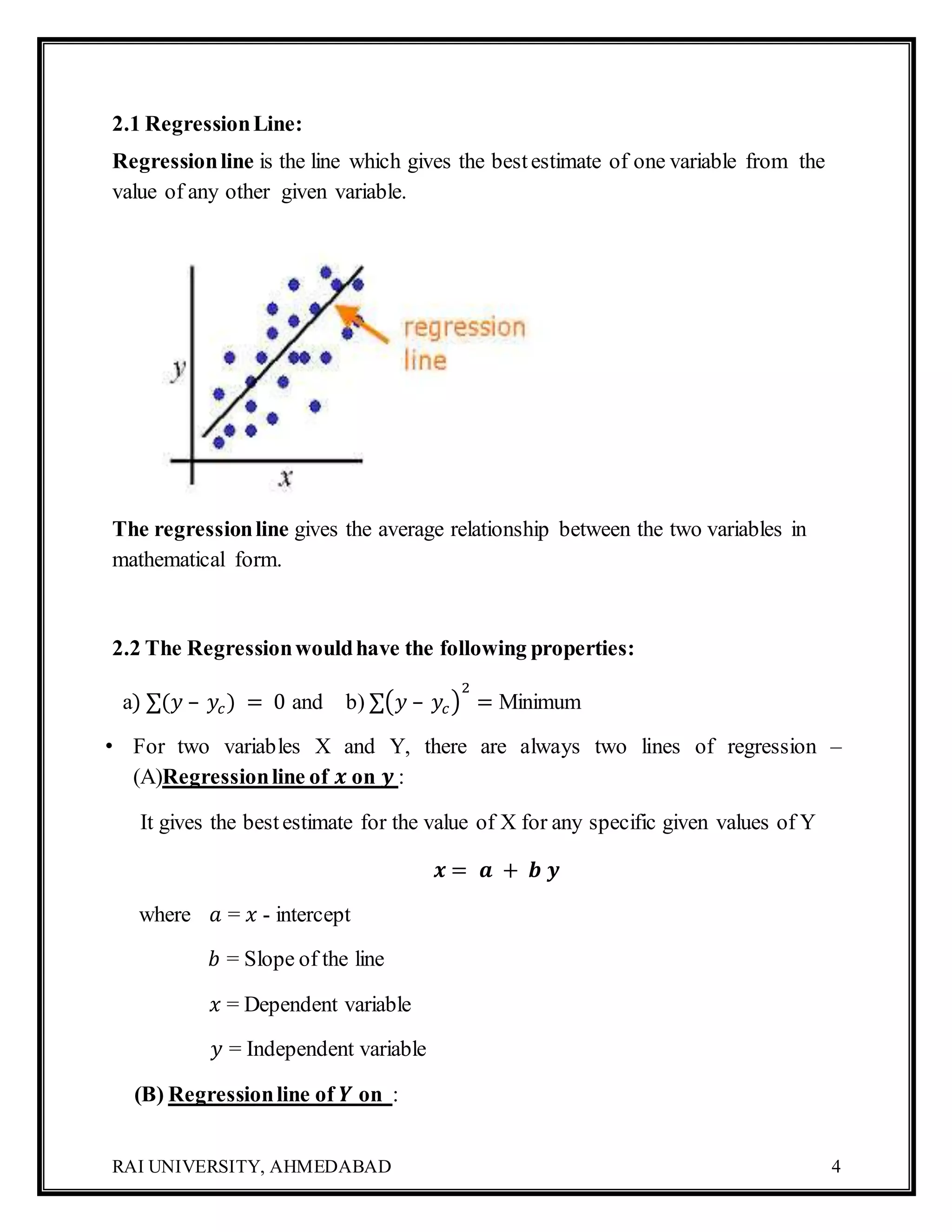
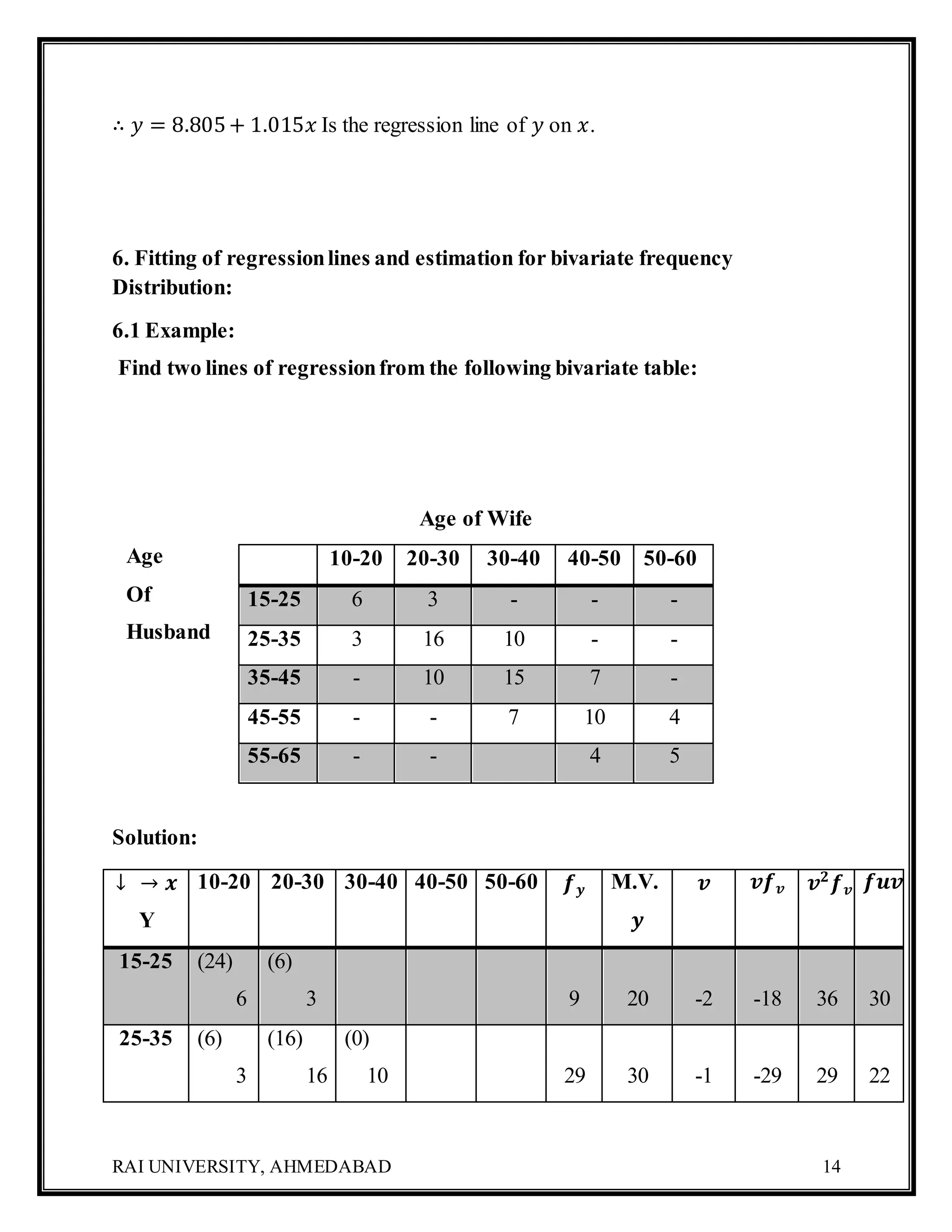
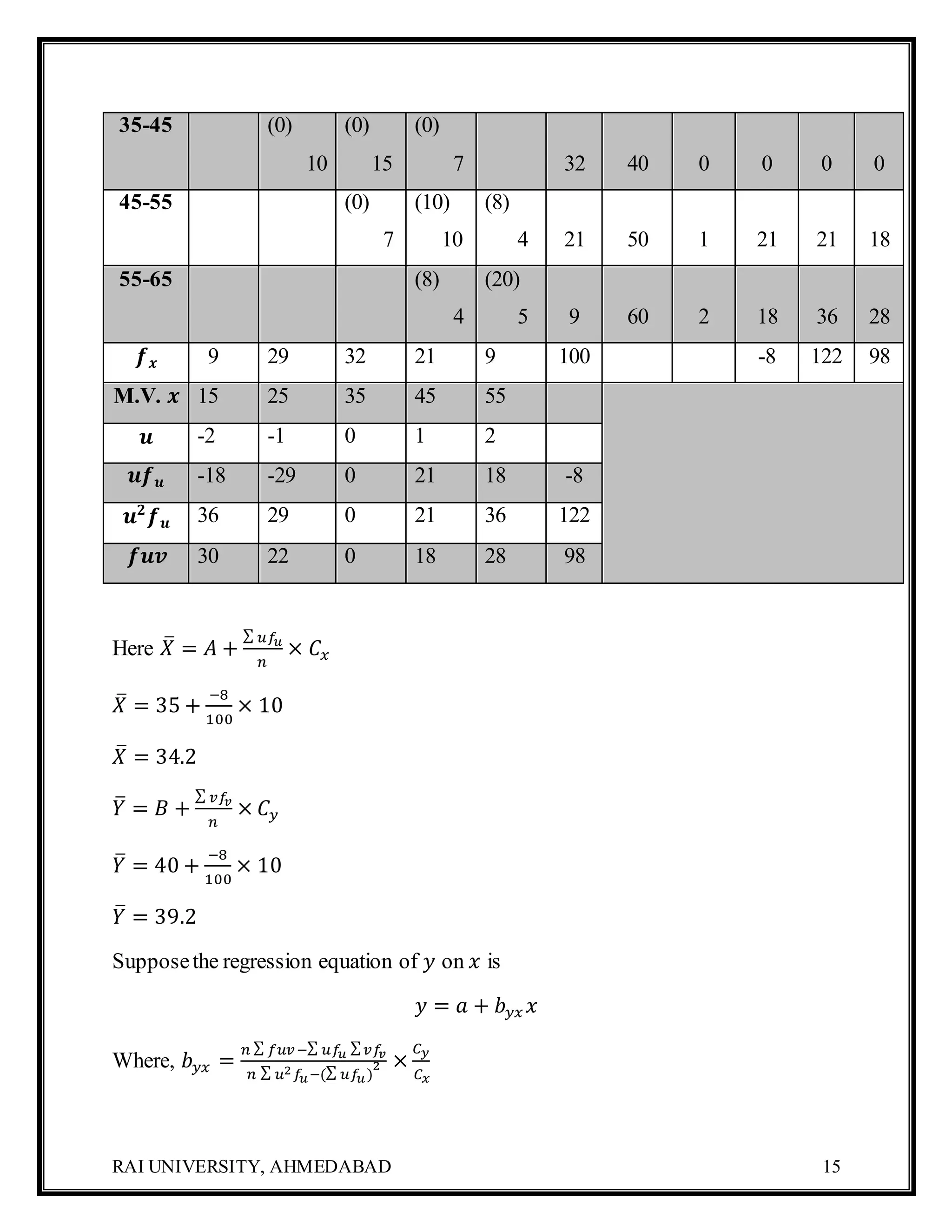
The document focuses on regression analysis, detailing its definition, significance, and various properties related to regression lines and coefficients. It differentiates between regression and correlation, provides formulas for regression equations, and includes examples demonstrating the calculation of regression lines and estimation for bivariate frequency distribution. Additionally, it covers the advantages and limitations of regression analysis in predicting values based on the correlation of two variables.