This document provides an in-depth explanation of simple linear regression (SLR), including its mathematical formulation, estimation of model parameters, significance testing, and goodness of fit. It explains how to derive the model parameters β0 and β1 using sample data, the principle of least squares, and describes the processes for testing the significance of these parameters. Additionally, it covers the coefficient of determination (r²) as a measure of the model's explanatory power.

1. Simple Linear Regression
The simplest of all machine learning techniques is “Simple Linear Regression”. In this
blog, I will explain in detail the mathematical formulation of Simple Linear Regression
(SLR) and how to:
• Estimate model parameters
• Test significance of parameters
• Test goodness of the model fit
Let me begin with the definition of SLR. A simple linear regression is a statistical
technique used to investigate the relationship between two variables in a non-
deterministic fashion. In general, it is used to estimate an unknown variable (aka
dependent variable) by determining its relationship with a known variable (aka
independent variable).
Model Formulation
An SLR model can be generalized as:
𝑌 = 𝛽0 + 𝛽1 𝑥 + 𝜀
where, Y – dependent variable
x – independent variable
ε – random error [we assume ε ~ N(0, σ2
), homogenous and uncorrelated]
β0 – intercept (value of Y, when x = 0)
β1 – slope (change in Y per unit change in x)
An SLR model has 2 components,
• Deterministic (β0 + β1x)
• Random / Non-deterministic (ε)
This random error (ε) characterizes the linear regression model.

2. The regression model, 𝑌𝑖 = 𝛽0 + 𝛽1 𝑥𝑖 + 𝜀𝑖 implies that the responses Yi comes from a
normal probability distribution whose means are
𝐸(𝑌|𝑥) = 𝛽0 + 𝛽1 𝑥
And variances are σ2
(the same for all levels of x). Also, any two responses Yi and Yj are
uncorrelated.
Estimating Model Parameters
To determine the values of Yi for each xi, the values of β0 and β1 are not known. Instead,
we have some sample data available.
We have to estimate β0 and β1 of the true regression line from the available data, from
which we get
𝑌𝑖 = 𝛽0 + 𝛽1 𝑥𝑖
and estimate the errors,
𝜀𝑖 = 𝑌𝑖 − 𝑌̂𝑖 = 𝑌𝑖 − (𝛽0 + 𝛽1 𝑥𝑖)
Where, 𝑌̂ is the estimated value of 𝑌𝑖
In the following figure below, describing a scatter plot of x vs Y
Which of these lines best fits the data and can be
assumed as the true regression line?
To find the best fit line, we use the “Principle of Least Squares”, which states that the
best fit line is the one having the smallest sum of squares of errors.
(Sum of squares of errors, 𝑆𝑆𝐸 = ∑ 𝜀𝑖
2𝑛
𝑖=1 = ∑ (𝑌𝑖 − 𝑌̂𝑖)2𝑛
𝑖=1 )

3. Thus, to obtain β0 and β1 of the best fit line
𝑌𝑖 = 𝛽0 + 𝛽1 𝑥𝑖
we minimize,
𝑓( 𝛽0, 𝛽1) = ∑ 𝜀𝑖
2𝑛
𝑖=1 = ∑ (𝑌𝑖 − 𝑌̂𝑖)2𝑛
𝑖=1 = ∑ (𝑌𝑖 − 𝛽0 − 𝛽1 𝑥𝑖)2𝑛
𝑖=1 …(1)
To find the minimum of equation (1), partially differentiate 𝑓( 𝛽0, 𝛽1) with respect to β0
and β1 and equate to zero.
𝜕𝑓
𝜕𝑥
= −2 ∑( 𝑌𝑖 − 𝛽0 − 𝛽1 𝑥𝑖) = 0 … (2)
⇒ 𝛽0 𝑛 + 𝛽1 ∑ 𝑥𝑖 = ∑ 𝑦𝑖 … (3)
𝜕𝑓
𝜕𝑥
= −2 ∑( 𝑌𝑖 − 𝛽0 − 𝛽1 𝑥𝑖) = 0 … (4)
⇒ 𝛽0 ∑ 𝑥𝑖 + 𝛽1 ∑ 𝑥𝑖
2
= ∑ 𝑥𝑖 𝑦𝑖 … (5)
Solve equations (3) and (5) to obtain β0 and β1.
Equations (3) and (5) in matrix form:
[
𝑛 ∑ 𝑥𝑖
∑ 𝑥𝑖 ∑ 𝑥𝑖
2] . [
𝛽0
𝛽1
] = [
∑ 𝑥𝑖
∑ 𝑥𝑖 𝑌𝑖
] … (6)
[
𝛽0
𝛽1
] = [
𝑛 ∑ 𝑥𝑖
∑ 𝑥𝑖 ∑ 𝑥𝑖
2]
−1
. [
∑ 𝑥𝑖
∑ 𝑥𝑖 𝑌𝑖
] … (7)
[
𝛽0
𝛽1
] =
1
𝑛 ∑ 𝑥 𝑖
2− (∑ 𝑥 𝑖)2
[
∑ 𝑥𝑖
2
∑ 𝑌𝑖 − ∑ 𝑥𝑖 ∑ 𝑥𝑖 𝑌𝑖
𝑛 ∑ 𝑥𝑖 𝑌𝑖 − ∑ 𝑥𝑖 ∑ 𝑥𝑖 𝑌𝑖
] … (8)
From equation (8),
𝛽1 =
∑ 𝑥 𝑖 𝑌 𝑖−
∑ 𝑥 𝑖 ∑ 𝑌 𝑖
𝑛
∑ 𝑥 𝑖
2−
(∑ 𝑥 𝑖)2
𝑛
… (9)
𝛽1 =
∑(𝑥 𝑖−𝑥̅ 𝑖)(𝑌 𝑖−𝑌̅ 𝑖)
∑(𝑥 𝑖−𝑥̅ 𝑖)2
=
𝑆 𝑥𝑦
𝑆 𝑥𝑥
… (10)
𝛽0 = 𝑌̅ − 𝛽1 𝑥̅ … (11)
where, 𝑥̅ =
∑ 𝑥 𝑖
𝑛
𝑌̅ =
∑ 𝑌 𝑖
𝑛

4. 𝑆 𝑥𝑦 = ∑(𝑥𝑖 − 𝑥̅𝑖)(𝑌𝑖 − 𝑌̅𝑖)
𝑆 𝑥𝑥 = ∑( 𝑥𝑖 − 𝑥̅𝑖)2
We can thus predict the value of the dependent variable Yi by substituting the values of
𝛽0 and 𝛽1 obtained from equation (10) and (11) in the equation:
𝑌𝑖 = 𝛽0 + 𝛽1 𝑥𝑖
Testing Significance of Model Parameters - 𝜷 𝟎 and 𝜷 𝟏
Distribution of 𝜷 𝟏
σ2
determines the amount of variability inherent in the regression model. As the equation
of true line is unknown, an estimate is based on the extent, the sample observation
deviates from the estimated line. This fitted line falls on the mean of the sample data, thus
the standard deviation can be estimated using this line
𝜎2
=
𝑆𝑆𝐸
𝑛 − 2
=
∑ 𝜀𝑖
𝑛
𝑖=1
𝑛 − 2
Since each 𝜀𝑖 is normally distributed, each Yi is also normal. And since 𝛽1 is a linear
function of each independent variable Yi, we have:
• 𝛽1is normally distributed
• 𝐸( 𝛽1) = 𝛽1
• 𝑉𝑎𝑟( 𝛽1) = 𝜎𝛽1
2
=
𝜎2
∑(𝑥 𝑖−𝑥̅)2
=
𝜎2
𝑆 𝑥𝑥
Hence,
𝛽1 ~ 𝑁(𝛽1, 𝜎2
𝑆 𝑥𝑥)⁄
𝑠𝑒( 𝛽1) = √
𝜎2
𝑆 𝑥𝑥

5. The assumptions of SLR model states that:
𝜷 𝟏− 𝜷 𝟏
𝟎
√𝝈 𝜷 𝟏
𝟐
~ 𝑵( 𝟎, 𝟏)
Thus, the standardized variable:
𝑇 =
𝛽1 − 𝛽1
0
𝜎 √ 𝑆 𝑥𝑥⁄
=
𝛽1 − 𝛽1
0
𝑠𝑒( 𝛽1)
has a t – distribution with (n-2) degrees of freedom.
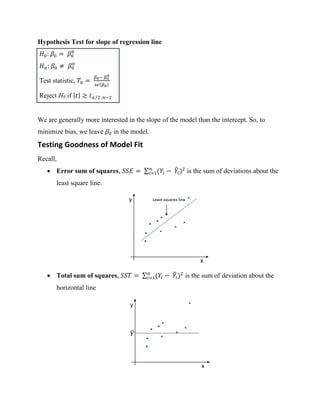
Hypothesis Test for slope of regression line:
𝐻0: 𝛽1 = 𝛽1
0
𝐻 𝛼: 𝛽1 ≠ 𝛽1
0
Test statistic, 𝑇0 =
𝛽1− 𝛽1
0
𝑠𝑒(𝛽1)
Reject H0 if | 𝑡| ≥ 𝑡 𝛼 2 ,𝑛−2⁄
The most general assumption is 𝐻0: 𝛽1 = 0 versus 𝐻 𝛼: 𝛽1 ≠ 0
In this case, rejecting H0 implies that there is no significant relation between x and Y.
Distribution of 𝜷 𝟎
Using a similar approach as that of 𝛽1, we get,
𝛽0 ~ 𝑁(𝛽0, 𝜎𝛽0
2
)
where, 𝜎𝛽0
2
= 𝜎2
[
1
𝑛
+
𝑥̅2
∑(𝑥 𝑖− 𝑥̅)2
] = 𝜎2
[
1
𝑛
+
𝑥̅2
𝑆 𝑥𝑥
]
Also,
𝜷 𝟎− 𝜷 𝟎
𝟎
√𝝈 𝜷 𝟎
𝟐
~ 𝑵( 𝟎, 𝟏)
Thus, the standardized variable,
𝑇 =
𝛽0 − 𝛽0
0
𝑠𝑒( 𝛽0)
has a t – distribution with (n-2) degrees of freedom

6. Hypothesis Test for slope of regression line
𝐻0: 𝛽0 = 𝛽0
0
𝐻 𝛼: 𝛽0 ≠ 𝛽0
0
Test statistic, 𝑇0 =
𝛽0− 𝛽0
0
𝑠𝑒(𝛽0)
Reject H0 if | 𝑡| ≥ 𝑡 𝛼 2 ,𝑛−2⁄
We are generally more interested in the slope of the model than the intercept. So, to
minimize bias, we leave 𝛽0 in the model.
Testing Goodness of Model Fit
Recall,
• Error sum of squares, 𝑆𝑆𝐸 = ∑ (𝑌𝑖 − 𝑌̂𝑖)2𝑛
𝑖=1 is the sum of deviations about the
least square line.
• Total sum of squares, 𝑆𝑆𝑇 = ∑ (𝑌𝑖 − 𝑌̅𝑖)2𝑛
𝑖=1 is the sum of deviation about the
horizontal line

7. Note that, SSE < SST.
SSE / SST represents the proportion of variation that cannot be explained by the
Simple Linear Regression.
The Coefficient of Determination, denoted by R2
is given by
𝑅2
= 1 −
𝑆𝑆𝐸
𝑆𝑆𝑇
R2
represents the proportion of variation explained by the Simple Linear
Regression.
❖ Higher the value of R2
, better is the model in explaining the variation in Y.