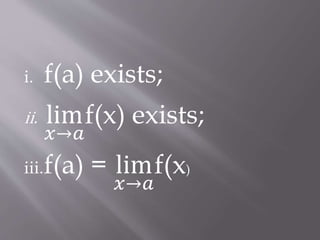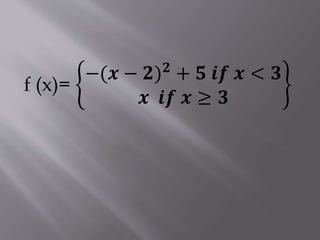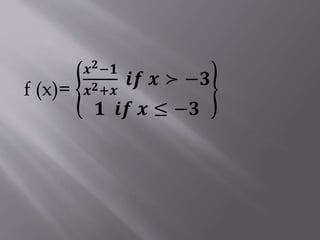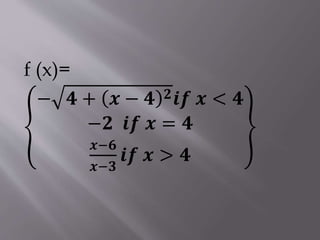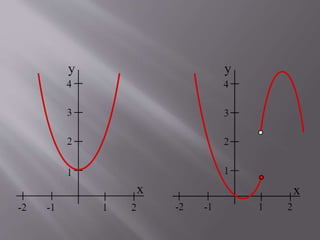
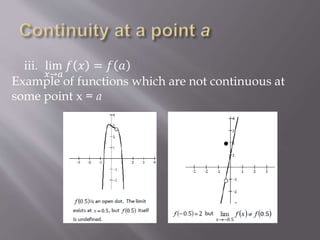
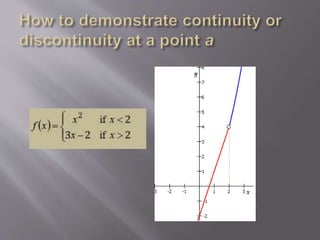
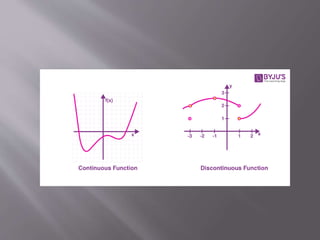
1. The document discusses limits, continuous functions, and discontinuous functions. It provides examples of functions that are continuous or discontinuous at various values of x. 2. A function is continuous at a point x=a if f(a) exists, the limit of f(x) as x approaches a exists, and the limit equals f(a). If any of these conditions fail, the function is discontinuous at x=a. 3. There are three types of discontinuities: removable, jump, and infinite. The document provides examples and graphical representations of continuous and discontinuous functions.

3. Evaluate the following Limits
1. lim
𝑥→9
𝑥2
2. lim
𝑥→4
6𝑥
𝑥−2
3. lim
𝑥→2
𝑥4−16
𝑥−2
4. lim
𝑥→−2
1
2
+
1
𝑥
𝑥+2
5. lim
𝑥→3
1
𝑥2−
1
9
𝑥−3

4. Continuous functions, discontinuous
functions

5. A function is said to be continuous on
the interval when the function is
continuous at a number in that
interval. If c is a number in the
interval(a, b) and f is a function with
a domain containing the interval(a,b),
then f is said to be continuous at x = c
if all the following conditions are
satisfied:

6. i. f(a) exists;
ii. lim
𝑥→𝑎
f(x) exists;
iii.f(a) = lim
𝑥→𝑎
f(x)

7. If one or more of these
three conditions fails to
hold at a, the function f
is said to be
discontinuous at a.

8. Any polynomial function
is continuous at all real
numbers

9. Any rational functions is
continuous at any real
number that makes the
denominator nonzero.

10. Solution:
i. f (1)= 𝟒𝒙𝟐
+ 𝒙 − 𝟐
ii. lim
𝑥→1
𝟒𝒙𝟐
+ 𝒙 − 𝟐
iii. lim
𝑥→1
f(x) = f(1)
The function is continuous at x = 1

11. Solution:
i. f (0)=
𝒙𝟐−𝟗
𝒙−𝟑
ii. lim
𝑥→0
𝒙𝟐−𝟗
𝒙−𝟑
iii. lim
𝑥→0
f(x) = f(x)
The function is continuous at x = 0

12. Solution:
i. f (3)=
𝒙𝟐−𝟗
𝒙−𝟑
ii. lim
𝑥→3
𝒙𝟐−𝟗
𝒙−𝟑
iii. lim
𝑥→3
f(x) = f(x)
The three function are not satisfied.
The function is discontinuous at x = 3

13. Solution:
i. f (3)= −𝟐𝒙 + 𝟒
ii. lim
𝑥→3+
− 𝟐𝒙 + 𝟒
lim
𝑥→3−
(𝒙 − 𝟏)
iii. lim
𝑥→3
f(x) ≠ f(x)
The second condition is not satisfied at x = 3.
The function is discontinuous at x = 3

14. Solution:
i. f (-1)= 3
ii. lim
𝑥→−1+
+ (𝑥 + 1)
lim
𝑥→−1−
− (𝑥 + 1)
iii. lim
𝑥→−1
f(x) ≠ f(-1)
The function is discontinuous at x = -1

15. Solution:
i. f (2)= 4𝑥 − 2
ii. lim
𝑥→2+
(−2𝑥 + 5)
lim
𝑥→2−
(4𝑥 − 2)
iii. lim
𝑥→2+
f(x) ≠ lim
𝑥→2
f(x)
The function is discontinuous at x = 2

16. f (x)=
−(𝒙 − 𝟐)𝟐 + 𝟓 𝒊𝒇 𝒙 < 𝟑
𝒙 𝒊𝒇 𝒙 ≥ 𝟑

17. f (x)=
𝒙𝟐−𝟏
𝒙𝟐+𝒙
𝒊𝒇 𝒙 ≻ −𝟑
𝟏 𝒊𝒇 𝒙 ≤ −𝟑

18. f (x)=
− 𝟒 + 𝒙 − 𝟒 𝟐𝒊𝒇 𝒙 < 𝟒
−𝟐 𝒊𝒇 𝒙 = 𝟒
𝒙−𝟔
𝒙−𝟑
𝒊𝒇 𝒙 > 𝟒

19. g (x)=
−𝟓𝒙 + 𝟏𝟑 𝒊𝒇 𝒙 ≤ −𝟐
𝒙𝟐
+ 𝟒𝒙 + 𝟕 𝒊𝒇 𝒙 ≻ 𝟐

20. 1. f (x)=
𝒙𝟐 − 𝟒 𝒊𝒇 𝒙 < 𝟐
𝟒 𝒊𝒇 𝒙 = 𝟐
𝟒 − 𝒙𝟐𝒊𝒇𝒙 > 𝟐

21. 2. f (x)=
−𝒙 𝒊𝒇 𝒙 < 𝟎
𝟑
𝒙 + 𝟏𝒊𝒇 𝒙 ≥ 𝟎

22. 3. f (x)=
−𝟏 𝒊𝒇 𝒙 < 𝟎
𝟎 𝒊𝒇 𝒙 = 𝟎
𝒙𝒊𝒇 𝒙 > 𝟎

23. A removable discontinuity
if the limit of f(x) as x
approaches a exists, and not
equal to f(a).
lim
𝑥→𝑎
𝑓 𝑥 ≠ 𝑓(𝑥)

24. A jump discontinuity if the
limit of f(x) as x approaches to
a from the right is not equal to
the limit of f(x) as x
approaches to a from the left.
lim
𝑥→𝑎−
𝑓 𝑥 ≠ lim
𝑥→𝑎+
𝑓 𝑥

25. An Infinite discontinuity
at x = a, if the limit of f(x)
as x approaches to a is
infinite.
lim
𝑥→𝑎
𝑓 𝑥 = ∞

27. i. 𝑓 𝑎 exists.
The function is defined at a
The graph of the function contains 𝑎, 𝑓 𝑎
Examples of
functions not
continuous at
some x = a

28. ii. lim
𝑥→𝑎
𝑓 𝑥 exists
lim
𝑥→𝑎−
𝑓 𝑥 = lim
𝑥→𝑎+
𝑓 𝑥
Examples of
functions not
continuous at some
x = a

29. iii. lim
𝑥→𝑎
𝑓 𝑥 = 𝑓 𝑎
Example of functions which are not continuous at
some point x = a

30. A function which is not continuous at x = a is
discontinuous at that point.

32. Graphically, a function is continuous in an
interval when its graph has no “breaks” or
“jumps”.
A function is continuous when one can trace its
graph without lifting the pencil from the paper.

33. Continuous functions
Fig 1.8 𝑓 𝑥 = 𝑥

36. Function is not
continuous at x = 2

38. If a function has a removable discontinuity at a
point a, that discontinuity can be removed by
redefining the function to fit continuity, in
particular, by making lim
𝑥→𝑎
𝑓 𝑥 = 𝑓 𝑎

39. Sufficient conditions
for continuity Discontinuous at 𝑥 = 0,
𝑥 ≤ −1
It is undefined at these
values of x

40. Redefinition of a
new function

41. If the discontinuities cannot be removed, the
discontinuity is called essential discontinuity.
i. f(2) is undefined. The
function is discontinuous
at 2
ii. lim
𝑥→2
𝑓 𝑥 exists
iii. lim
𝑥→2
𝑓 𝑥 ≠ 𝑓 2

42. i. 𝑓 2 =?, f(2) does not exist
f is discontinuous at x = 2
ii. lim
𝑥→2−
𝑓 𝑥 = lim
𝑥→𝑎+
𝑓 𝑥 = 4
iii. lim
𝑥→2
𝑓 𝑥 ≠ 𝑓 2

43. Sufficient conditions
for continuity

44. Sufficient conditions
for continuity
Essentially discontinuous when 𝑥 ≤ −1. Why?
The discontinuity at x = 0 is removable because
lim
𝑥→0
𝑓 𝑥 = 2, 𝑖𝑡 𝑒𝑥𝑖𝑠𝑡𝑠

45. Redefined function