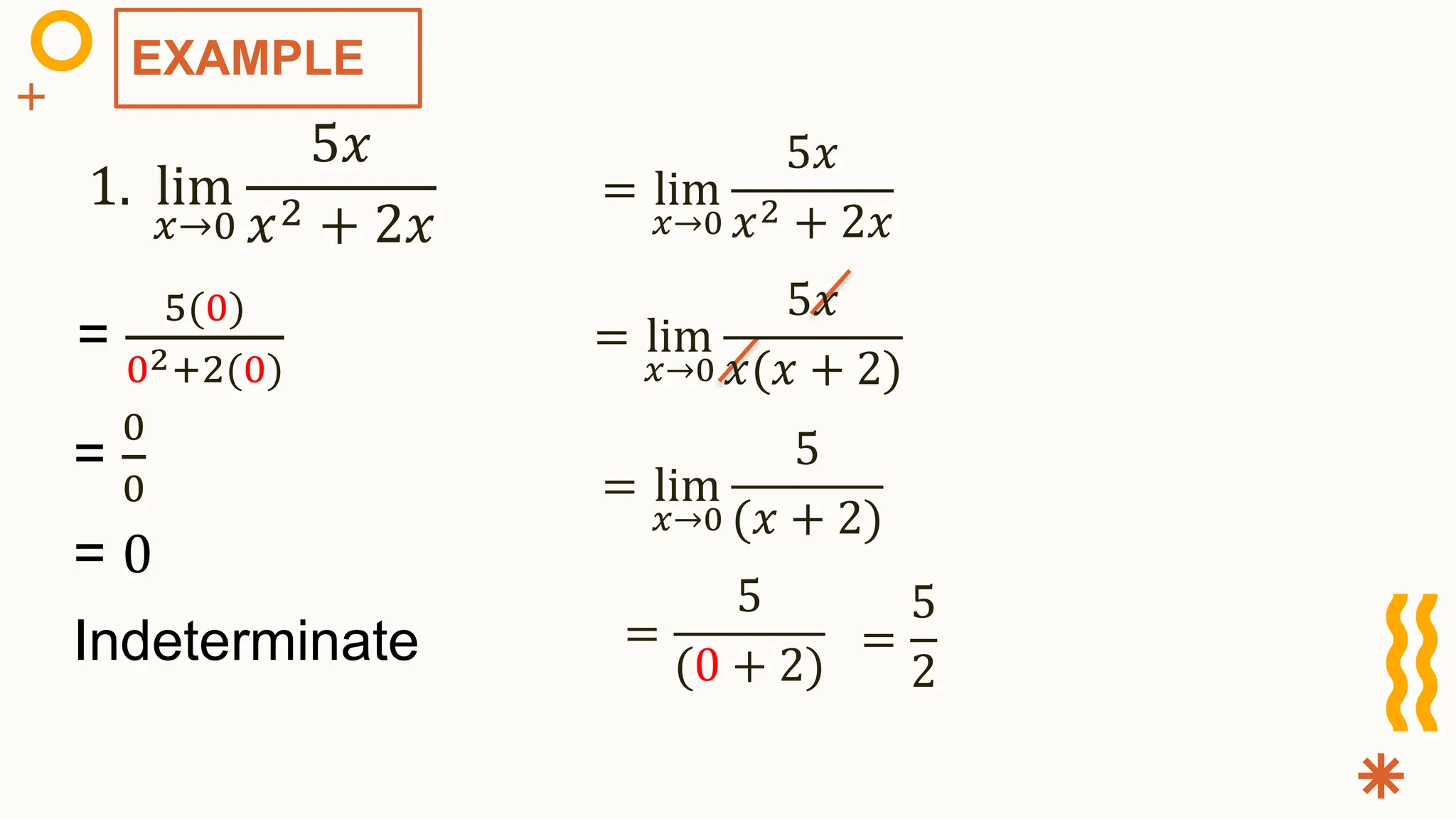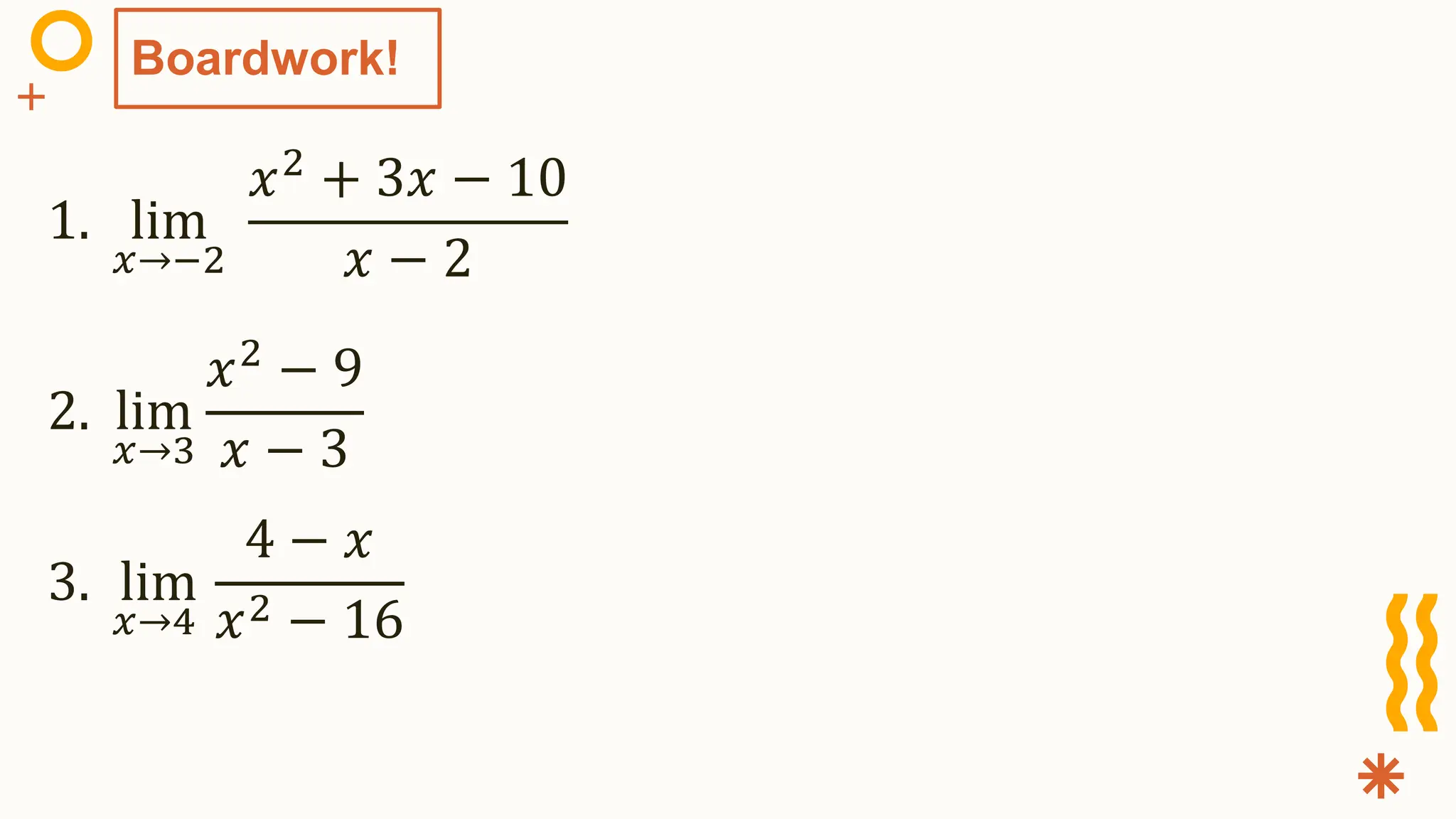This document provides an overview of calculating limits in calculus. It defines limits and describes techniques for determining limits, including: 1) Direct substitution of the limit value into the function. 2) Using identities, factoring, and rewriting in equivalent forms to simplify indeterminate forms like 0/0. 3) Approximating limits graphically or using tables of values when algebraic techniques don't yield the limit. The document explains these techniques through examples and provides practice problems for determining limits using different algebraic manipulations like factoring, conjugates, and trigonometric identities.

1. BASIC
CALCULUS

2. Unit I
Limits and Continuity

3. REVIEW

4. 1. f(x) = 1 + 3x
Complete the table of values below
given the functions.
x -3 -2 -1 0 1 2 3
f(x) -8 -5 -2 1 4 7 10

5. a. Describe the limit of a function using
correct notation.
b. Estimate the limit of a function or to
identify when the limit does not exist using
a table of values.
c. Estimate the limit of a function or to
identify when the limit does not exist using
OBJECTIVES

6. If f(x) becomes arbitrary close to a
unique number L as x approaches c from
either side, then the limit of f(x) as x
approaches c is L.
Read as:
“the limit of f(x), as x approaches c is L.”
LIMITS
lim
𝑥→𝐶
𝑓 𝑥 = 𝐿

7. The limit of a function 𝒍𝒊𝒎
𝒙→𝑪
𝒇 𝒙 = 𝑳 is
not the same as evaluating a function f(c)
because they are different in terms of
concept. The limit of a function gets its
value by providing inputs that approaches
the particular number while evaluating a
function is more like direct substitution
process.

8. One sided limit
is the value (L) as the x value gets
closer and closer to a certain value c from
one side only (either from the left or from
the right side). In symbols,
lim
𝑥→𝑐+
𝑓 𝑥 = 𝐿 lim
𝑥→𝑐−
𝑓 𝑥 = 𝐿

9. The notion of the limit of a function is
suggested by the question:
“What happens to f(x) as x gets nearer and
nearer to c (but x ≠ 𝐜)?
“Does f(x) approach some number L?”
The question implies that we have to find the
“limit of f(x) as x approaches c, or 𝐥𝐢𝐦
𝒙→𝑪
𝒇(𝒙)

10. A. Direct Substitution
(Try to evaluate function directly)
B. Asymptote (probably)
f(a) =
𝑏
0
where b is not zero
Example: lim
𝑥→1
1
𝑥−1
Calculating lim
𝑥→𝑎
𝑓 𝑥 = 𝐿
Inspect with a graph or
table to learn more about
the function at x = a

11. C. Limit found (probably)
f(a) = b where b is a real number
Example: lim
𝑥→3
𝑥2
= 32
= 9
D. Indeterminate form
f(a) =
𝟎
𝟎
Example: lim
𝑥→−1
𝑥2−𝒙 −𝟐
𝑥2−2𝑥−3

12. Rewriting limit in an equivalent form.
E. Factoring
Example: lim
𝑥→−1
𝑥2−𝒙 −𝟐
𝑥2−2𝑥−3
can be reduced to
lim
𝑥→−1
𝒙 −𝟐
𝑥−3
by factoring and cancelling.

13. F. Conjugates
Example: lim
𝑥→4
𝑥−2
𝑥 − 4
can be written as
lim
𝑥→4
1
𝑥 +2
using conjugates and cancelling.

14. G. Trig Identities
Example: lim
𝑥→0
sin(𝑥)
sin(2𝑥)
can be written as
lim
𝑥→0
1
2cos(𝑥)
using trigonometric identities.

15. H. Approximation
When all else fails, graphs and tables
can help approximate limits.

16. 1. lim
𝑥→2
3𝑥 − 2
Illustrating the Limit of a Function
x 1.9 1.99 1.999 2 2.001 2.01
f(x) 3.700 3.970 3.997 4.003 4.030
?
as x is approaching from the left and from the
right, f(x) is getting closer and closer to 4
∴ lim
𝑥→2
3𝑥 − 2 = 4

17. 2. lim
𝑥→2
1 + 3𝑥
as x is
approaching from
the left and from
the right, f(x) is
getting closer and
closer to 7
∴ 𝒍𝒊𝒎
𝒙→𝟐
𝟏 + 𝟑𝒙 = 7

18. 3. lim
𝑥→−1
(𝑥2
+ 1)
as x is
approaching from
the left and from
the right, f(x) is
getting closer and
closer to 2
∴ 𝒍𝒊𝒎
𝒙→𝟐
𝟏 + 𝟑𝒙 = 2

19. 4. lim
𝑥→2
(𝑥 + 3) solve for its limit when x approaches 2
as x is
approaching from
the left and from
the right, f(x) is
getting closer and
closer to 2
∴ 𝒍𝒊𝒎
𝒙→𝟐
𝒙 + 𝟑 = 2
x<2 f(x)
0
1
1.5
1.9
1.99
1.999
x>2 f(x)
4
3
2.5
2.1
2.01
2.001

20. 5. lim
𝑥→2
(4 + 𝑥) solve for its limit when x approaches 2
as x is
approaching from
the left and from
the right, f(x) is
getting closer and
closer to 2
∴ 𝒍𝒊𝒎
𝒙→𝟐
(𝟒 + 𝒙)=
x<2 f(x)
0
1.5
1.99
1.9999
x>2 f(x)
3
2.5
2.01
2.0001

21. A. Direct Substitution
(Try to evaluate function directly)
B. Asymptote (probably)
f(a) =
𝑏
0
where b is not zero
Example: lim
𝑥→1
1
𝑥−1
Techniques in Calculating Limits
lim
𝑥→𝑎
𝑓 𝑥 = 𝐿
Inspect with a graph or
table to learn more about
the function at x = a

22. A. Direct Substitution
(Try to evaluate function directly)
Different Techniques in Calculating
Limits

23. EXAMP
LE
1. lim
𝑤→1
(1 + 3
𝑤)(2 − 𝑤2
+ 3𝑤3
)
= (1 +
3
1)(2 − 12
+ 3(1)3
)
= (1 + 1)(2 − 1 + 3)
= (2)(4)
= 8
2. lim
𝑡→−2
𝑡2 − 1
𝑡2 + 3𝑡 − 1
=
(−2)2−1
(−2)2+3(−2)−1
=
4−1
4−6−1
=
3
−3
= −1

24. 3. lim
𝑧→2
(
2𝑧 + 𝑧2
𝑧2 + 4
)3
= (
2(2)+ (2)2
(2)2+4
)3
= (
4 + 4
4 + 4
)3
= (
8
8
)3
= 1
4. lim
𝑥→0
𝑥2 − 𝑥 − 2
𝑥3 + 6𝑥2 − 7𝑥 + 1
=
02−0 −2
03+6(0)2−7(0)+1
=
−2
1
= −2

25. Boardwork!
1. lim
𝑦→−2
4 − 3𝑦2 − 𝑦3
6 − 𝑦 − 𝑦2
2. lim
𝑥→−1
𝑥3 − 7𝑥2 + 14𝑥 − 8
2𝑥2 + 3𝑥 − 4
3. lim
𝑥→−1
𝑥2 + 3 − 2
𝑥2 + 1

26. Different Techniques in Calculating
Limits
Rewriting limit in an equivalent form.
B. Factoring
Example: lim
𝑥→−1
𝑥2−𝒙 −𝟐
𝑥2−2𝑥−3
can be reduced to
lim
𝑥→−1
𝒙 −𝟐
𝑥−3
by factoring and cancelling.

27. EXAMPLE
1. lim
𝑥→0
5𝑥
𝑥2 + 2𝑥
=
5(0)
02+2(0)
=
0
0
= 0
Indeterminate
= lim
𝑥→0
5𝑥
𝑥2 + 2𝑥
= lim
𝑥→0
5
(𝑥 + 2)
= lim
𝑥→0
5𝑥
𝑥(𝑥 + 2)
=
5
(0 + 2)
=
5
2

29. Boardwork!
1. lim
𝑥→−2
𝑥2 + 3𝑥 − 10
𝑥 − 2
2. lim
𝑥→3
𝑥2 − 9
𝑥 − 3
3. lim
𝑥→4
4 − 𝑥
𝑥2 − 16

30. Points to remember!
1. Substitute. Plug in the limit value into the
functuon. If the answer is a real number, that is a
limit.
2. If we substitute and we get indeterminate form
0/0, we need to simplify the fraction by

31. Different Techniques in
Calculating Limits
Conjugates
Example: lim
𝑥→4
𝑥−2
𝑥 − 4
can be written as
lim
𝑥→4
1
𝑥 +2
using conjugates and cancelling.

32. Limits that have sum or differences involving
square roots can be simplified by
conjugation