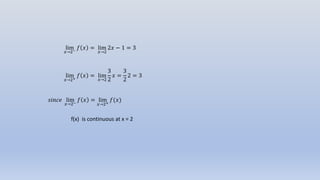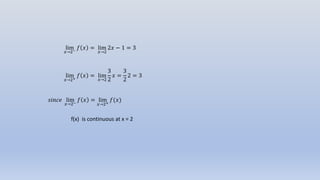
This document discusses continuity of functions. It provides examples of functions and examines whether they are continuous at various points. The key points are: 1) A function f(x) is continuous at a point a if the left-hand and right-hand limits of f(x) as x approaches a are equal to f(a). 2) An example function is examined and found to be continuous at x=2 because the left and right limits match the value of f(x) at x=2. 3) Another function is discontinuous at x=0 because the left and right limits do not match at that point.

1. Continuity of functions

2. A function f is said to be continuous at a, (a point in its domain) if
lim
𝑥→𝑎−
𝑓 𝑥 = lim
𝑥→𝑎+
𝑓 𝑥 = 𝑓(𝑎)
Question 1
Examine the following function for continuity
𝑓 𝑥 = 2𝑥 − 1 𝑖𝑓 𝑥 < 2
=
3
2
𝑥 𝑖𝑓 𝑥 ≥ 2

3. lim
𝑥→2−
𝑓 𝑥 = lim
𝑥→2
2𝑥 − 1 = 3
lim
𝑥→2+
𝑓 𝑥 = lim
𝑥→2
3
2
𝑥 =
3
2
2 = 3
𝑠𝑖𝑛𝑐𝑒 lim
𝑥→2−
𝑓 𝑥 = lim
𝑥→2+
𝑓(𝑥)
f(x) is continuous at x = 2

4. Question 2
𝑓 𝑥 =
𝑥
𝑥
, 𝑥 ≠ 0
= 0, x = 0
Is f continuous on R
lim
𝑋→0+
𝑓 𝑥 = lim
𝑥→0
𝑥
𝑥
= 1
lim
𝑥→0−
𝑓 𝑥 = lim
𝑥→0
𝑥
−𝑥
= −1

5. f is not continuous at 0
f is continuous everywhere else on R
Question 3
Find k, so that the function f defined by
f(x)= 𝑘𝑥2
, 𝑥 ≤ 2
= x – 3, x >2
may be continuous

6. lim
𝑥→2−
𝑓 𝑥 = lim
𝑥→2
𝑘𝑥2
= 4𝑘
lim
𝑥→2+
𝑓 𝑥 = lim
𝑥→2
𝑥 − 3 = −1
4k = -1
𝑘 = −
1
4

7. Question 4
Locate the points of discontinuity, if any, for the function f defined by
𝑓 𝑥 = 𝑥 + 3 𝑖𝑓 𝑥 ≤ −3
=-2x if -3< x <3
=6x +2, if x≥ 3
lim
𝑥→−3−
𝑓 𝑥 = lim
𝑥→−3
𝑥 +3 = −3 + 3 = 3 + 3 = 6

8. lim
𝑥→−3+
𝑓 𝑥 = lim
𝑥→−3
−2𝑥 = 6
lim
𝑥→−3+
𝑓 𝑥 = lim
𝑥→−3+
𝑓 𝑥
f is continuous at x = -3
lim
𝑥→3−
𝑓 𝑥 = lim
𝑥→3
−2𝑥 = −6

9. lim
𝑥→3+
𝑓 𝑥 = lim
𝑥→3
6𝑥 + 2 = 20
f is not continuous at x = 3
**************************
lim
𝑥→3−
𝑓 𝑥 ≠ lim
𝑥→3+
𝑓(𝑥)