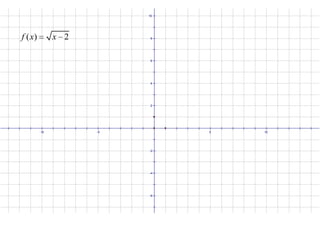
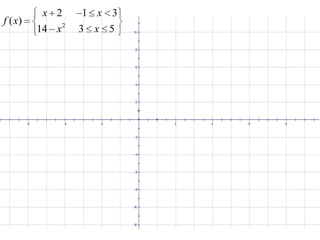
The document discusses continuity of functions. A function is continuous at a point c if the limit of the function as x approaches c exists and equals the value of the function at c. Polynomial and rational functions are continuous everywhere in their domains. A function can have discontinuities where it is not defined or where the limit does not equal the function value. Discontinuities are either removable, where redefining the function can make it continuous, or non-removable, where an asymptote prevents continuity. A function is continuous on a closed interval if it is continuous on the interior and the one-sided limits equal the function values at the endpoints.

1. 1.6 ContinuityGoal: to determine the continuity of functions.Continuity:Let c be a number in the interval (a, b) and let f be a function whose domain contains the interval (a, b). The function f is continuous at the point c if the following conditions are true: f(c) is defined.lim f(c) exists x−>clim f(x) = f(c) x−>cIf f is continuous at every point in the interval (a, b), then it is continuous on an open interval (a, b).

2. A polynomial function is continuous at every real number.A rational function is continuous at every number in its domain. Graph f(x) = x2 + x + 1, what would you say about its continuity?Continuous on (-∞, ∞)

3. Graph What about its continuity?Graph What about its continuity?If the function is defined over an interval in which c lies but f is not continuous at c, then the function is said to have a discontinuity at c.

4. How do we mathematically describe this? Think about how we describe domain We have a whole in our graph at x = 2 so if we use the same interval notation that we did with domain, we say:f(x) is continuous on (-∞, 2) U (2, ∞)This time we have an asymptote at x = 1 but again we use the same interval notation that we did with domain…f(x) is continuous on (-∞, 1) U (1, ∞)

5. Discontinuity:Removable: the function can be made continuous if it is redefined.From our previous example :this definition makes f(x) continuous Think of it this way, the hole is like a pothole, by redefining the domain we fill the hole with asphalt and “remove the hole”.

6. Discontinuity:Non-removable: the function cannot be made continuous if it is redefined. From our other previous example :x = 1 is the asymptote, not just a hole in the graph.Think of it this way, if you have an asymptote, it’s like an entire roadway, we can’t just move the entire roadway. This time the issue is “non-removable”

7. Continuity on a Closed Interval:Let f be defined on a closed interval [a, b]. If f is continuous on the open interval (a, b) and lim f(x) = f(a) x−>a+andlim f(x) = f(b)x−>b-then f is continuous on the closed interval [a, b]. Moreover, f is continuous from the right at a and continuous from the left at b.

8. Graph What about its continuity?Graph What about its continuity?

11. The Greatest Integer Function:

12. [[x]] = greatest integer less than or equal to x

13. This function allows for the truncation of decimal points.

14. Graph this function on your calculator: