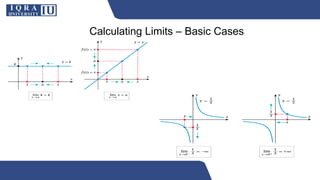
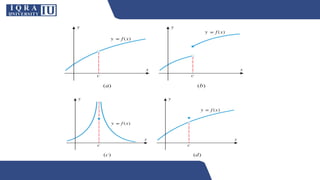
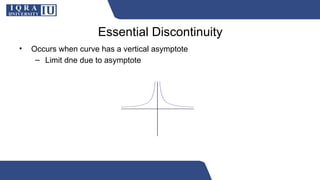
The document outlines the learning objectives and outcomes related to limits, continuity, and discontinuity in calculus and analytical geometry. It explains the fundamental concepts of limits, the types of continuity, and describes the four types of discontinuities. Additionally, it includes properties of continuous functions and factors affecting continuity in various mathematical expressions.

1. Welcome!!

2. Calculus and Analytical Geometry

3. Learning Objectives
Understanding of Limits
Continuity and Discontinuity in Functions
Learning Outcomes
Students will be able to define limits
Students will be able to discuss types of continuity and discontinuity and their plots

4. Two Basic Problems of Calculus
• The concept of a “limit” is the fundamental building block on which all calculus
concepts are based. Many of the ideas of calculus originated with the following
two geometric problems;
• The solution to both of these problems requires the use of limits
• Traditionally, that portion of calculus arising from the tangent line problem is called
differential calculus and that arising from the area problem is called integral
calculus

5. Limits
• In Mathematics, concept of limits is used to describe the “behaviour of a function”
as it’s input approaches or get close to a particular value.
• 1.1.1 (pg# 52)

6. Limits
1.1.2 (pg# 54)

7. Limits
1.1.2 (pg# 55)

8. Calculating Limits – Basic Cases

9. Calculating Limits – Algebra Rules

10. CONTINUITY
Intuitively, the graph of a function can be described as a “continuous curve” if it has
not breaks or holes.
The graph of a function has a break or hole if any of the following conditions occur:
• The function f is undefined at c
•The limit of f(x) does not exist as x approaches c
•The value of the function and the value of the limit at c are different.

12. Continuous Function

13. Example: Determine whether the following functions are continuous at x=-3.
Solution:
Observe that
•f(x) is not continuous at x=-3 since it’s undefined at x=-3,
•g(x) is not continuous at x=-3 since
•h(x) is continuous

14. Some properties of continuous functions

15. Types of Discontinuities
• There are 4 types of discontinuities
– Jump
– Point
– Essential
– Removable
• The first three are considered non removable

16. Jump Discontinuity
• Occurs when the curve breaks at a particular point and starts somewhere
else
– Right hand limit does not equal left hand limit

17. Point Discontinuity
• Occurs when the curve has a “hole” because the function has a value that is
off the curve at that point.
– Limit of f as x approaches x does not equal f(x)

18. Essential Discontinuity
• Occurs when curve has a vertical asymptote
– Limit dne due to asymptote

19. Removable Discontinuity
• Occurs when you have a rational expression with common factors in the
numerator and denominator. Because these factors can be cancelled, the
discontinuity is removable.

20. Places to test for continuity
• Rational Expression
– Values that make denominator = 0
• Piecewise Functions
– Changes in interval
• Absolute Value Functions
– Use piecewise definition and test changes in interval
• Step Functions
– Test jumps from 1 step to next.

21. Continuous Functions in their domains
• Polynomials
• Rational f(x)/g(x) if g(x) ≠0
• Radical
• trig functions

23. Thank you