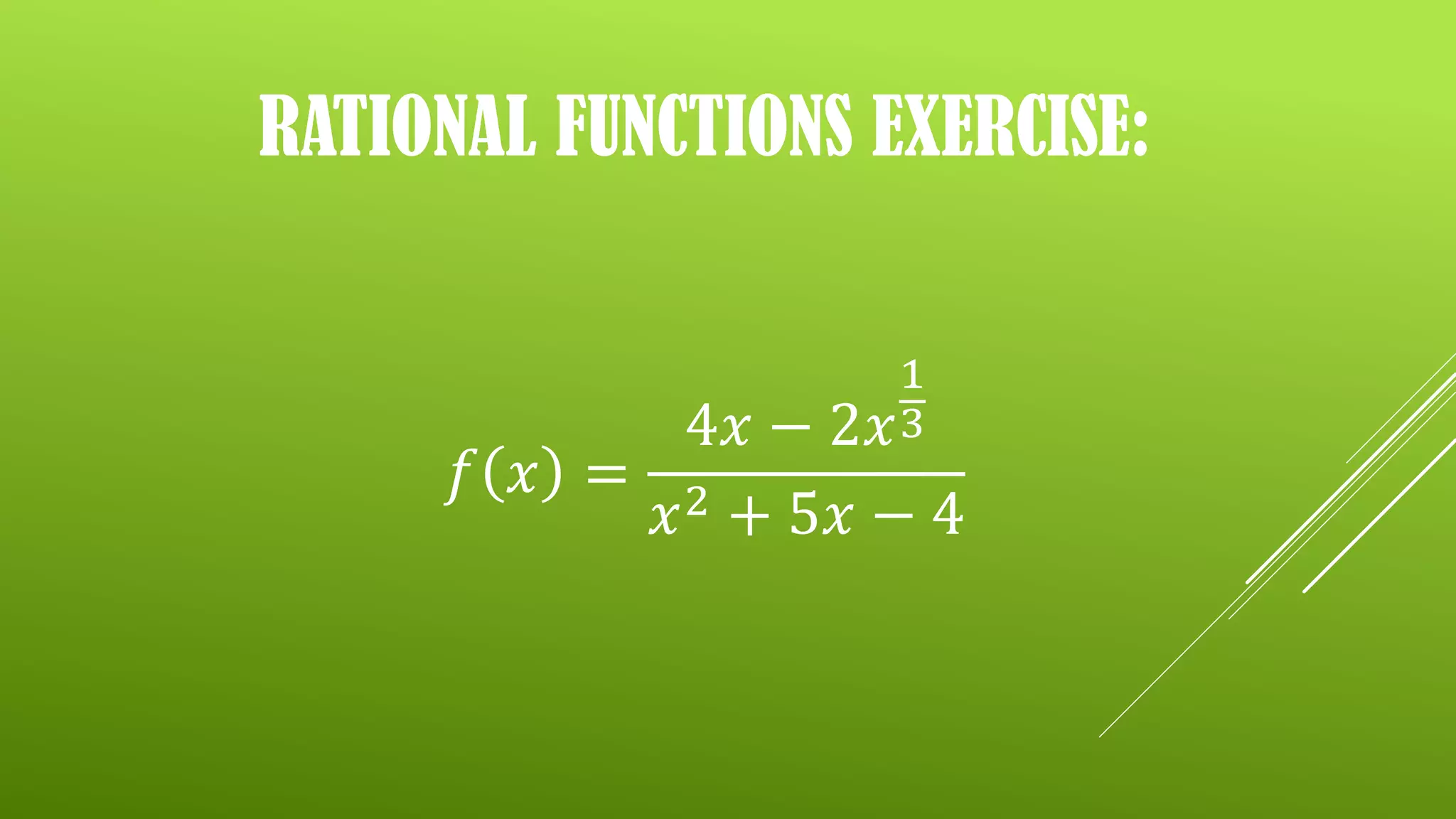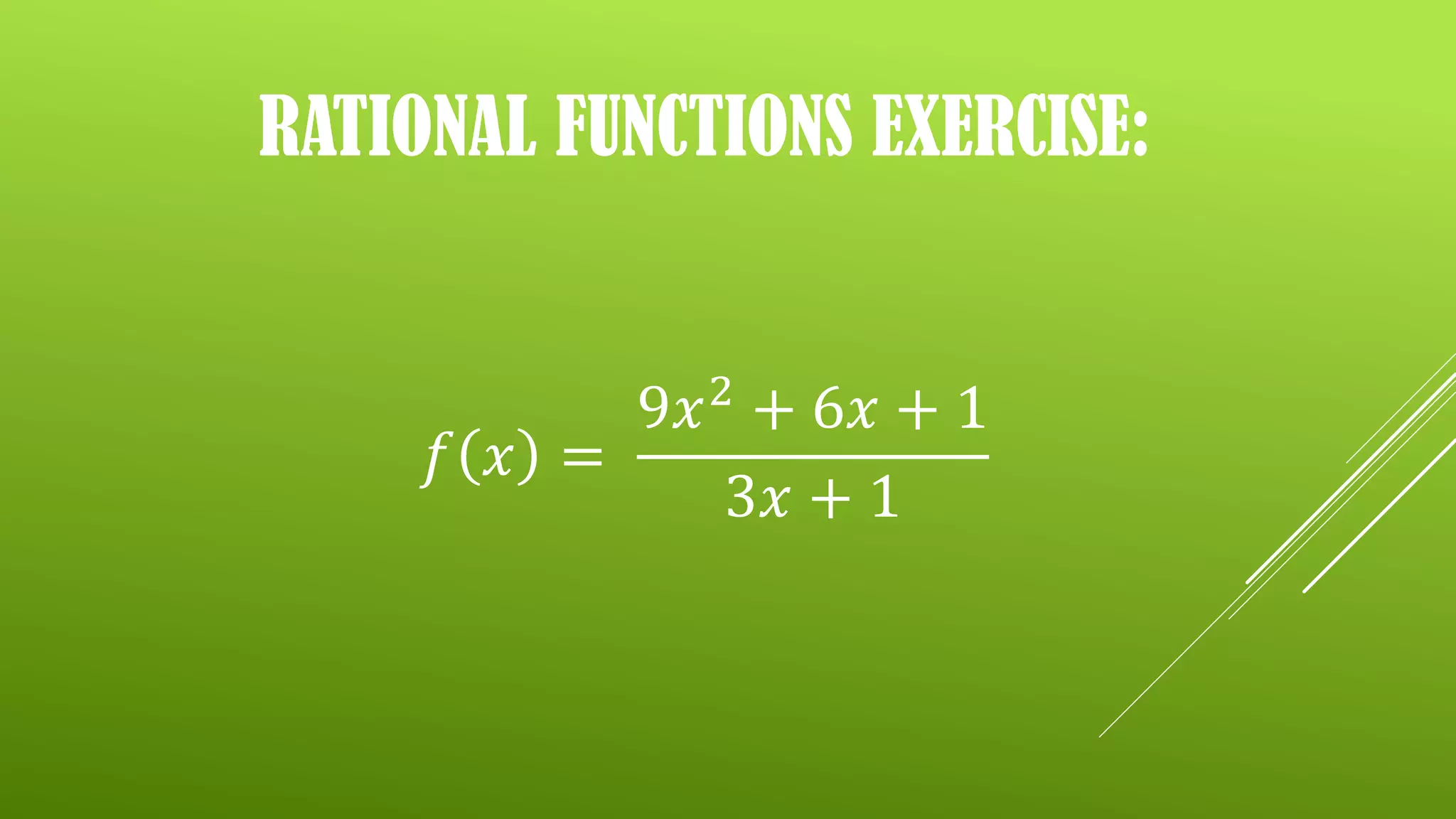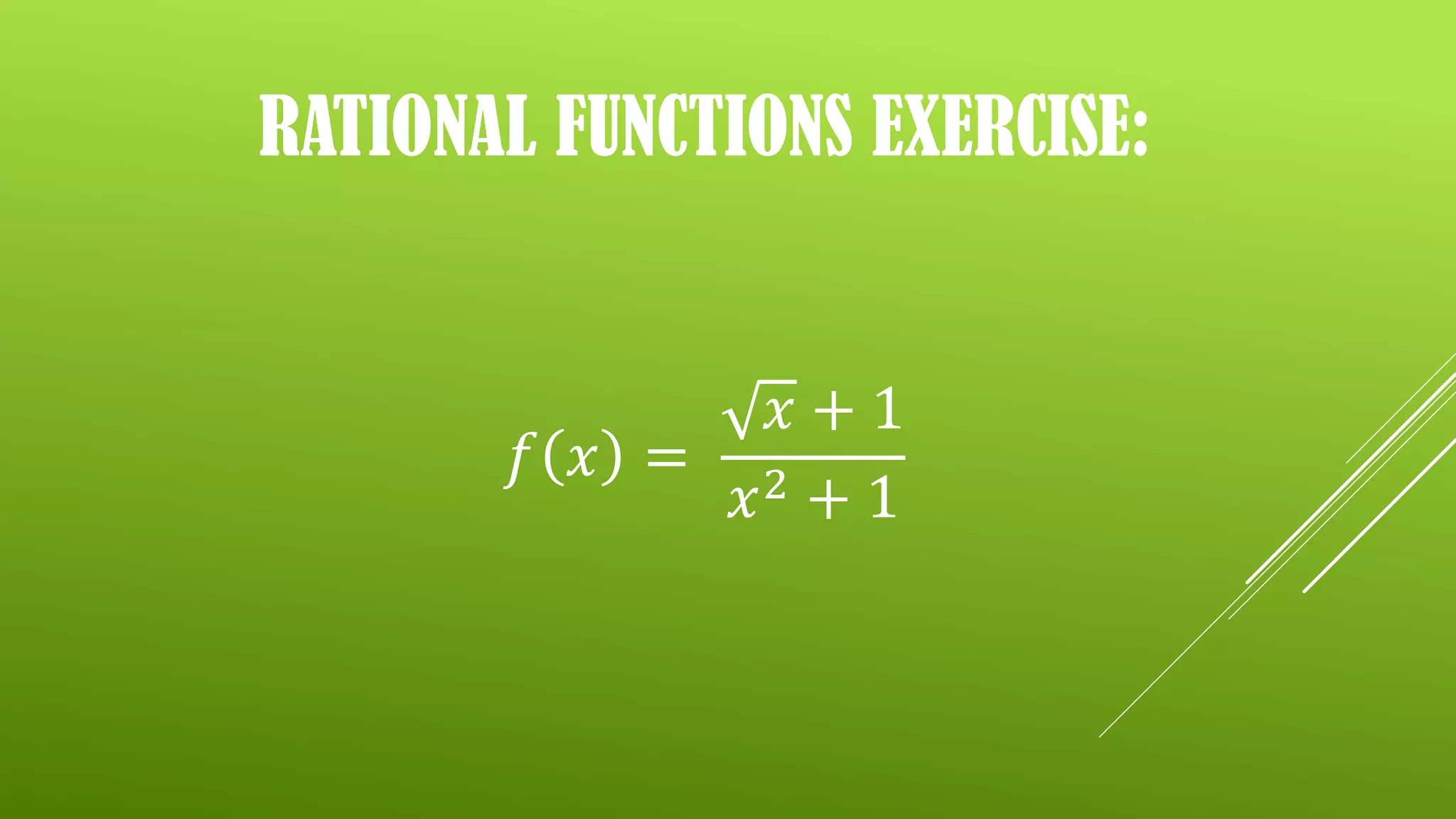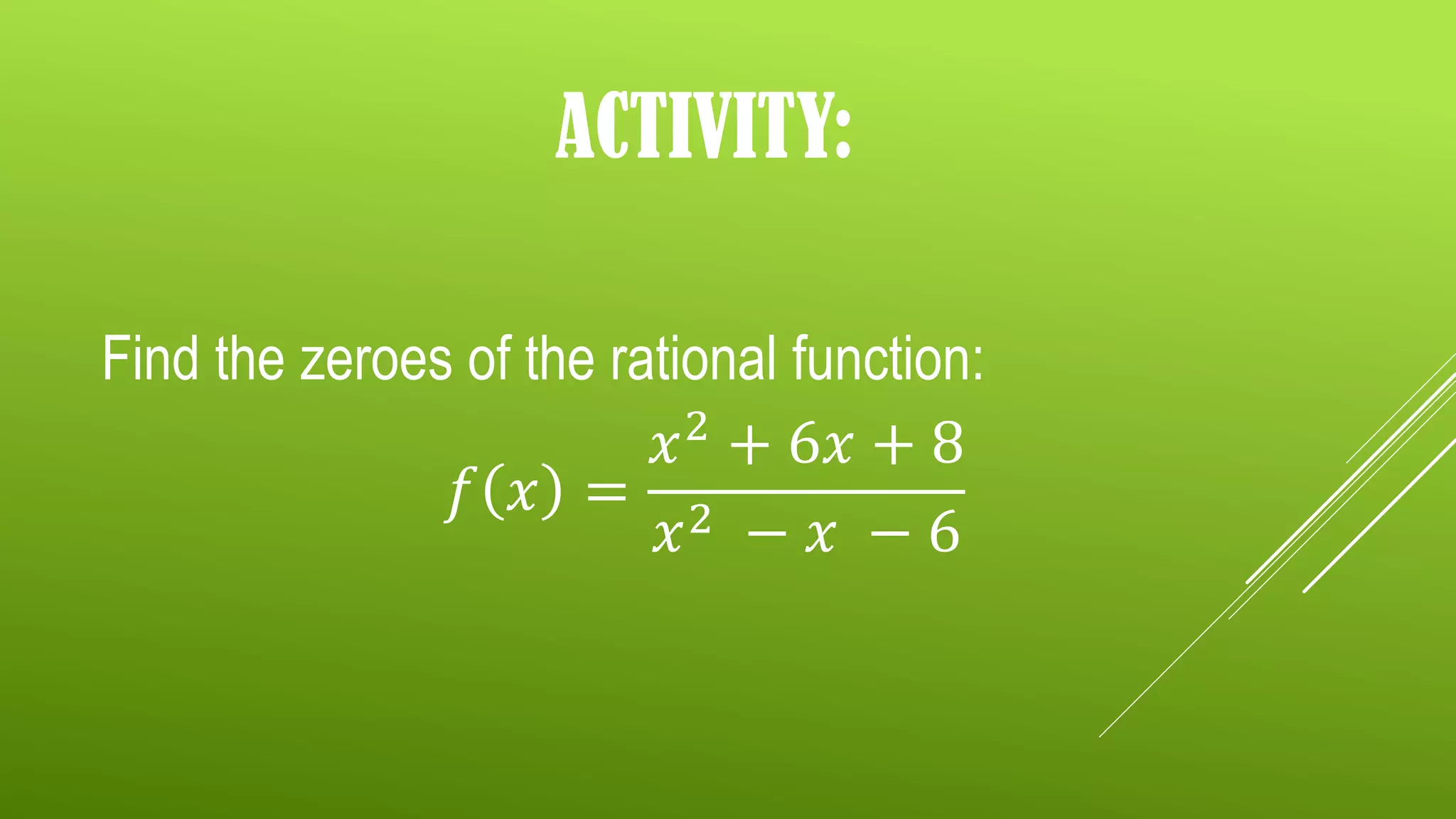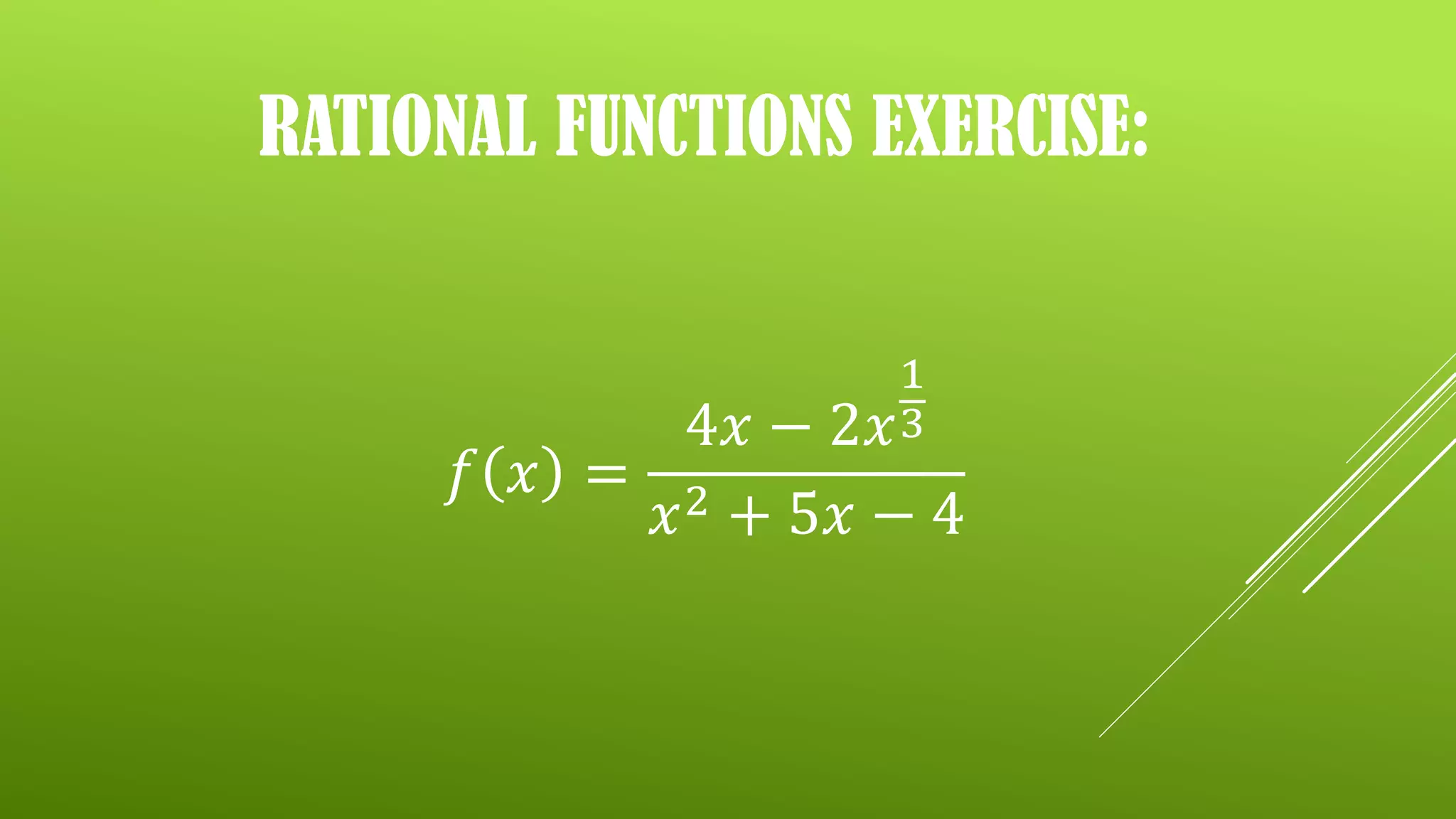
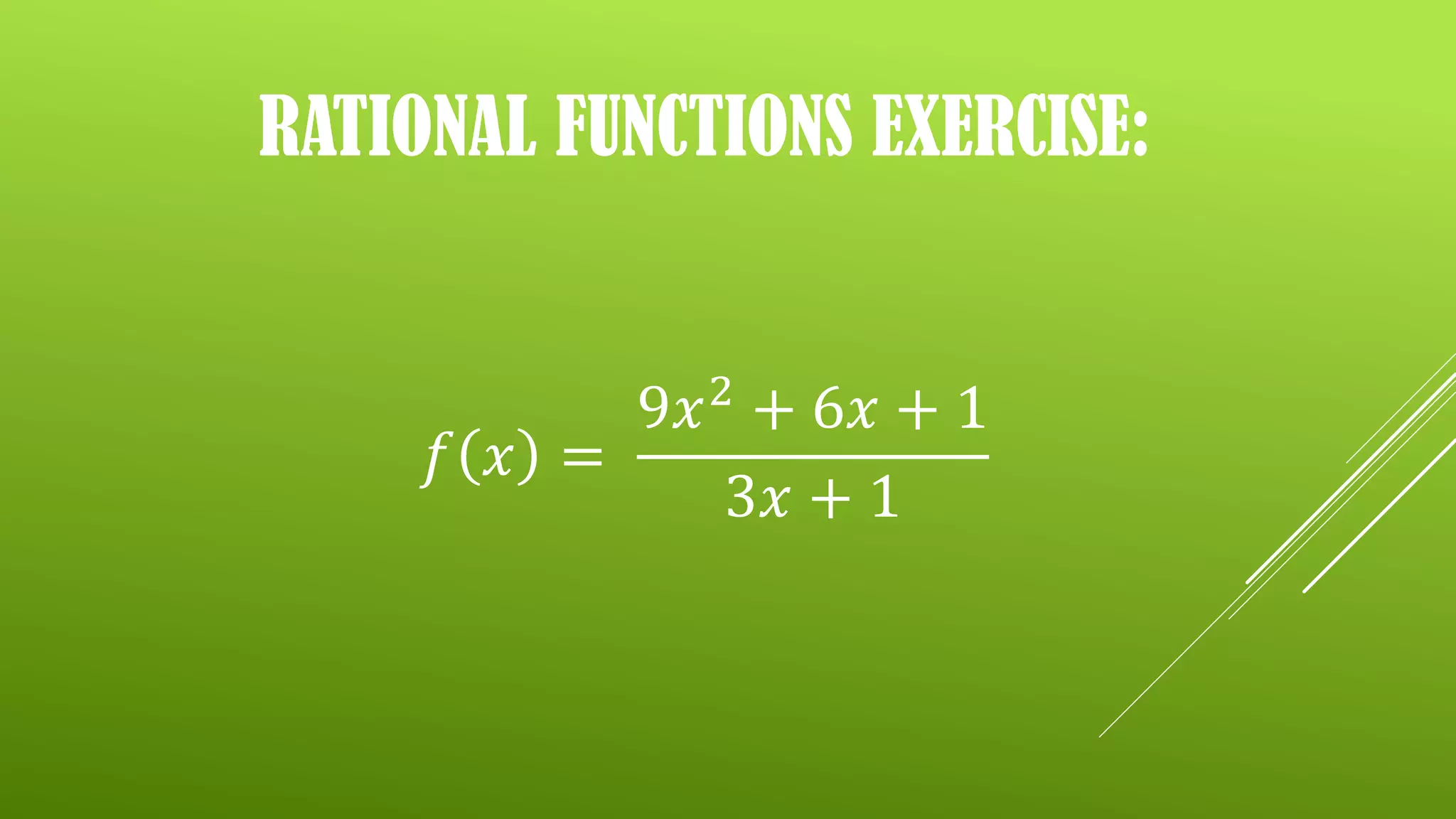
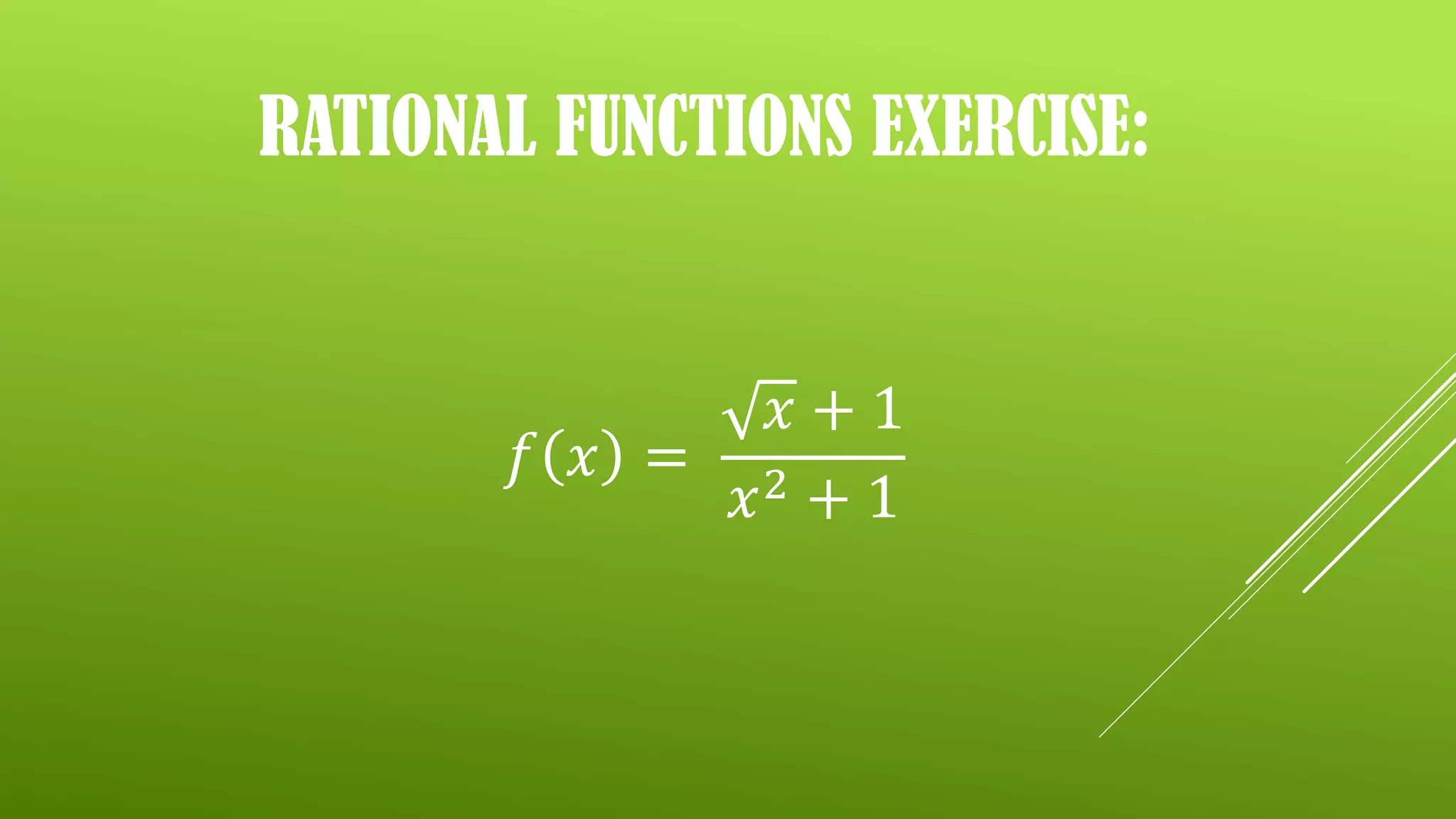
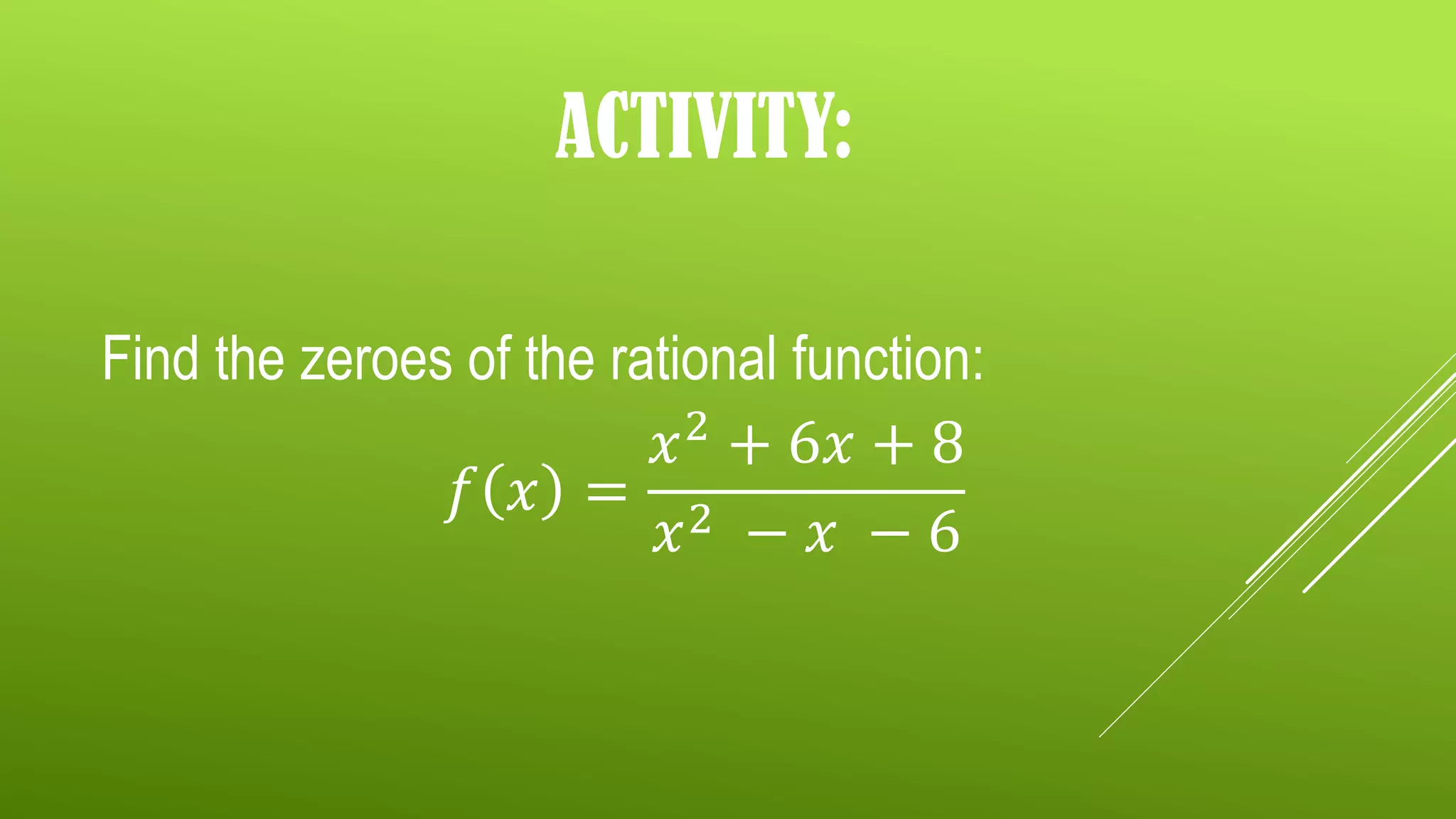
The document discusses rational functions, defined as functions that can be expressed as the ratio of two polynomials. It includes exercises on identifying rational functions, determining their domains and ranges, and finding their zeroes through specific steps. The document also provides assignments related to finding zeroes of various rational functions.

1. RATIONAL FUNCTIONS
General Mathematics

2. RATIONAL FUNCTIONS
It is a function that can be written in the form of:
𝑓 𝑥 =
𝑁(𝑥)
𝐷(𝑥)
Wherein N(x) and D(x) are both polynomials; D(x) must not
be a zero polynomial

3. RATIONAL FUNCTIONS EXERCISE:
Determine whether the functions presented are
considered rational or not:

4. RATIONAL FUNCTIONS EXERCISE:
𝑓 𝑥 =
4𝑥 − 2𝑥
1
3
𝑥2 + 5𝑥 − 4

5. RATIONAL FUNCTIONS EXERCISE:
𝑓 𝑥 =
9𝑥2
+ 6𝑥 + 1
3𝑥 + 1

6. RATIONAL FUNCTIONS EXERCISE:
𝑓 𝑥 =
𝑥 + 1
𝑥2 + 1

7. RATIONAL FUNCTIONS
Domain: All real numbers except any x-values that make the
denominator equals to 0
Range: Inverse Functions, Asymptotes

8. ZEROES OF RATIONAL FUNCTIONS
Steps in Finding Zeroes of Rational Functions:
1. Factor the numerator and denominator of the rational
function completely (if possible)
2. Identify the restrictions of the rational function (values that
will make the denominator equal to zero)
3. Identify the values that makes the numerator equal to zero
NOTE: these values must not be a restriction

9. ACTIVITY:
Find the zeroes of the rational function:
𝑓 𝑥 =
𝑥2
+ 6𝑥 + 8
𝑥2 − 𝑥 − 6

11. ASSIGNMENT:
(ZEROES OF RATIONAL FUNCTIONS)
1. 𝑓 𝑥 =
𝑥2−𝑥−12
𝑥2 −9
2. 𝑓 𝑥 =
𝑥+2
𝑥2 −3𝑥+2
3. 𝑓 𝑥 =
𝑥2−5𝑥−4
𝑥2 −4𝑥−1
4. 𝑓 𝑥 =
𝑥−5
𝑥2 −25
5. 𝑓 𝑥 =
𝑥2−7𝑥+6
𝑥2 −6𝑥+5