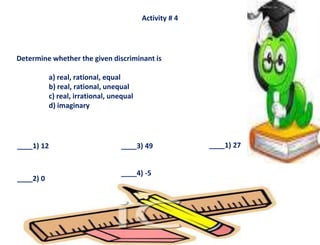
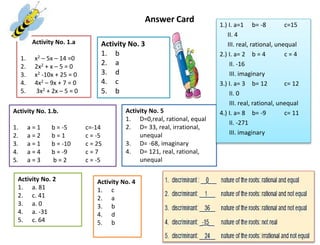
This document provides guidance on identifying the nature of roots of quadratic equations. It begins by identifying the least mastered skill of identifying the nature of roots. It then reviews the standard form of a quadratic equation and the quadratic formula. The key concept of the discriminant is explained, which determines the number and type of roots. Examples are provided to show how to find the discriminant and use it to describe the nature of roots. Activities are included for students to practice rewriting equations in standard form, finding a, b, c values, calculating discriminants, and determining the nature of roots. An assessment card with example problems is provided to check understanding.

1. Prepared by:
Maricel T. Mas
Lipay High School
Strategic Intervention Material
in Mathematics-IX
The Nature of the Roots
and The Discriminant

2. Guide Card
Least Mastered Skill:
• Identify the Nature of the Roots
Sub tasks:
 Identify values of a, b and c of a quadratic
equation,
 Find the discriminant; and
 Describe the nature of roots of quadratic
equation.

3. The Standard Form of
Quadratic Equation is…
ax2 + bx + c = 0
The Quadratic Formula is…
2
4
2
b b ac
x
a
  


4. WHY USE THE
QUADRATIC FORMULA?
 The quadratic formula allows you to solve ANY quadratic
equation, even if you cannot factor it.
 An important piece of the quadratic formula is what’s
under the radical:
b2 – 4ac
 This piece is called the discriminant.

5. WHY IS THE DISCRIMINANT
IMPORTANT?
The discriminant tells you the number and types of answers
(roots) you will get. The discriminant can be +, –, or 0
which actually tells you a lot! Since the discriminant is
under a radical, think about what it means if you have
a positive or negative number or 0 under the radical.
???

6. How to find the discriminant?
Example 1: Find the discriminant of
x
2
– 2x – 15 = 0
Step 2: Identify the value of a, b and c
a = 1 b = -2 c = -15
Step 3: Substitute these values to b
2
– 4ac
Step 1: Write first the
equation into
standard form
Solution:
D = b
2
– 4ac
D = (-2)
2
– 4(1)(15)
D = 64

7. Activity No. 1.a : Set Me To Your Standard
Now it’s your turn
Directions: Rewrite each quadratic equation in standard form.
1 x
2
– 5x = 14
2. 2x
2
+ x = 5
3. x
2
+ 25 = 10x
4. 4x
2
= 9x - 7
5. 3x
2
+ 2x = 5

8. Activity No. 1.b
Now it’s your turn
Directions: Using the given quadratic equations on activity no
1.b, identify the values of a, b, and c.
1. x
2
– 5x – 14 = 0
2. 2x
2
+ x = 5
3. x
2
+ 25 = 10x
4. 4x
2
– 9x + 7 = 0
5. 3x
2
+ 2x - 5 = 0
a = ___ b = ___ c = ___
a = ___ b = ___ c = ___
a = ___ b = ___ c = ___
a = ___ b = ___ c = ___
a = ___ b = ___ c = ___

9. Activity No. 2
Directions: Using the values of a, b, and c of Activity No. 1, find the discriminant
of the following using b
2
– 4ac:
1. x
2
– 5x – 14 = 0
2. 2x
2
+ x = 5
3. x
2
+ 25 = 10x
4. 4x
2
– 9x + 7 = 0
5. 3x
2
+ 2x - 5 = 0
a. 81 b. 11 c. -31
a. 39 b. - 39 c. 41
a. 0 b. 1 c. 100
a. - 31 b. 31 c. 81
a. -56 b. -64 c. 64

10. Let’s evaluate the
following equations.
1. x2
– 5x – 14 = 0
What number is under the radical
when simplified?
D=81
b2
– 4ac > 0, perfect square
 The nature of the roots :
REAL, RATIONAL, UNEQUAL
2. ) 2x2
+ x – 5 = 0
What number is under the
radical when simplified?
D= 41
b2
– 4ac > 0, not a perfect
square
The nature of the roots:
REAL, IRRATIONAL, UNEQUAL
4.) 4x2
– 9x + 7 = 0
What number is under the
radical when simplified?
D = –31
b2
– 4ac < 0, (negative)
The nature of the roots:
imaginary
3.) x2
– 10x + 25 = 0
What number is under the
radical when simplified?
D = 0
b2
– 4ac = 0
The nature of the roots:
REAL, RATIONAL, EQUAL

11. Determine whether the given discriminant is
a)greater than zero, perfect square
b) Greater than zero, not a perfect
square
c) Equals zero
d) Less than zero
____1) 95
____2) 225
____3) -9
____4) 0
____5) 63
Activity No. 3

12. Activity # 4
Determine whether the given discriminant is
a) real, rational, equal
b) real, rational, unequal
c) real, irrational, unequal
d) imaginary
____1) 12
____2) 0
____3) 49
____4) -5
____1) 27

13. Activity No. 5: Try These.
For each of the following quadratic equations,
a) Find the value of the discriminant, and
b) Describe the number and type of roots.
____1) x
2
+ 14x + 49 = 0
____2) . x
2
+ 5x – 2 = 0
____3) 3x
2
+ 8x + 11 = 0
____4) x
2
+ 5x – 24 = 0
D=____, ____________________
D=____, ____________________D=____, ____________________
D=____, ____________________

14. Assessment Card No. 1:
Write the values of a, b & c in the quadratic equation, then check the
discriminant and nature of roots of quadratic equation .
1. x2 – 8x + 15 = 0
I. a = ___ b = ___ c = ___
II. __ 4 __) 0 __ ) -4
__real, rational, equal
__real, rational, unequal
__real, irrational, unequal
__imaginary
2. 2x2 + 4x + 4 = 0
I. a = ___ b = ___ c = ___
II. __) 16 __) 0 __ ) -16
__real, rational, equal
__real, rational, unequal
__real, irrational, unequal
__imaginary

15. 3. 3x2 + 12x + 12 = 0
I. a = ___ b = ___ c = ___
II. __) 4 __) 0 __ ) -4
__real, rational, equal
__real, rational, unequal
__real, irrational, unequal
__imaginary
4. 8x2 - 9x + 11 = 0
I. a = ___ b = ___ c = ___
II. __) -172 __) -721 __ ) -271
__real, rational, equal
__real, rational, unequal
__real, irrational, unequal
__imaginary

16. Enrichment:
Directions: Determine the nature of the roots of the following
quadratic equations.

17. Answer Card
Activity No. 1.a
1. x2 – 5x – 14 =0
2. 2x2 + x – 5 = 0
3. x2 -10x + 25 = 0
4. 4x2 – 9x + 7 = 0
5. 3x2 + 2x – 5 = 0
Activity No. 1.b.
1. a = 1 b = -5 c=-14
2. a = 2 b = 1 c = -5
3. a = 1 b = -10 c = 25
4. a = 4 b = -9 c = 7
5. a = 3 b = 2 c = -5
Activity No. 2
1. a. 81
2. c. 41
3. a. 0
4. a. -31
5. c. 64
Activity No. 3
1. b
2. a
3. d
4. c
5. b
Activity No. 4
1. c
2. a
3. b
4. d
5. b
Activity No. 5
1. D=0,real, rational, equal
2. D= 33, real, irrational,
unequal
3. D= -68, imaginary
4. D= 121, real, rational,
unequal
1.) I. a=1 b= -8 c=15
II. 4
III. real, rational, unequal
2.) I. a= 2 b = 4 c = 4
II. -16
III. imaginary
3.) I. a= 3 b= 12 c= 12
II. 0
III. real, rational, unequal
4.) I. a= 8 b= -9 c= 11
II. -271
III. imaginary

18. References
Jose-Dilao, Soledad, Orines, and Bernabe,
Julieta G. Advanced Algebra, Trigonometry
and Statistics IV, SD Publications, Inc, 2009, p.
73
Learner’s Material Mathematics – Grade 9
First Edition, 2014 pp. 65-70.