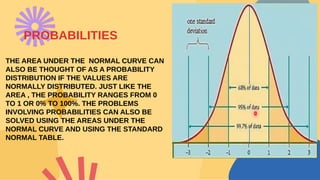
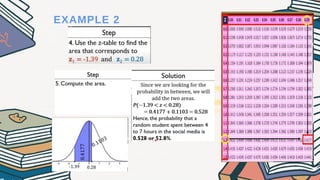
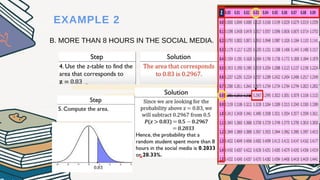
The document explains how to compute probabilities and percentiles using the standard normal table, detailing various cases such as finding probabilities greater than, less than, and between certain z-scores. It includes several examples related to normal distributions, such as household electricity consumption and social media usage among students. The content emphasizes that the area under the normal curve represents probability, ranging from 0 to 1.

1. Computes probabilities
and percentiles using
the standard normal
table.

2. SPECIFIC OBJECTIVES
SOLVE PROBLEMS INVOLVING
PROBABILITIES AND PER
ENTILES USING THE STANDARD
NORMAL CURVE.

3. PROBABILITY NOTATIONS
P(a  z  b)
P(z  a)
P(z  a)
Denotes the probability that the
z-score is between a and b.
Denotes the probability that the
z-score is greater than a.
Denotes the probability that the
z-score is less than a.

4. CASE 1
“greater than z”
“at least z”
“more than z”
“to the right of z”
“above z”
Example 1. Find the
probability of the
area above z = -1.
Example 2. Find the
probability of the
area above z = 1.

5. CASE 2
“less than z”
“at most z”
“no more than z”
“to the left of z”
Not greater than z
“below z”
Example 3. Find the
probability to the left
of z = -1.5.
Example 4. Find the
probability to the left
of z = 1.5.

6. CASE 3
“between and ”
“between and -”
Example 5. Find the
probability between
z = -2 and z = -1.5.
Example 6. Find the
probability between
z = 0.98 and z=
2.58.

7. CASE 4
“between and ”
“between and -”
Example 7. Find the
probability between
z = -1.32 and z =
2.37.
Example 8. Find the
probability between
z = 0.92 and
z= -1.75.

8. PROBABILITIES
THE AREA UNDER THE NORMAL CURVE CAN
ALSO BE THOUGHT OF AS A PROBABILITY
DISTRIBUTION IF THE VALUES ARE
NORMALLY DISTRIBUTED. JUST LIKE THE
AREA , THE PROBABILITY RANGES FROM 0
TO 1 OR 0% TO 100%. THE PROBLEMS
INVOLVING PROBABILITIES CAN ALSO BE
SOLVED USING THE AREAS UNDER THE
NORMAL CURVE AND USING THE STANDARD
NORMAL TABLE.

9. EXAMPLE 1
THE AVERAGE HOUSEHOLD
ELECTRICITY CONSUMPTION IN
THE COUNTRY IS 248 KWH. WHAT
IS THE PROBABILITY THAT A
HOUSEHOLD CONSUME LESS
THAN 180 KWH ASSUMING THAT
THE ELECTRICITY CONSUMPTION
IS NORMALLY DISTRIBUTED WITH
A STANDARD DEVIATION OF 56
KWH?

10. EXAMPLE 1
THE AVERAGE HOUSEHOLD
ELECTRICITY CONSUMPTION IN
THE COUNTRY IS 248 KWH. WHAT
IS THE PROBABILITY THAT A
HOUSEHOLD CONSUME LESS
THAN 180 KWH ASSUMING THAT
THE ELECTRICITY CONSUMPTION
IS NORMALLY DISTRIBUTED WITH
A STANDARD DEVIATION OF 56
KWH?

11. EXAMPLE 2

12. EXAMPLE 2
A. BETWEEN 4 TO 7 HOURS IN THE SOCIAL MEDIA.

13. EXAMPLE 2

14. EXAMPLE 2
B. MORE THAN 8 HOURS IN THE SOCIAL MEDIA.

15. EXAMPLE 2
B. MORE THAN 8 HOURS IN THE SOCIAL MEDIA.

16. Supposed that a school had 1,500
students, about how many students
spent more than 8 hours in the
social media?

17. A brisk walk at 4 miles per hour burns an average of 300
calories per hour. If the standard deviation of the
distribution is 8 calories. Find the probability that a
person who walks one hour at the rate of 4 miles per hour
will burn the following calories. Assume the variable to be
normally distributed.
a.More than 270 calories
b.Less than 295 calories
c.Between 278 and 318 calories
CHALLENGE TIME!

18. THANK YOU!