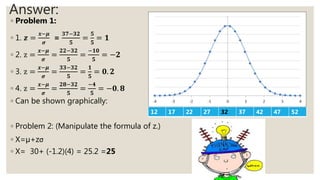
The document discusses converting normal random variables to standard normal variables and vice versa using z-scores. It provides examples of calculating z-scores given population/sample means and standard deviations. The key points are: - A z-score represents the distance from the mean in terms of standard deviations and is used to convert a raw score to its standard normal equivalent. - The formula for converting a normal variable to standard is z = (x - μ) / σ, where x is the raw score, μ is the population mean, and σ is the population standard deviation. - Converting from a z-score to a raw score uses the formula x = μ + zσ, allowing you to find the original value

1. Recapitulation:
◦ 1. What do you mean by
standard normal distribution?
The STANDARD NORMAL random
variable Z has a normal
distribution with mean = 0 and
standard deviation =1.
◦ 2. Using the standard table, what
is the area under the normal
curve below z=-2.8? above
z=1.29? between
◦ z=-0.28 and z=0.27?

2. Conversion Concept:
◦ 1. Convert 1 tablespoon to grams
◦ 2. Convert 20 degree Celsius to degree Fahrenheit.
◦ Note: use the formula: ℉ = ℃ ∙
9
5
+ 32
Ans: 1. 15 grams 2. 68 ℉

3. CONVERTING NORMAL RANDOM VARIABLE TO
STANDARD NORMAL VARIABLE & VICE VERSA
Prepared by:
Aileen D. Lositaňo
SHS Teacher
Daraga National High School

4. Activity (by partner)
Answer the following problems below.
◦ Follow the formula for z-score: 𝒛 =
𝒙−𝝁
𝝈
where x- raw
score, 𝜇-mean and 𝜎-standard deviation.
Note: two decimal places only for the final answer.
◦ Problem 1: The scores of STEM 1 students in the Final
examination for General Mathematics has a mean of 32
and a standard deviation of 5. Find the z-scores
corresponding to each of the following:
a. 37
b. 22
c. 33
◦ Problem 2: Find the raw score of a standard score of z =
-1.2 in a normally distributed population with mean 30
and standard deviation 4.
◦ Note: Use the formula for z. Slide 9

5. Answer:
◦ Problem 1:
◦ 1. 𝒛 =
𝒙−𝝁
𝝈
=
𝟑𝟕−𝟑𝟐
𝟓
=
𝟓
𝟓
= 𝟏
◦ 2. z =
𝒙−𝝁
𝝈
=
𝟐𝟐−𝟑𝟐
𝟓
=
−𝟏𝟎
𝟓
= −𝟐
◦ 3. z =
𝒙−𝝁
𝝈
=
𝟑𝟑−𝟑𝟐
𝟓
=
𝟏
𝟓
= 𝟎. 𝟐
◦ 4. z =
𝒙−𝝁
𝝈
=
𝟐𝟖−𝟑𝟐
𝟓
=
−𝟒
𝟓
= −𝟎. 𝟖
◦ Can be shown graphically:
◦ Problem 2: (Manipulate the formula of z.)
◦ X=µ+zσ
◦ X= 30+ (-1.2)(4) = 25.2 =25
12 17 22 27 32 37 42 47 52

6. Keep in mind!
◦ Any normal distribution can be transformed to standard normal distribution by
the formula:
𝑧 =
𝑥−𝜇
𝜎
where x-score, 𝜇-mean and 𝜎-standard deviation.
◦ Each of the values obtained using the given formula is called z-scores.
Note on notation: If we’re talking about an entire POPULATION that is normally
distributed, we use µ for the mean and σ for the standard deviation. If we’re talking
about a SAMPLE of a population that is normally distributed, we use 𝑋 for the mean
and s for standard deviation.
The standard score or z-score is a measure of relative standing. It represents the distance
between a given measurement X and the mean, expressed in standard deviations.
Z-score for population Z-score for sample
𝒛 =
𝒙−𝝁
𝝈 𝒛 =
𝒙 − 𝑿
𝒔

7. ◦ For any population, the mean and standard deviation are fixed. Thus, the z formula
matches the z-values one to one with the X values (raw scores). That is, for every X value
there corresponds a z-value and for each z-value there exactly one X value. The z-value
leads to the area under the curve found in the normal curve table, which is a
and that probability gives the desired percentage for X.
Example: In a given normal distribution, the sample mean is 20.5 and the sample standard
deviation is 5.4. Find the corresponding standard score of 18.
Solution: x=18 ; 𝑿 =20.5 ; s= 5.4
𝒛 =
𝒙− 𝑿
𝒔
=
𝟏𝟖−𝟐𝟎.𝟓
𝟓.𝟒
=
−𝟐.𝟓
𝟓.𝟒
= −𝟎. 𝟒𝟔 (The z-score that corresponds to a score of 18 is -0.46. It
tells us that the score of 18 is below average)
Example: The average score in a Statistics and Probability Test is 80 with standard deviation
10. What is the standard score of the following students? Carlos – 97 Shirly – 86
Carlos- 97 Shirly-86
𝒛 =
𝒙−𝝁
𝝈
=
𝟗𝟕−𝟖𝟎
𝟏𝟎
=
𝟏𝟕
𝟏𝟎
= 𝟏. 𝟕 𝒛 =
𝒙−𝝁
𝝈
=
𝟖𝟔−𝟖𝟎
𝟏𝟎
=
𝟔
𝟏𝟎
= 𝟎. 𝟔

8. *How many percent of students got below 81?
𝒛 =
𝒙−𝝁
𝝈
=
𝟖𝟏−𝟖𝟎
𝟏𝟎
=
𝟏
𝟏𝟎
= 𝟎. 𝟏
Using the z-table, look for the area below 0.1=0.5398 or
53.98%
There are 53.98% of students got below 81.
If the standard score z is given, the original or raw score x
can be obtained by solving
𝑧 =
𝑥 − 𝜇
𝜎
for x, yielding the equation, X=µ+zσ
For sample distribution, X= 𝑿+zs
Example on the 1st Activity

9. Convert from standard scores to normal random
variable
◦ Example: A highly selective university only admits the top 5% of the total examinees in their
entrance exam. The results of this year’s entrance exam follow a normal distribution with the mean
of 285 and a standard deviation of 12. What is the least score of an examinee who can be
admitted to the university?
Solution:
Look at the z-table and find a value of 0.95, this means that 0.05 or 5% are above this.
From the table, the value that is nearest to 0.95 is 0.9505 corresponds to 1.65 (intersection of 1.6
and .05). The z-score 1.65 has an area of 0.9505.
X= 285 + (1.65)(12)
X=304.8 =305

10. Boardwork:
Problem 1: The scores of Grade 11-ABM 2 students in
standardized test are normally distributed with the mean
of 60 and standard deviation of 8. Answer the following:
1. How many percent of the students got below 72?
2. What part of the group scored between 58 and 76?
3. If there were 250 students who took the test, about
how many students scored higher than 64?
Problem 2: Find the raw score of a standard score of z =
2.52 in a normally distributed population with mean 42
and standard deviation 3.

11. Answer:
◦ 1. 𝒛 =
𝒙−𝝁
𝝈
=
𝟕𝟐−𝟔𝟎
𝟖
=
𝟏𝟐
𝟖
= 𝟏. 𝟓 % below z-score 1.5= 0.9332 or 93.32%
◦ 2. 𝒛 =
𝒙−𝝁
𝝈
=
𝟓𝟖−𝟔𝟎
𝟖
=
−𝟐
𝟖
= −𝟎. 𝟐𝟓 %between z-scores -0.25 & 2 = 97.72%-
40.13%= 57.59%
◦ 𝒛 =
𝒙−𝝁
𝝈
=
𝟕𝟔−𝟔𝟎
𝟖
=
𝟏𝟔
𝟖
= 𝟐
◦ 3. 𝒛 =
𝒙−𝝁
𝝈
=
𝟔𝟒−𝟔𝟎
𝟖
=
𝟒
𝟖
= 𝟎. 𝟓 above 0.5=30.85%
250 x 30.85% =77.125 = 77
◦ There were 77 students out of 250 got a score higher than 64.
1. X=µ+zσ
X= 42+ (2.52)(3)= 49.56

12. Seatwork:
Given the following problem below.
1. Scores in the Precalculus Quarter Exam has mean 76 and standard
deviation 4, while the Gen. Math exam has mean 75 and standard deviation
5.
◦ If Catriona scored 90 in Precalculus and 91 in Gen. Math, in which subject
is her standing better? Assume that the scores in both exams are normally
distributed.
2. The weight of adults in Barangay Sagpon approaches a normal
distribution with a mean of 52.9 kg. and standard deviation of 7.2kg. If an
adult is chosen at random from Brgy. Sagpon, what is the probability that
his weight is above 48.5kg.
Additional Problem

13. Answer:
◦ 1. Solution:
◦ Answer: Catriona has a better standing in Precalculus than in Gen. Math.
◦ 2.
◦ 𝒛 =
𝒙−𝝁
𝝈
=
𝟒𝟖.𝟓−𝟓𝟐.𝟗
𝟕.𝟐
=
−𝟒.𝟒
𝟕.𝟐
= −𝟎. 𝟔𝟏
◦ Find the probability above -0.61 using the z-table: 72.91%
Precalculus - 90 General Math - 91
𝒛 =
𝒙−𝝁
𝝈
=
𝟗𝟎−𝟕𝟔
𝟒
=
𝟏𝟒
𝟒
= 𝟑. 𝟓 𝒛 =
𝟗𝟏−𝟕𝟓
𝟓
=
𝟏𝟔
𝟓
= 𝟑. 𝟐

14. Questions:
◦ What do you think is the importance of
converting raw scores to standard scores
(z-scores)?
◦ How can we apply the concept of
converting normal to standard normal
distribution?

15. Let’s sum
up your
learnings!

16. ◦ Questions:
◦ What is a standard score/z-score?
◦ How do we convert normal to standard
normal variable or vice versa?
◦ Why is it important to know the concept of
z-scores/standard normal distribution? How
do we apply it?

17. Quiz: (1/2 Crosswise)
1. A sample of bags of potato chips in a factory has
an average net weight of 24.7 grams with standard
deviation of 0.35 grams. What is the standard score
for two samples A and B with the following
weights?
A – 22.6 grams B – 25.9 gram
2. The weight of 2000 students are normally
distributed with the mean of 46kg and standard
deviation of 2.5kg?
a. How many students are less than 45kg?
b. bHow many students are heavier than
51.5kg?
c. If a student from this group is randomly
selected, what is the probability that he/she weight
between 45kg and 49kg?

18. Assignment:
1. The pulse rates of adult men approach a normal distribution with a mean of 80 bpm (beat per
minute) with standard deviation of 7bpm.
a. What percent of the adults have pulse rate of less than 70bpm?
b. What percent of adults have pulse rate of less than 70bpm?
c. If 60pbm to 100bpmis known to be normal, how many percent of the adults have above or
below normal pulse rates?

19. ◦ Thank You and God bless!!

20. Additional Problem:
◦ Problem: The IQs of 600 student applicants in a university are normally distributed with a mean
of 115 and standard deviation of 12. If only the top 10% applicants in terms of IQ will be
admitted, what is the least IQ a student must have in order to be admitted to the university?
◦ (Go back to slide 12)