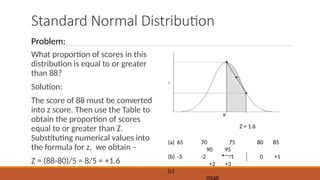
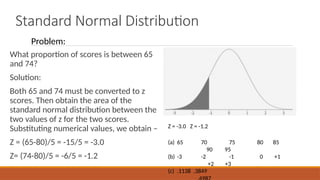
The document discusses the concept of normal distribution, characterized by its bell-shaped curve that is symmetric around the mean, with key properties including the empirical rule, which states that approximately 68%, 95%, and 99% of data falls within 1, 2, and 3 standard deviations from the mean, respectively. It also covers standard normal distribution with a mean of zero and a standard deviation of one, describing how to convert raw scores to z-scores and interpret them. Further topics include skewed distributions and kurtosis, which measures the tailedness of distributions, distinguishing between mesokurtic, platykurtic, and leptokurtic distributions.