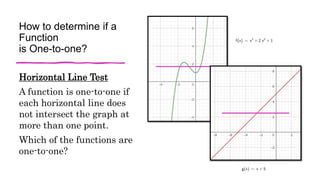
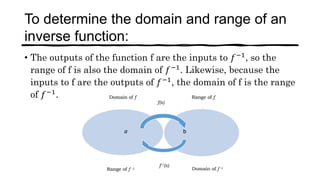
This document discusses one-to-one functions and their inverses. It defines a one-to-one function as a function where no two x-values are mapped to the same y-value. The inverse of a one-to-one function f is defined as f^-1 where the inputs and outputs are swapped. Examples are provided of finding the inverse of various functions by swapping variables and solving for y in terms of x. The domain of an inverse function is the range of the original function, and the range of the inverse is the domain of the original function.

1. One-to-one
Functions
General Mathematics - Week 4

2. Definition
The function f is one-to-one if
for any 𝒙𝟏, 𝒙𝟐 in the domain of
f, then 𝒇 𝒙𝟏 ≠ 𝒇 𝒙𝟐 . That is,
the same y-value is never
paired with two different x-
values.

3. Determine whether the
given relation is a
function. If it is a
function, determine
whether it is one-to-one
or not.

4. Determine
whether the
given relation is
a function. If it
is a function,
determine
whether it is
one-to-one or
not.
 The relation pairing an
SSS member to his or her
SSS number.
Solution:
Each SSS member is assigned
to a unique SSS number. Thus,
the relation is a function.
Further, two different
members cannot be assigned
the same SSS number. Thus,
the function is one-to-one.

5. Determine
whether the
given relation is
a function. If it
is a function,
determine
whether it is
one-to-one or
not.
 The relation pairing a real
number to its square.
Solution:
Each real number has a
unique perfect square. Thus,
the relation is a function.
However, two different real
numbers such as 2 and -2 may
have the same square. Thus,
the function is not one-to-one.

6. Determine whether the given relation
is a function. If it is a function,
determine whether it is one-to-one or
not.
 The relation pairing an airport to
its airport code.
Each real number has a unique perfect
square. Thus, the relation is a function.
However, two different real numbers
such as 2 and -2 may have the same
square. Thus, the function is not one-
to-one.

7. Examples:
• LAO – Laoag International
Airport
• MNL – Ninoy Aquino
International Airport
• CEB – Mactan-Cebu International
Airport
• DVO – Francisco Bangoy
International Airport (Davao)
• JFK – John F. Kennedy
International Airport (New York
City)
• ICN – Incheon International
Airport

8. Determine
whether the
given relation is
a function. If it
is a function,
determine
whether it is
one-to-one or
not.
 The relation pairing an
airport to its airport code.
Solution:
Since each airport has a
unique airport code, then the
relation is a function. Also,
since no two airports share the
same airport code, then the
function is one-to-one.

9. Determine
whether the
given relation is
a function. If it
is a function,
determine
whether it is
one-to-one or
not.
 The relation pairing an
airport to its airport code.
Solution:
Since each airport has a
unique airport code, then the
relation is a function. Also,
since no two airports share the
same airport code, then the
function is one-to-one.

10. How to determine if a
Function
is One-to-one?
Horizontal Line Test
A function is one-to-one if
each horizontal line does
not intersect the graph at
more than one point.
Which of the functions are
one-to-one?

11. Inverse of
One-to-one
Functions
General Mathematics - Week 4

12. Definition
Let f be a one-to-one function
with domain A and range B. then
the inverse of f, denoted by 𝑓−1
,
is a function with domain B and
range A defined by 𝑓−1
𝑦 = 𝑥 if
and only if 𝑓 𝑥 = 𝑦 for any y in
B.

13. To find the inverse of a
one-to-one function:
a) Write the function in the form y =
f(x);
b) Interchange the x and y
variables;
c) Solve for y in terms of x.

14. Example 1
• Find the inverse of
𝒇 𝒙 = 𝟑𝒙 + 𝟏.
Solution:
The equation of the function is
𝒚 = 𝟑𝒙 + 𝟏.
Interchange the x and y
variables 𝒙 = 𝟑𝒚 + 𝟏.
Solve for y in terms of x:
𝑥 = 3𝑦 + 1
𝑥 − 1 = 3𝑦
𝑥 − 1
3
=
3𝑦
3
𝑦 =
𝑥 − 1
3
Therefore, the inverse
of 𝑓 𝑥 = 3𝑥 + 1 is 𝑓−1
𝑥 =
𝑥−1
3
.

15. Example 2
• Find the inverse of
𝒈 𝒙 = 𝒙𝟑
− 𝟐.
Solution:
The equation of the
function is 𝒚 = 𝒙𝟑
− 𝟐.
Interchange the x and y
variables 𝒙 = 𝒚𝟑
− 𝟐
Solve for y in terms of x:
𝑥 = 𝑦3
− 2
𝑥 + 2 = 𝑦3
𝑦 =
3
𝑥 + 2
Thus, the inverse
of 𝑔 𝑥 = 𝑥3
− 2 is
𝑔−1
𝑥 =
3
𝑥 + 2.

16. Example 3
• Find the inverse of the rational
function
𝒇 𝒙 =
𝟐𝒙 + 𝟏
𝟑𝒙 − 𝟒
Solution:
The equation of the function is:
𝒚 =
𝟐𝒙 + 𝟏
𝟑𝒙 − 𝟒
Interchange the x and y variables:
𝒙 =
𝟐𝒚 + 𝟏
𝟑𝒚 − 𝟒
Solve for y in terms of x:
𝑥 =
2𝑦 + 1
3𝑦 − 4
𝑥 3𝑦 − 4 = 2𝑦 + 1
3𝑥𝑦 − 4𝑥 = 2𝑦 + 1
3𝑥𝑦 − 2𝑦 = 4𝑥 + 1
𝑦 3𝑥 − 2 = 4𝑥 + 1
𝑦 =
4𝑥 + 1
3𝑥 − 2
Therefore, the inverse of 𝑓 𝑥 =
2𝑥+1
3𝑥−4
is
𝒇−𝟏
𝒙 =
𝟒𝒙+𝟏
𝟑𝒙−𝟐
.

17. Example 4
• Find the inverse of
𝑓 𝑥 = 𝑥2 + 4𝑥 − 2, if it exists.
Solution:
Recognize that f(x) is a quadratic equation with a graph in the
shape of parabola that opens upward. It is not a one-to-one
function as it fails the horizontal line test.

18. Example 4
• Find the inverse of
𝑓 𝑥 = 𝑥2 + 4𝑥 − 2, if it exists.
Solution (Optional):
The equation of the function is
𝑦 = 𝑥2
+ 4𝑥 − 2
Interchange the x and y variables
𝑥 = 𝑦2
+ 4𝑦 − 2
Solve for y in terms of x:
𝑥 = 𝑦2
+ 4𝑦 − 2
𝑦2
+ 4𝑦 = 𝑥 + 2
𝑦2 + 4𝑦 + 4 = 𝑥 + 2 + 4
𝑦 + 2 2
= 𝑥 + 6
𝑦 + 2 = ± 𝑥 + 6
𝑦 = −2 ± 𝑥 + 6
The equation 𝑦 = −2 ± 𝑥 + 6 does not
represent a function because there are
some x-values that correspond to two
different values. Therefore, the
function 𝑓 𝑥 = 𝑥2
+ 4𝑥 − 2 has no
inverse function.

19. Representations of
Inverse Functions
General Mathematics - Week 4

20. In using table of values of the functions, first we need to
ascertain that the given function is a one-to-one function
wherein no x-values are repeated. It is represented as the
x-values of the function resulted as the y-values of its
inverse, and the y-values of the function are the x-values
of its inverse. Also, the graph should correspond to a one-
to-one function by applying the Horizontal Line test. If it
passes the test, the corresponding function is one-to-one.
Given the graph of a one-to-one function, the graph of its
inverse can be obtained by reflecting the graph about the
line y = x.

25. Domain and
Range of Inverse
Functions
General Mathematics - Week 4

26. To determine the domain and range of an
inverse function:
• The outputs of the function f are the inputs to 𝑓−1, so the
range of f is also the domain of 𝑓−1. Likewise, because the
inputs to f are the outputs of 𝑓−1, the domain of f is the range
of 𝑓−1.

27. To determine the domain and range of an
inverse function:
• This means that the domain of the inverse is the range of the
original function and that the range of the inverse is the
domain of the original function.

28. Example 1
• Find the domain and range of
𝑓 𝑥 = 2𝑥 + 1 and its inverse.
Solution:
Let 𝑦 = 2𝑥 + 1
Interchange x and y:
𝑥 = 2𝑦 + 1
Solve for y:
2𝑦 = 𝑥 − 1
𝑦 =
𝑥 − 1
2
𝑓 𝑥 = 2𝑥 + 1
𝑓−1
𝑥 =
𝑥 − 1
2
The domain and range of the
function and its inverse are as
follows:
𝑓 𝑥 𝑓−1 𝑥
Domain 𝑥 𝜖 ℝ 𝑥 𝜖 ℝ
Range 𝑦 𝜖 ℝ 𝑦 𝜖 ℝ

29. Example 2
• Find the domain and
range of 𝑓 𝑥 =
5𝑥−1
−𝑥+2
.
Solution:
Let 𝑦 =
5𝑥−1
−𝑥+2
Interchange x and y:
𝑥 =
5𝑦 − 1
−𝑦 + 2
Solve for y:
𝑥 −𝑦 + 2 = 5𝑦 − 1
−𝑥𝑦 + 2𝑥 = 5𝑦 − 1
−𝑥𝑦 − 5𝑦 = −2𝑥 − 1
𝑥𝑦 + 5𝑦 = 2𝑥 + 1
𝑦 𝑥 + 5 = 2𝑥 + 1
𝑦 =
2𝑥 + 1
𝑥 + 5

30. Example 2 (cont.)
𝑓 𝑥 =
5𝑥 − 1
−𝑥 + 2
𝑓−1 𝑥 =
2𝑥 + 1
𝑥 + 5
The domain and range of the function and its inverse are as
follows:
𝑓 𝑥 𝑓−1 𝑥
Domain 𝑥 𝜖 ℝ ∕ 𝑥 ≠ 2 𝑥 𝜖 ℝ 𝑥 ≠ −5
Range 𝑦 𝜖 ℝ 𝑦 ≠ −5 𝑦 𝜖 ℝ ∕ 𝑦 ≠ 2