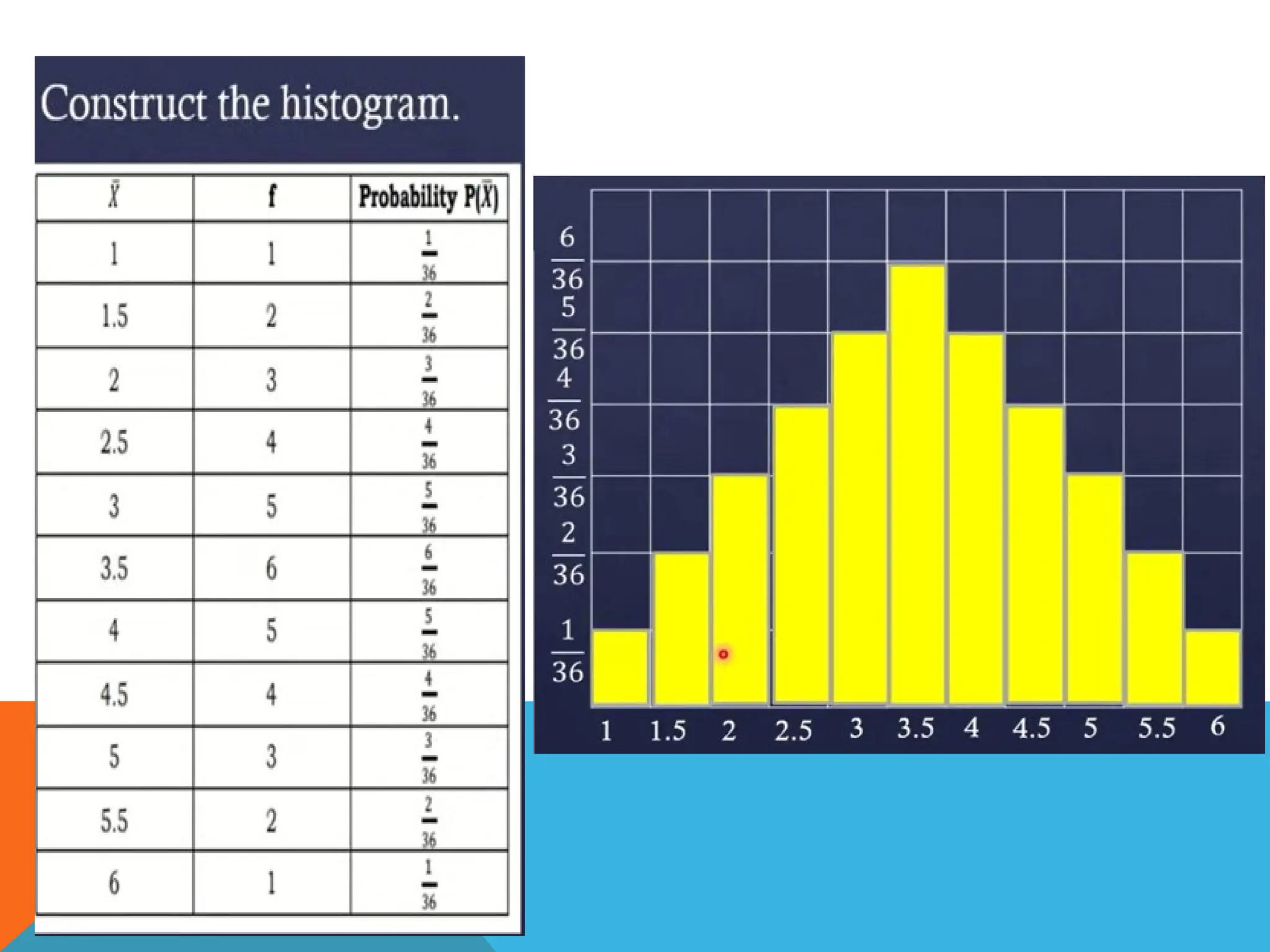
This document outlines the objectives for a lesson on the central limit theorem, focusing on concepts like sampling distributions and problem-solving with sample means. It provides examples using a die to illustrate how to compute population mean, variance, and standard deviation, as well as how to construct histograms for sampling distributions. The document aims to help students understand the approaches of the sampling distribution of the mean as sample sizes increase.

1. CEN
TRAL
LIM
IT
TH
EO
REM

2. SPECIFIC OBJECTIVES
At the end of the lesson, the students should be
able to:
1. Illustrates the Central Limit Theorem. M11/12SP-IIIe-
2
2. Defines the sampling distribution of the sample mean
using the Central Limit Theorem. M11/12SP-III-3
3. Solves problems involving sampling distributions of
the sample mean. M11SP-IIIe-f-1

3. CENTRAL LIMIT THEOREM
If random samples of size n are drawn
from a population, then as n becomes larger, the
sampling distribution of the mean approaches
the normal distribution, regardless of the shape
of the population distribution.

4. ILLUSTRATING CENTRAL LIMIT THEOREM
Given a die, it has 6 faces in which each face has
either dot/s of x= 1,2,3,4,5 and 6. Compute the
following:
1. Population mean
2. Population variance
3. Population standard deviation
4. Draw the probability histogram of the sampling
distribution of the means.

5. COMPUTE THE POPULATION MEAN
µ
COMPUTE THE POPULATION VARIANCE
= 2.92
𝝈𝟐
=𝜮 ¿¿

6. COMPUTE THE POPULATION STANDARD
DEVIATION
σ =
σ =
σ =
σ = 1.71

7. CONSTRUCT THE HISTOGRAM
PROBABILITY
SAMPLE MEAN

8. Given a die, it has 6 faces in which each face has
either dot/s of x= 1,2,3,4,5 and 6. Given it as
population, consider the samples of size n = 2.
Compute the following:
1.Mean of the sampling distribution of the sample
mean.
2.Variance of the sampling distribution of the sample
mean.
3.Standard deviation of the sampling distribution of
the sample mean.
4.Illustrate the probability histogram of the sample
distribution of the mean.

9. 1,1 3,1
1,2 3,2
1,3 3,3
1,4 3,4
1,5 3,5
1,6 3,6
2,1 4,1
2,2 4,2
2,3 4,3
2,4 4,4
2,5 4,5
2,6 4,6
5,1
5,2
5,3
5,4
5,5
5,6
6,1
6,2
6,3
6,4
6,5
6,6
X = 1,2,3,4,5 and 6, n=2
POSSIBLE SAMPLE

11. COMPUTE THE MEAN OF THE SAMPLING DISTRIBUTION OF THE SAMPLE MEAN
COMPUTE THE VARIANCE OF THE SAMPLING DISTRIBUTION OF THE SAMPLE MEAN.
COMPUTE THE STANDARD DEVIATION OF THE SAMPLING DISTRIBUTION OF THE
SAMPLE MEAN..

23. https://www.youtube.com/watch?v=Sq_XTpslmMI&list=PPSV
WOW MATH
REFERENCES: