This document contains a summary of key concepts in statistics: - Statistics involves collecting and analyzing data to make inferences about populations. It has two broad areas: descriptive statistics which organizes data, and inferential statistics which makes conclusions about populations based on samples. - Variables can be either qualitative (represent categories) or quantitative (represent numerical amounts). Examples of each are given. 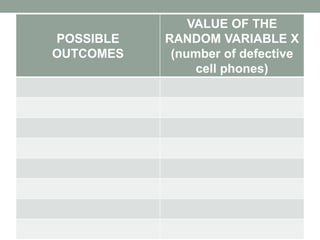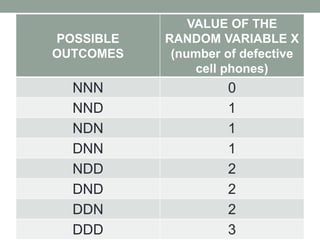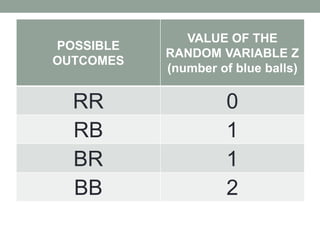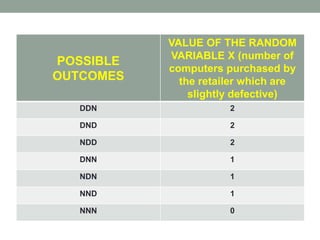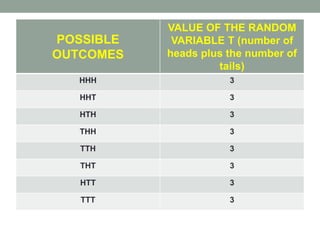- Random variables assign numerical values to outcomes of experiments. They can be either discrete (countable outcomes) or continuous (measured on a scale). Examples of each are provided.

1. Dear Lord,
May we through your guidance
Add love to the world,
Subtract evil from our lives
Multiply your good works to your children
And divide your gifts and share them to
others.
This we pray in the name of Mary, our
mother and Jesus Christ, our Lord. Amen.
MATHEMATICS PRAYER

3. Statistics
It is a collection of methods for
planning experiments, obtaining
data, and then analyzing,
interpreting and drawing
conclusions based on the data.

4. • It has two broad areas, namely,
descriptive statistics and inferential
statistics.
• Descriptive Statistics – deals primarily
with the collection and organization of data.
• Inferential Statistics -deals with making
inferences or conclusions about a
population based on the findings of the
study conducted on a sample.

5. Basic Terms in Statistics
• Data– are the values that variables can assume
• Variable – is a characteristics that is observable
or measurable in every unit of universe.
• Population – is the set of a all possible values of
a variable
• Sample - is a subgroup of a population.

6. 1. Qualitative Variables –
•words or codes that represent a class
or category
•express a categorical attribute
- gender
- religion
- marital status
- highest educational attainment
REVIEW:
Classification of Variables

7. 2. Quantitative Variables
•number that represent an amount or
count.
•numerical data, sizes are meaningful and
answer questions as “how may” or “how
much”
- height
- weight
- number of registered cars

8. Which of the variables are qualitative? Which are
quantitative?
• highest educational attainment
• body temperature
• civil status
• brand of laundry soap being used
• total household expenditures last month in pesos
• number of children in the household
• time (in hours) consumed on Facebook on a
particular day
qualitative
quantitative
qualitative
qualitative
quantitative
quantitative
quantitative

9. EXPLORING
RANDOM
VARIABLES
1st Week

10. Objectives
•At the end of the lesson the students
should be able to:
a) Illustrate a random variable;
b) Find the possible values of a random
variable.
c) Manifest active participation in the
teaching learning process.

11. Experiment

12. Experiment
•Any activity, which can
be done repeatedly
under similar
conditions.

13. Sample Space
•Set of all possible
outcomes of an
experiment.

14. GETTING READY
•If two coins are tossed, what numbers
can be assigned for the frequency of
heads that will occur?
•Note: The answer to this questions
require an understanding of random
variables.

15. Random Variable
Random Variable a
numerical quantity that
is assigned to the
outcome of an
experiment .

16. Illustrative Example
1. Supposed two coins are tossed. Let X be the
random variable representing the number of heads
that occur. Find the values of random variable X.
H
T
H
T
H
T
Sample Space = { HH, HT, TH, TT }
Possible
outcomes
Value of random
variable X(number
of heads)
HH 2
HT 1
TH 1
TT 0
The values of the random variable X (number of heads) in
this experiment are 0, 1 and 2.
X = { 0, 1 , 2 }

17. 2. Supposed three coins are tossed. Let Y be the
random variable representing the number of tails that
occur. Find the values of random variable Y.
H
T
H
T
H
T
Sample
Space =
{ HHH, HHT,
HTH, HTT,
THH, THT,
TTH, TTT}
The values of the random variable Y
(number of tails) in this experiment
are 0, 1, 2 and 3.
Y = { 0, 1 , 2, 3 }
H
T
H
T
H
T
H
T
Possible
outcomes
Value of
random
variable
Y(number of
tails)
HHH 0
HHT 1
HTH 1
HTT 2
THH 1
THT 2
TTH 2
TTT 3

18. GROUP ACTIVITY
DEFECTIVE CELL PHONES
• Suppose three cell phones are tested at random.
We want to find out the number of defective cell
phones that occur. Thus, to each outcomes in the
sample space we shall assign a value.
Let D represent the defective cell phone and
N represent the non-defective cell phone. If we
let X be the random variable representing the
number of defective cell phones, can you show the
values of random variable X?

19. POSSIBLE
OUTCOMES
VALUE OF THE
RANDOM VARIABLE X
(number of defective
cell phones)

20. POSSIBLE
OUTCOMES
VALUE OF THE
RANDOM VARIABLE X
(number of defective
cell phones)
NNN 0
NND 1
NDN 1
DNN 1
NDD 2
DND 2
DDN 2
DDD 3

21. So, the possible values of random
variable X are 0, 1, 2, and 3

22. ACTIVITY 3
• Two ball are drawn in succession without
replacement from an urn containing 5 red balls
and 6 blue balls. Let Z be the random variable
representing the number of blue balls. Find the
values of the random variable Z.
• Four coins are tossed. Let Z be the random
variable representing the number of heads that
occur. Find the values of the random variable Z.

23. ACTIVITY 3
•Two ball are drawn in succession
without replacement from an urn
containing 5 red balls and 6 blue
balls. Let Z be the random variable
representing the number of blue
balls. Find the values of the
random variable Z.

24. POSSIBLE
OUTCOMES
VALUE OF THE
RANDOM VARIABLE Z
(number of blue balls)

25. POSSIBLE
OUTCOMES
VALUE OF THE
RANDOM VARIABLE Z
(number of blue balls)
RR 0
RB 1
BR 1
BB 2

26. So, the possible values of random
variable Z are 0, 1, and 2

27. 1.Four coins are tossed. Let
Z be the random variable
representing the number
of heads that occur. Find
the values of the random
variable Z.

28. Probability and
Statistics

29. Experiment
Sample Space
Random Variable

30. Random Variable
•Is a function that associates
a real number to each
element in the sample
space. It is a variable whose
values are determined by
chance.

31. REVIEW

32. 1. A shipment of five computers contains
two that are slightly defective. If a retailer
receives three computers at random, list
the elements of the sample space S using
the letter D and N for defective and non-
defective computers, respectively. To each
sample point assign a value x the random
variable X representing the number of
computers purchased by the retailer
which are slightly defective.

33. POSSIBLE
OUTCOMES
VALUE OF THE RANDOM
VARIABLE X (number of
computers purchased by
the retailer which are
slightly defective)

34. POSSIBLE
OUTCOMES
VALUE OF THE RANDOM
VARIABLE X (number of
computers purchased by
the retailer which are
slightly defective)
DDN 2
DND 2
NDD 2
DNN 1
NDN 1
NND 1
NNN 0

35. 2. Let T be a random variable
giving the number of heads plus
the number of tails in three tosses
of coin. List the elements of the
sample space S for the three
tosses of the coin and assign a
value to each sample point.

36. POSSIBLE
OUTCOMES
VALUE OF THE RANDOM
VARIABLE T (number of
heads plus the number of
tails)

37. POSSIBLE
OUTCOMES
VALUE OF THE RANDOM
VARIABLE T (number of
heads plus the number of
tails)
HHH 3
HHT 3
HTH 3
THH 3
TTH 3
THT 3
HTT 3
TTT 3

38. The random variable in the
preceding activities are
countable…

39. DISCRETE RANDOM
VARIABLE
CONTINUOUS RANDOM
VARIABLE

40. DISCRETE RANDOM
VARIABLE
•It is a random variable where the
set of possible outcomes is
countable. Mostly, discrete random
variables represent count data,
such as the number of defective
chairs produced in a factory.

41. CONTINUOUS RANDOM
VARIABLE
•It is a random variable where it
takes on values on a continuous
scale. Often, continuous random
variables represent measured
data, such as heights, weights,
and temperatures.

42. Classify the following random
variables as discrete or continuous.
1. The number of defective computers produced
by a manufacturer.
2. The weight of the new-borns each year in a
hospital.
3. The number of siblings in a family of a region.
4. The amount of paint utilized in a building
project.
5. The number of dropout in a school district for a
period of 10 years.

43. 6. The speed of a car.
7. The number of female athletes.
8. The time needed to finish the test.
9. The amount of sugar in a cup of
coffee.
10.The number of people who are
playing LOTTO each day.

44. EXERCISES

45. Classify the following random variables as
discrete or continuous.
1. The number of accidents per year at an
intersection.
2. The number of voters favoring a candidate.
3. The number of bushels of apples per hectare
this year.
4. The average amount of electricity consumed
per household per month.
5. The number of deaths per year attributed to
lung cancer

46. Thank you
and
God bless as all…