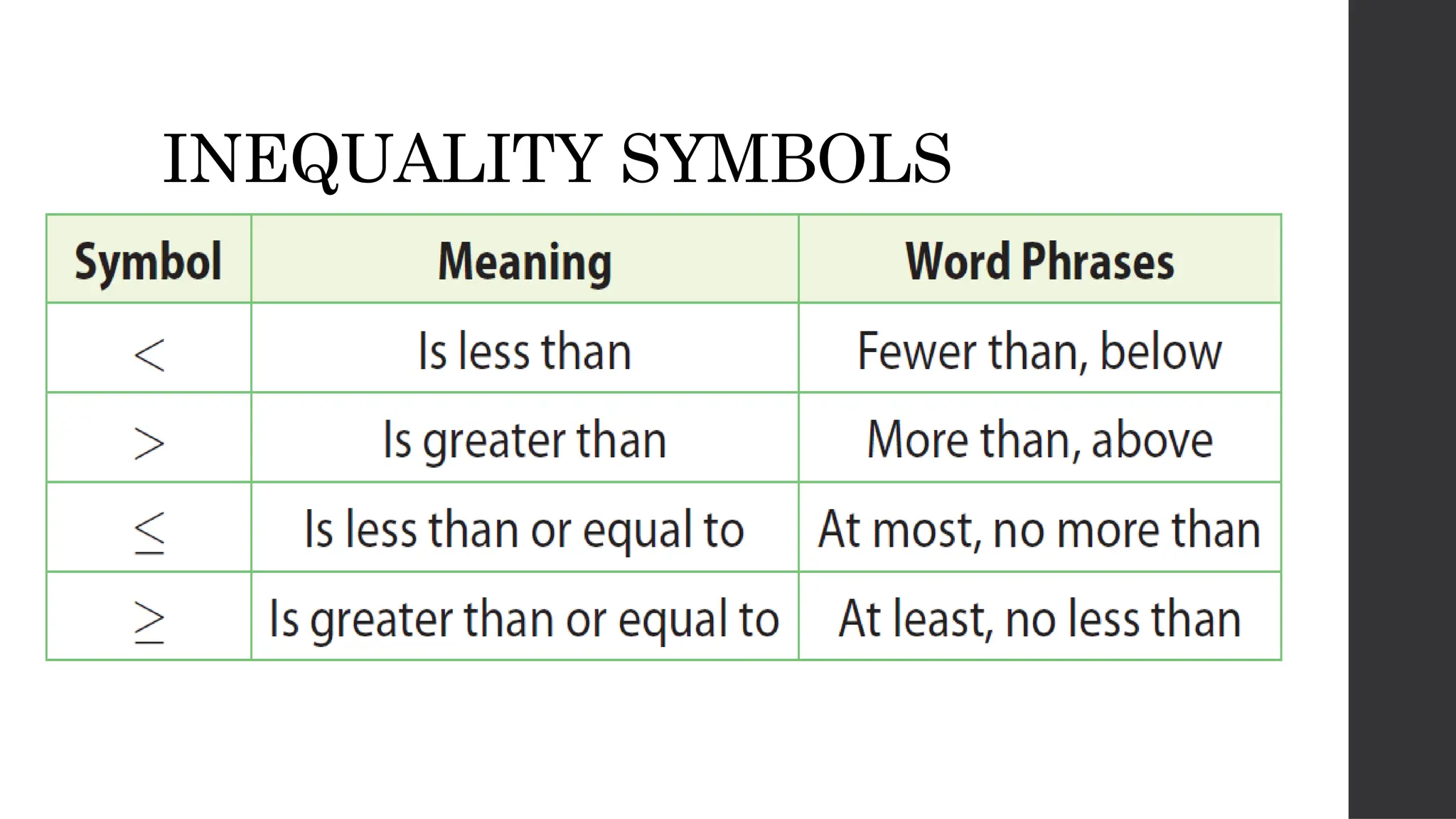
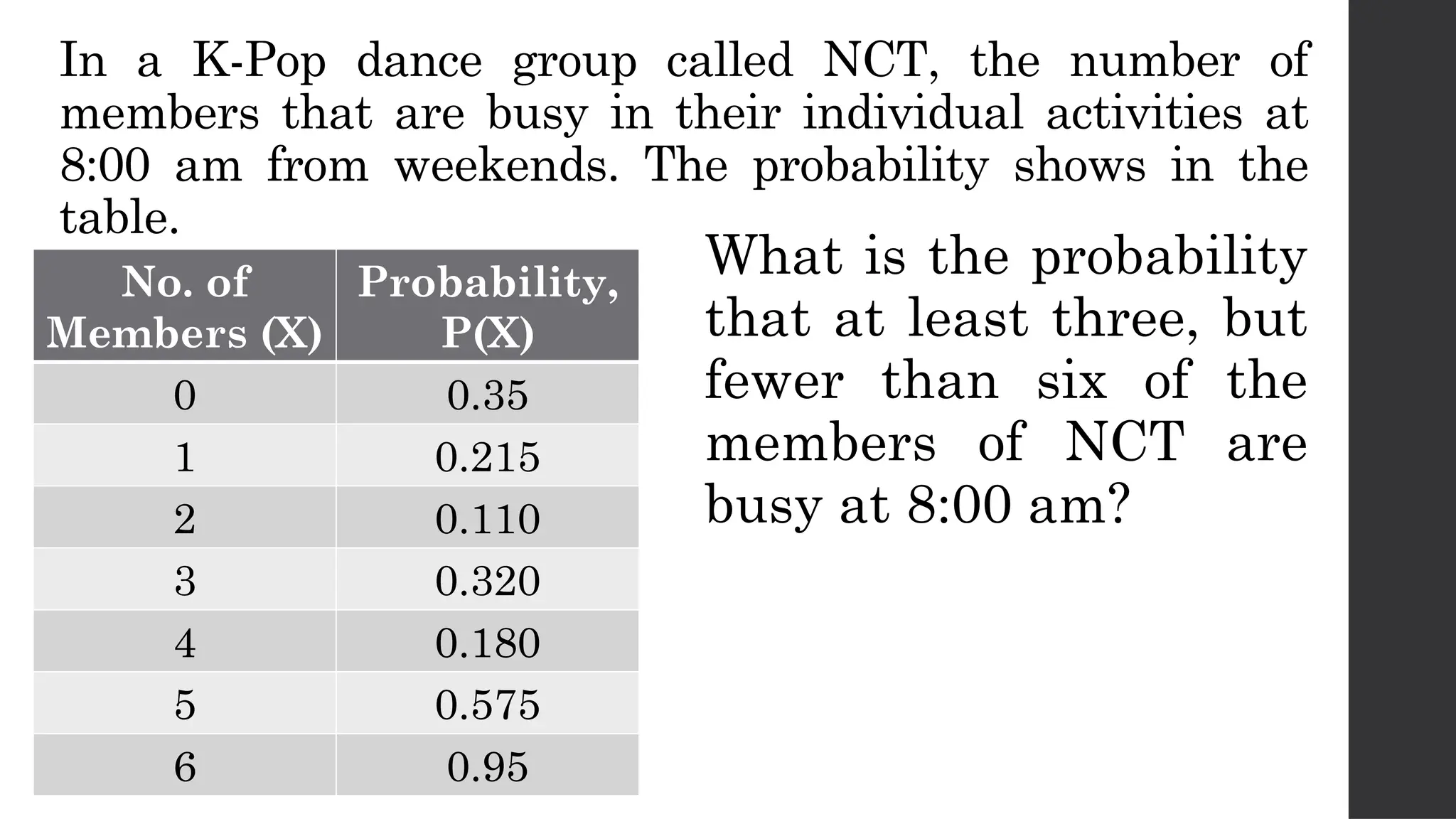
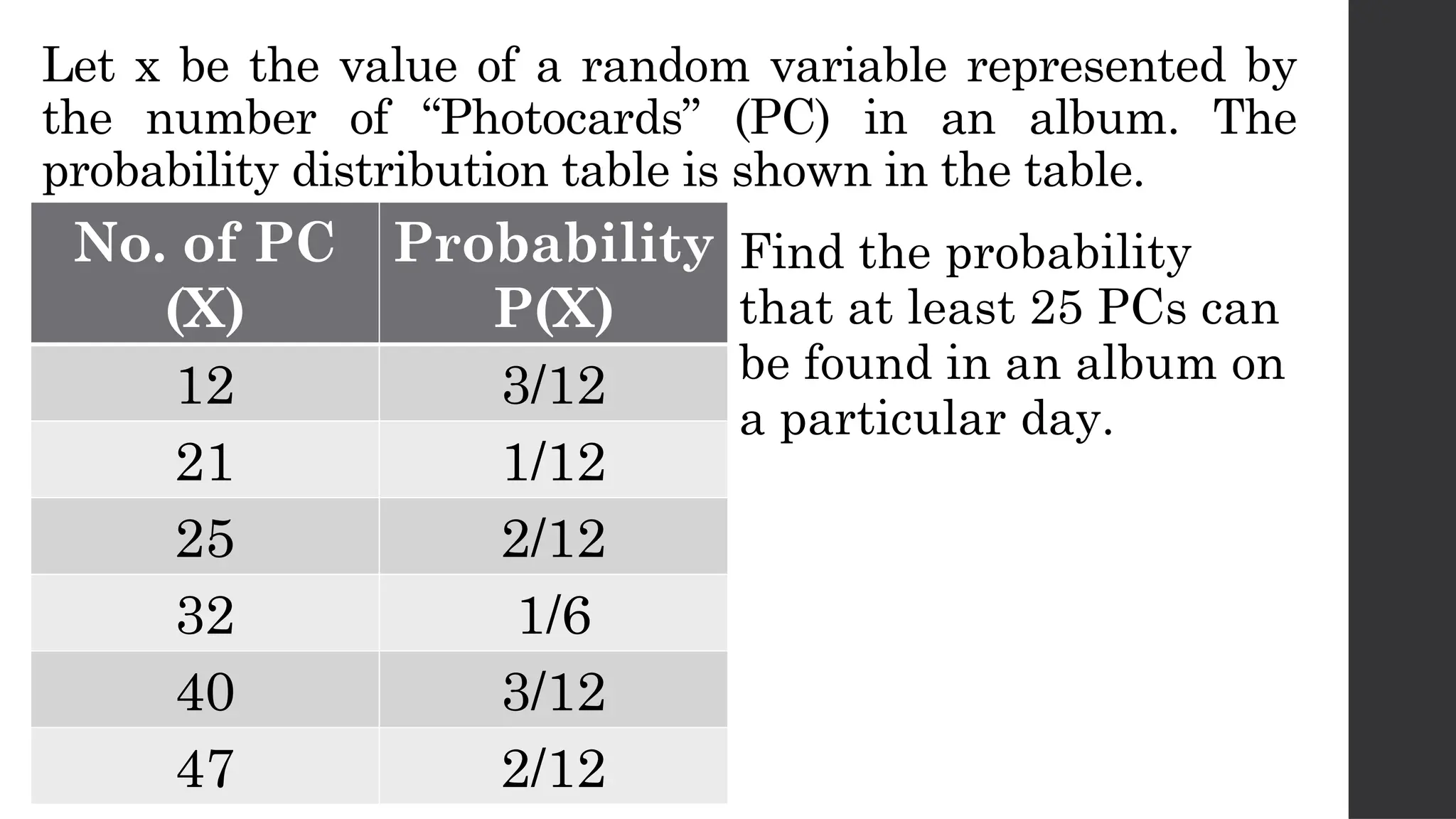
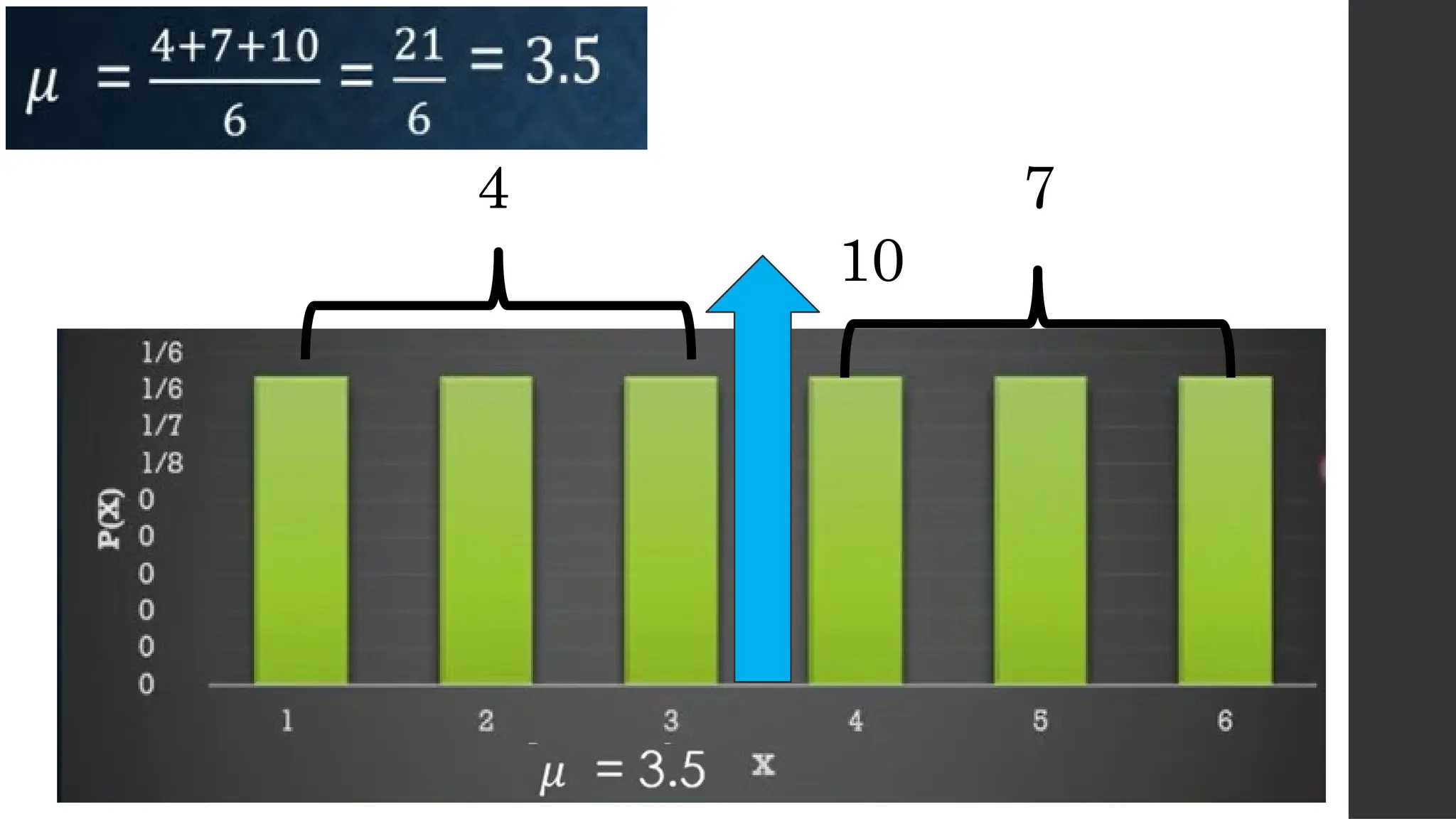
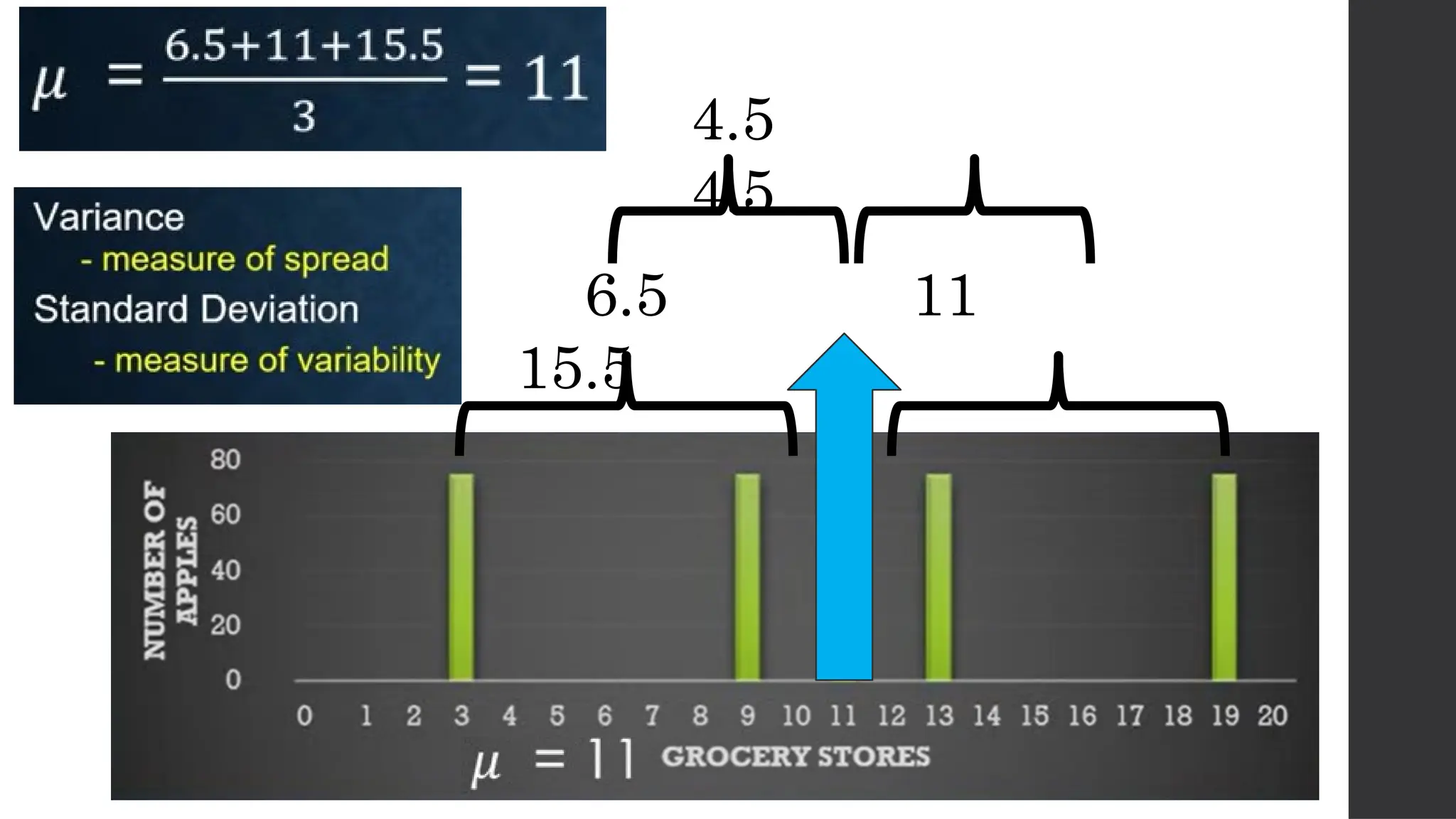
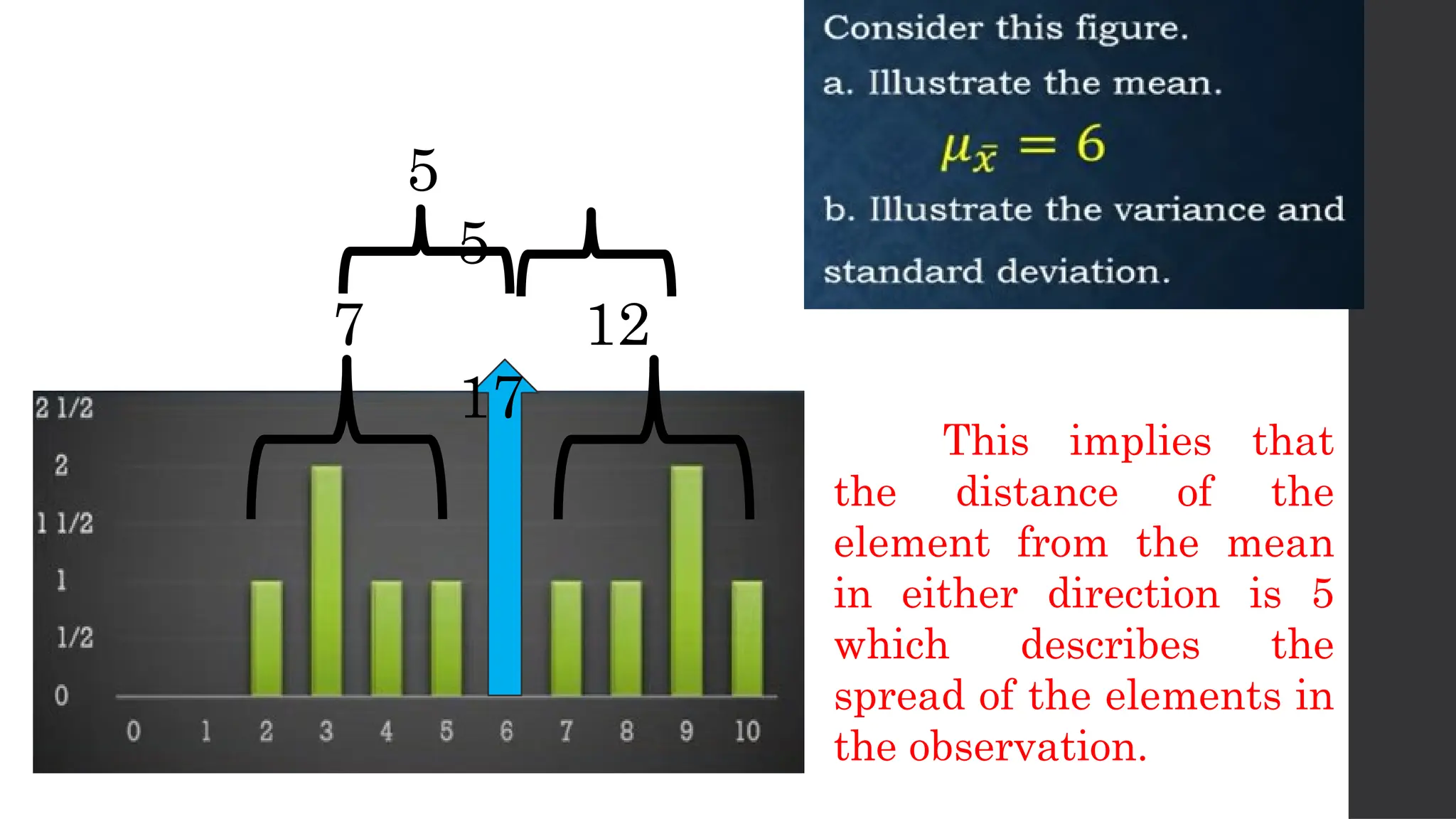
The document discusses probability distributions related to random variables, with examples such as the sales of albums and member availability in a dance group. It covers the calculation of mean and variance for discrete random variables, emphasizing their significance in determining the central location and spread of data. Key points include probability tables for specific scenarios and methods to compute expected values.

1. Computing Probability
Corresponding to a
given Random Variable
January 09, 2025
Melanie Ventura
Statistics and Probability

2. INEQUALITY SYMBOLS

3. Example:
The table shows the probabilities for the number of Red
Velvet albums sold in a given day at a merchandise store.
Number of
Albums (X)
Probability
P(X)
0 0.040
1 0.060
2 0.080
3 0.090
4 0.140
5 0.280
6 0.380
7 0.385
Find P(3

4. In a K-Pop dance group called NCT, the number of
members that are busy in their individual activities at
8:00 am from weekends. The probability shows in the
table.
What is the probability
that at least three, but
fewer than six of the
members of NCT are
busy at 8:00 am?
No. of
Members (X)
Probability,
P(X)
0 0.35
1 0.215
2 0.110
3 0.320
4 0.180
5 0.575
6 0.95

5. Let x be the value of a random variable represented by
the number of “Photocards” (PC) in an album. The
probability distribution table is shown in the table.
Find the probability
that at least 25 PCs can
be found in an album on
a particular day.
No. of PC
(X)
Probability
P(X)
12 3/12
21 1/12
25 2/12
32 1/6
40 3/12
47 2/12

6. Illustrating Mean
and Variance of
Discrete Random
Variable

7. The mean of a discrete random variable by utilizing
probabilities from its dispersion, as follows.
1. The mean is considered as a measure of the ‘ central location’
of a random variable. It is the weighted average of the values
that random variable X can take, with weights provided by
the probability distribution.
2. The Expected Value or Mean Value of a discrete random
variable x is can be computed by first multiplying each
possible x value by the probability of observing that value and
then adding the resulting quantities. Symbolically,

8. The average tends to be close to 3.5. this also implies
that the more rolls we do, the closer the average will be
to 3.5.

9. 4 7
10

10. 6.5 11
15.5
4.5
4.5

11. The variance for a random variable of a
probability distribution is
the standard deviation for a random variable of
a probability distribution is

12. 7 12
17
5
5
This implies that
the distance of the
element from the mean
in either direction is 5
which describes the
spread of the elements in
the observation.