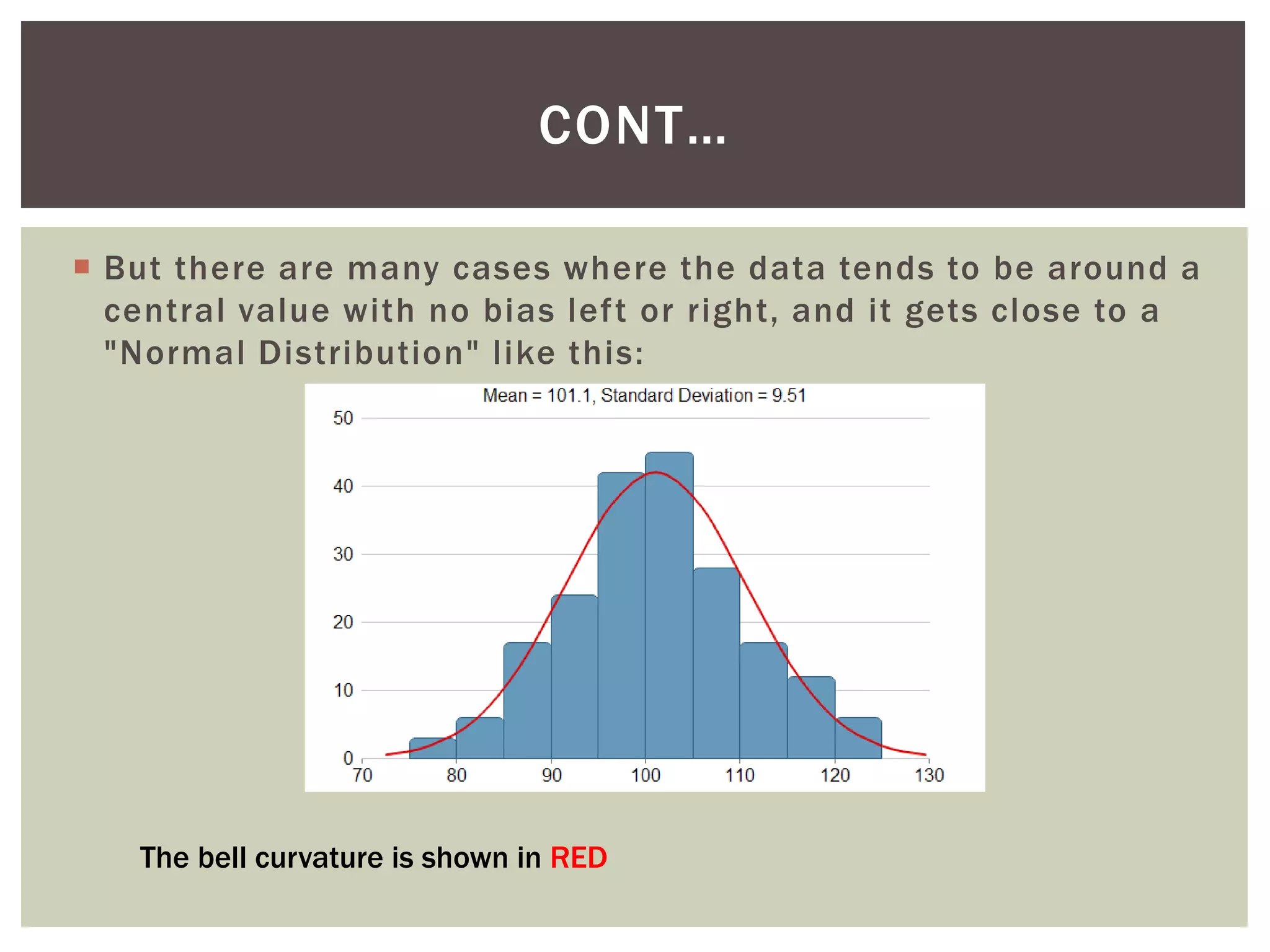
This document provides an overview of the normal distribution. It discusses how the normal distribution arises from the binomial distribution with large numbers of trials. Some key properties of the normal distribution are that it is symmetric, bell-shaped, and defined by its mean and standard deviation. The normal distribution is widely used in fields like statistics, science, engineering, and medicine. Examples are provided to demonstrate how to calculate probabilities within a normal distribution for applications like predicting machine part sizes and light bulb lifetimes.

1. BY
10- RISHAL KASHYAP
NORMAL DISTRIBUTION
MAINTENANCE AND RELIABILITY COURSE
PROF. HIMANSHU GUPTA
NATIONAL INSTITUTE OF TECHNOLOGY, SRINAGAR

2. Birth from Binomial Distribution ( Extremely
hectic and time consuming )
If a coin is flipped 100 times what is the
probability of getting more than 60 heads !
Tedious isn’t it !?
HISTORICAL BACKGROUND

3. CONT…
1. 18th century mathematician and statistician ..and a famous consultant to gamblers
2. Noted when number of flips of coins increases , the shape of binomial curve become
Smooth.
3. Curve came to known as Normal Curve

4.  All natural phenomenon are at least approximately Normal
distributed
 One of the first applications of the normal distribution the
analysis of errors of measurement made in astronomical
observations, errors occurred because of imperfect
instruments and imperfect observers!
 Measurements, Survey data on parameters, natural data, Size
of things produced by machines, errors in manufacturing etc.
CONT…

5.  Laplace, Gauss etc. given their input to understand
 The Simple Normal Curve lead to extensive study
 Birth of Gaussian or Laplace-Gaussian Distribution model
(Normal distribution)
 Wide range of applications in Stats, Natural Science,
Engineering, Social Science, Medical Science and what not
 IT IS MOST IMPORTANT IN ALL PROBABILITY DISTRIBUTIONS!
CONT…

6. THEORY
LEFT SPREADING RIGHT SPREADING
JUMBLED UP
Different types of spread of data

7.  But there are many cases where the data tends to be around a
central value with no bias left or right, and it gets close to a
"Normal Distribution" like this:
CONT…
The bell curvature is shown in RED

8.  The normal distribution is a family of distributions
f (x) = 1 √ (2πσ^2) e − (x−µ)^2/ 2σ^2
The Standard Normal has µ = 0 and σ = 1, i.e.
f (x) = 1 √ (2π e) (x^2/2)
Changing µ changes the location of the curve, and changing σ
changes the spread of the curve.
Continuous Probability Distribution
CONT…

9.  The Normal Distribution has
 mean = median = mode
 symmetry about the centre
 50% of values less than the mean
and 50% greater than the mean (TOTAL AREA UNDER CURVE IS
1.0)
CONT…

10. CONT…
STANDARD DEVIATIONS
The Standard Deviation is a measure of how spread out numbers are
68% of values are within
1 standard deviation of the mean
95% of values are within
2 standard deviations of the mean
99.7% of values are within
3 standard deviations of the mean

11.  It is good to know the standard deviation, because we can
say that any value is:
 likely to be within 1 standard deviation (68 out of 100
should be)
 very likely to be within 2 standard deviations (95 out of
100 should be)
 almost certainly within 3 standard deviations (997 out of
1000 should be)
CONT…
The no. of standard
deviations fro means
is known as “Z score”

12. CONT…
1. z is the z score ( standard score)
2. X is the value to be standardized
3. μ is the mean
4. σ is the standard deviation
We do standardization to make calculation easy because we have tables
For standard distribution so we don’t have to do calculate for each mean
and sigma. Life is easy now !

13. CONT…
Standard Normal Distribution Curve ( we have all the values in table )

14. CONT…
1. Disciplined, Statistical-based, data-driven approach
2. Developed by Motorola in early 1980s
3. Measure of process performance,
with Six Sigma being the goal,
based on the defects per million

15. CONT…
Very important concept in Manufacturing systems technology and quality
control !

16.  Used in every fields of science and engineering
 In Mechanical and Industrial Engineering
a. In Production Systems Technology
b. In Quality Control and Optimization etc.
APPLICATIONS AND EXAMPLES

17.  A city installs 2000 electric lamps, having a mean burning life
of 1000 hours with a standard deviation of 200 hours. The
normal distribution is a close approximation to this case. a)
What is the probability that a lamp will fail in the first 700
burning hours?
Sol.
z1 = (x1 − µ)/(σ) = (700 −1000)/(200) =− 1.50 From standard
Z table, for z1 = –1.50 = (–1.5) + (–0.00),
Pr [X < 700] = Pr [Z < –1.50] = Φ(–1.50) = 0.0668
Then Pr [burning life < 700 hours] = 0.0668 or 0.067.
b) What is the probability that a lamp will fail between 900 and
1300 burning hours?
EXAMPLE 1

18. z1 = (x1-μ)/(σ) = 900-1000/200 = -0.50 = -0.50 + -0.00
AND z2= (x2-μ)/(σ) = 1300-1000/200 = +1.50+ -0.00
Φ(z1) = Φ(–0.50) = 0.3085 and Φ(z2) = Φ(1.50) = 0.9332
Then Pr [900 hours < burning life < 1300 hours]
= Φ(z2) – Φ(z1) for = 0.9332 – 0.3085 = 0.6247 or 0.625.
CONT…

19.  A machine produces bolts which are (4,0.09), where
measurements are in mm. Bolts are measured accurately and
any which are smaller than 3.5mm or larger than 4.4mm is
rejected. Out of batch of 500 bolts, how many are acceptable?
Sol. P(X>4.4) = Φ[(4.4-4)/(0.3)] = Φ(1.33) = 0.90824
P(X<3.5) = Φ[(3.5-4)/(0.3)] = Φ(-1.67) = 0.04746
Hence P(3.5<X<4.4) = 0.90824-0.004746
= 0.86078
The number of acceptable items are therefore = 0.86078*500
=430.39
=430 (rounded
up) ANS.
EXAMPLE 2

20. CONCLUSION
NORMAL
DISTRIBUTION
Highly
applicable
in
research
Important
tool in TPM
Most
important
Probabilit
y
distributio
n
t, f and chi-
square test
is based on
the normal
distribution.

22.  WWW.MANAGEMENTEDUCATION.COM
 WWW.STUDYSTATS.COM
 WWW.EASYMATHS.COM
 VIRGINIA STATE UNIVERSITY
 WWW.UPLIFTEDUCATION.ORG
 WWW.CIMT.ORG
REFERENCES