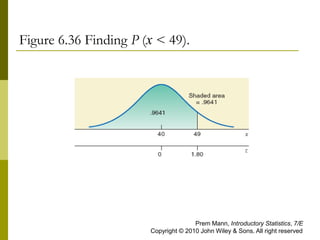
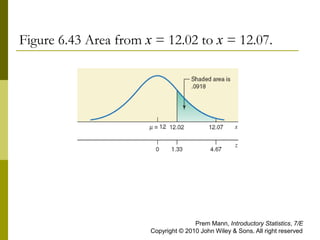
This document contains examples and solutions for problems involving the normal distribution. It begins with an example that converts x-values to z-values using the formula z = (x - μ)/σ. Several examples then demonstrate finding probabilities associated with various z-values. The document concludes with examples applying the normal distribution to real-world contexts like credit card debt, assembly times, soda filling, and product lifespans.