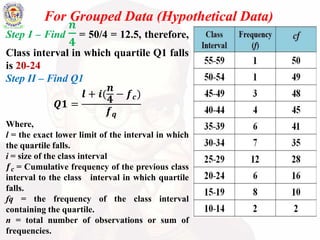
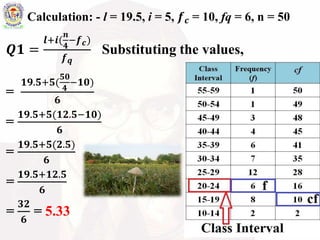
The document explains the concept of quartile and quartile deviation, with quartiles used to divide a data set into four equal parts. The quartile deviation is defined as half the difference between the first quartile (Q1) and the third quartile (Q3), serving as a measure of dispersion in the data set. The text also includes methods for calculating quartile deviation for both ungrouped and grouped data.

1. Quartile Deviation
Dr Rajesh Verma
Asst. Prof (Psychology)
Govt. College Adampur, Hisar, Haryana

2. Quartile: Meaning
One of the three points that divide a data set into
four equal parts. Or the values that divide data into
quarters. Each group contains equal number of
observations
or data.
Median acts
as base for
calculation
of quartile.

3. Quartile Deviation: Definition
The quartile deviation is half of the difference between
first quartile (Q1) and third quartile (Q3). This is also known as
quartile coefficient of dispersion.
QD =
𝑸𝟑−𝑸𝟏
𝟐
“A measure of dispersion that is defined as the value
halfway between the first and third quartiles (i.e., half the
interquartile range). Also called semi-interquartile range” (APA).
Garret (2014) defines, “the Quartile deviation or Q is half
the scale distance between 75th and 25th percent is a frequency
distribution”.
According to Guilford (1963) the
Semi inter Quartile range Q is the one
half the range of the middle 50 percent
of the cases.

4. Explanation
So, this way we have three quartiles i.e. Q1, Q2 and Q3.
(i) Q1 – It is the midpoint of lowest 50% of data and also
known as Lowest quartile or first quartile.
(ii) Q2 – It is the median of the data or the middle point of a
given data set and also known as second quartile.
(iii) Q3 – It is the midpoint of highest 50% of data and also
known as highest quartile or third quartile.
Thus the quartile
measures the dispersion of
score above and below the
median by dividing the
entire data set into
four equal groups.

5. Introduction
Any data set that meets the assumptions of normal
distribution tends to have maximum number of values in
the middle. It’s a kind of half of the range of middle 50%
data and also known as Semi inter-quartile range. Quartile
deviation (Q) is absolute measure of dispersion of the
central or middle portion of the
data set.
Important Note: The students must
understand the difference between
Quartile and Quarter. Quartile is
a point on a data set where as
Quarter is 1/4th part. You can
be in a quarter but you have
to be at a quartile.

6. Characteristics of QD
1. Median is base of the quartile deviation.
2. Quartile deviation is not affected with extreme values.
3. In a symmetrical distributions Q1 and Q3 are at
equal distance from the median (Median-Q1=Q3-Median).
4. QD is the best measure of variability for open ended
distribution.
5. Quartiles are three points on the distribution that
divides the
distribution
into 4 quarters.

7. 6. The Q1 and Q3 are lower and upper limits of
middle 50% distribution.
7. It is the index of score density at the middle of
distribution.
8. The larger the variability in a distribution the
larger the value of Q and vice-versa.
9. In normal distribution Quartile distribution (Q) is
called
probability
error (PE).

8. Computation of QD
For Ungrouped Data(Hypothetical data)
(i) If data is in odd number
Ex – 12, 54, 32, 51, 24, 60, 21, 44, 31, 48, 50
Step I – Arrange the raw data in ascending order.
Therefore, 12, 21, 24, 31, 32, 44, 48, 50, 51, 54, 60
Step II – Find out Q1
Q1 =
𝑵+𝟏
𝟒
th position
in the ordered
distribution.
therefore,
Q1=11+1/4
= 3rd position i.e. 24

9. (12, 21, 24, 31, 32, 44, 48, 51, 54, 60)
Step III – Find out Q3
Q3 =
𝑵+𝟏 𝟑
𝟒
th position in the ordered distribution.
therefore, Q3 = (11+1)3/4 = 9th position i.e. 51
Step IV – Find out Semi-quartile range or QD
Q =
𝑸𝟑−𝑸𝟏
𝟐
therefore,
=
𝟓𝟏−𝟐𝟒
𝟐
= 27/2= 13.5

10. Computation of QD
For Ungrouped Data(Hypothetical data)
(i) If data is in even number
Ex – 12, 54, 32, 51, 24, 60, 21, 44, 31, 48
Step I – Arrange the raw data in ascending order.
Therefore, 12, 21, 24, 31, 32, 44, 48, 51, 54, 60
Step II – Find out Q1
Q1 =
𝑵+𝟏
𝟒
th position in the ordered distribution.
therefore, Q1=11/4 = 2.75th position i.e.
2nd obs + .75 (3rd obs -2nd obs),
21+.75(24-21) = 21+ 1.5 = 22.5

11. (12, 21, 24, 31, 32, 44, 48, 50, 51, 54, 60)
Step III – Find out Q3
Q3 =
𝑵+𝟏 𝟑
𝟒
th position in the ordered distribution.
therefore, Q3 = (10+1)3/4 = 8.25th position i.e.
8th obs + .25(9th obs – 8th obs) = 51+.25(54-51)
= 51+.25(3) => 51+.75 = 51.75
Step IV – Find out Semi-quartile range or QD
Q =
𝑸𝟑−𝑸𝟏
𝟐
therefore,
𝟓𝟏.𝟕𝟓−𝟐𝟐.𝟓
𝟐
= 29.25/2
= 14.625

12. For Grouped Data (Hypothetical Data)
Step I – Find
𝒏
𝟒
= 50/4 = 12.5, therefore,
Class interval in which quartile Q1 falls
is 20-24
Step II – Find Q1
𝑸𝟏 =
𝒍 + 𝒊(
𝒏
𝟒
− 𝒇 𝒄)
𝒇 𝒒
Where,
l = the exact lower limit of the interval in which
the quartile falls.
i = size of the class interval
𝒇 𝒄 = Cumulative frequency of the previous class
interval to the class interval in which quartile
falls.
fq = the frequency of the class interval
containing the quartile.
n = total number of observations or sum of
frequencies.

13. Calculation: - l = 19.5, i = 5, 𝒇 𝒄 = 10, fq = 6, n = 50
𝑸𝟏 =
𝒍+𝒊(
𝒏
𝟒
−𝒇 𝒄)
𝒇 𝒒
Substituting the values,
=
𝟏𝟗.𝟓+𝟓(
𝟓𝟎
𝟒
−𝟏𝟎)
𝟔
=
𝟏𝟗.𝟓+𝟓(𝟏𝟐.𝟓−𝟏𝟎)
𝟔
=
𝟏𝟗.𝟓+𝟓(𝟐.𝟓)
𝟔
=
𝟏𝟗.𝟓+𝟏𝟐.𝟓
𝟔
=
𝟑𝟐
𝟔
= 5.33

14. Step III – Find
𝟑𝒏
𝟒
=
𝟑𝐱𝟓𝟎
𝟒
= 150/4 = 37.5
therefore, Class interval in which quartile Q3 falls
is 35-39
Step IV – Find Q3 with the following formula
𝑸𝟑 =
𝒍 + 𝒊(
𝟑𝒏
𝟒
− 𝒇 𝒄)
𝒇 𝒒

15. Calculation: - l = 34.5, i = 5, 𝒇 𝒄 = 35, fq = 6, n = 50
Q𝟑 =
𝒍+𝒊(
𝟑𝒏
𝟒
−𝒇 𝒄)
𝒇 𝒒
Substituting the values,
=
𝟑𝟒.𝟓+𝟓(
𝟑(𝟓𝟎)
𝟒
−𝟑𝟓)
𝟔
=
𝟑𝟒.𝟓+𝟓(𝟑𝟕.𝟓−𝟑𝟓)
𝟔
=
𝟑𝟒.𝟓+𝟓(𝟐.𝟓)
𝟔
=
𝟑𝟒.𝟓+𝟏𝟐.𝟓
𝟔
=
𝟒𝟕
𝟔
= 7.83

16. Substituting the values in the formula,
𝑸 𝒐𝒓 𝑸𝑫 =
𝑸𝟑−𝑸𝟏
𝟐
=
𝟕.𝟖𝟑−𝟓.𝟑𝟑
𝟐
=
𝟐.𝟓
𝟐
= 1.25
So, our quartile deviation of our hypothetical
grouped data is 1.25.

17. References:
1. https://dictionary.apa.org/quartile-deviation.
2. Guilford, J. P. and Fruchter, B. (1978). Fundamental Statistics in
Psychology and Education, 6th ed. Tokyo: McGraw-Hill.
3. https://todayinsci.com/M/Mahalanobis_Prasanta/
MahalanobisPrasanta-Quotations.htm.
4. Garrett, H. E. (2014). Statistics in Psychology and Education. New
Delhi: Pragon International.
5. Levin, J. & Fox, J. A.
(2006). Elementary Statistics.
New Delhi: Pearson.

18. vermasujit@yahoo.com
Next
Discussion
Standard Deviation