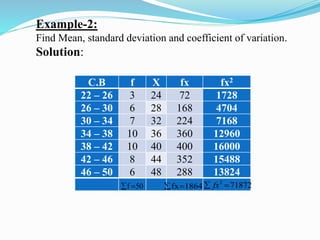
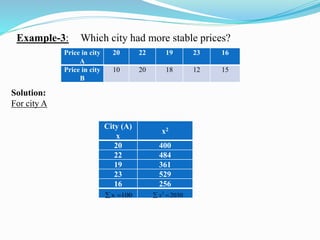
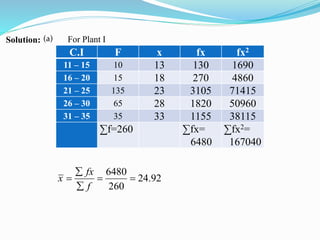
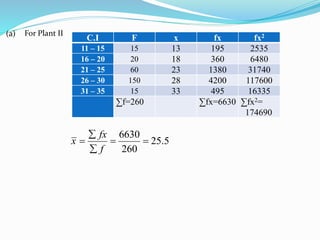
The document defines and provides examples for calculating the coefficient of variation, which is a measure used to compare the dispersion of data sets. It gives the formula for coefficient of variation as the standard deviation divided by the mean, expressed as a percentage. Two examples are shown comparing the stability of prices between two cities and production between two manufacturing plants, with the data set having the lower coefficient of variation considered more consistent or stable.

1. NADEEM UDDIN
ASSOCIATE PROFESSOR
OF STATISTICS

2. Coefficient of Variation
1. Coefficient of Variation is a relative measure of dispersion.
2. Coefficient of Variation is useful in comparing the variability of two
or more sets of data. The one which has less Coefficient of Variation
is considered more consistent in the performance.
3. Coefficient of Variation is expressed as a percentage.
4. Coefficient of Variation indicates that the standard deviation is as a
percent of the mean.
Coefficient of Variation =
Standard deviation
𝑀𝑒𝑎𝑛
× 100

3. Example-1: For the data 2, 4, 6, 8 and 10
Find (a) Mean and Standard deviation.
(b) Coefficient of Variation
Solution:
X
x2
2 4
4 16
6 36
8 64
10 100
30x  220x2


4. 22
2
30
( ) 6
5
.
220 30
5 5
44 36
8
x
a x
n
x x
S D
n n



  
  
    
 
 
   
 
 

2.82 
2.82
( ) . 100 100 47%
6
b CV
x

    

5. C.B f X fx fx2
22 – 26 3 24 72 1728
26 – 30 6 28 168 4704
30 – 34 7 32 224 7168
34 – 38 10 36 360 12960
38 – 42 10 40 400 16000
42 – 46 8 44 352 15488
46 – 50 6 48 288 13824
50f  1864fx
2
71872fx 
Example-2:
Find Mean, standard deviation and coefficient of variation.
Solution:

6. 22
2
1864
37.28
50
71872 1864
6.90
50 50
6.90
. 100 100 18.51%
37.28
fx
x
f
fx fx
f f
CV
x



  

  
   
  
 
   
 
    

7. Example-3: Which city had more stable prices?
Price in city
A
20 22 19 23 16
Price in city
B
10 20 18 12 15
Solution:
For city A
City (A)
x
x2
20 400
22 484
19 361
23 529
16 256
100x  2
2030x 

8. 2 22
100
20
5
2030 100
5 5
2.45
2.45
. .( ) 100 100
20
12.25%
x
x
n
x x
n n
CV A
x




  
    
      
   

   


9. For city B City (B)
x
x2
10 100
20 400
18 324
12 144
15 225
75x  1931x2

2 22
75
15
5
1931 75
5 5
x
x
n
x x
n n


  
    
      
   
3.69
3.69
. .( ) 100 100
15
24.6%
C V B
x



   

Since C.V (A) < C.V (B). Therefore City A had more stable prices.

10. Example-4:
A manufacturing company owns two plants which manufacture the
same product. The weekly output of the two plants for the past 5
years was as follows:
Weekly
Output
(in 1000
units)
Number of Weeks
Plant I Plant II
11 – 15 10 15
16 – 20 15 20
21 – 25 135 60
26 – 30 65 150
31 – 35 35 15
a. Calculate coefficient of variation for the two plants.
b. Which plant gives more stable production?

11. Solution: For Plant I
C.I F x fx fx2
11 – 15 10 13 130 1690
16 – 20 15 18 270 4860
21 – 25 135 23 3105 71415
26 – 30 65 28 1820 50960
31 – 35 35 33 1155 38115
∑f=260 ∑fx=
6480
∑fx2=
167040
6480
24.92
260
fx
x
f

  

(a)

12. 22
fx fx
f f

  
  
  
2
167040 6480
260 260

 
  
 
642.46 621.16  
21.30
4.62




. ( ) 100c v I
x

 
C.V (I) %54.18100
92.24
62.4

(b)

13. For Plant II
C.I F x fx fx2
11 – 15 15 13 195 2535
16 – 20 20 18 360 6480
21 – 25 60 23 1380 31740
26 – 30 150 28 4200 117600
31 – 35 15 33 495 16335
∑f=260 ∑fx=6630 ∑fx2=
174690
6630
25.5
260
fx
x
f

  

(a)

14. 22
2
174690 6630
260 260
671.88 650.25
21.63
4.65
fx fx
f f





  
  
  
 
  
 
 


. ( ) 100c v II
x

 
C.V (II) %24.18100
5.25
65.4

Since C.V (II) < C.V (I)
Therefore Plant II gives more stable production.
(b)