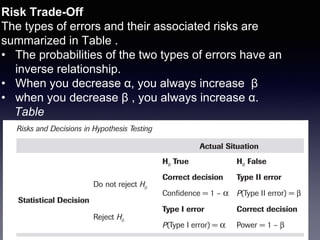
The document discusses hypothesis testing, including defining the null and alternative hypotheses, types of errors, test statistics, and the process of hypothesis testing. Some key points: - The null hypothesis states that a population parameter is equal to a specific value. The alternative hypothesis is paired with the null and states inequality. - Type I errors occur when the null hypothesis is rejected when it is true. Type II errors occur when the null is not rejected when it is false. 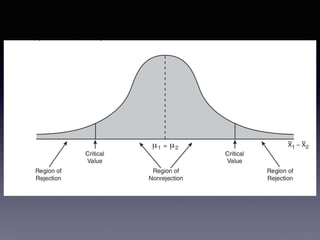- A test statistic is calculated based on sample data and compared to critical values to determine if the null hypothesis can be rejected. - Hypothesis testing follows steps of stating hypotheses, choosing a significance level, collecting/analyzing data,

1. Hypothesis Testing
Assignment
By
Dr.Myo Naing (RN-19), Dr.Aung Ko Ko Win(RN-35)

2. Hypothesis
• A statement about one or more population
• Types of hypothesis
-Research hypothesis : the conjecture or
supposition that motivates the research
-Statistical hypothesis : hypothesis that are
stated in such away that they may be evaluated by
appropriate statistical techniques

3. Null Hypothesis (symbol H 0)
The statement that a population parameter is equal to a
specific value or that the population parameters from two
or more groups are equal.
eg.“the mean height for women is the same as the mean
height for men,
INTERPRETATION
• is always expresses an equality and is always paired
with another statement, the alternative hypothesis.
• is considered true until evidence indicates otherwise.
• If you can conclude that the null hypothesis is false,
then the alternative hypothesis must be true.

4. Alternative Hypothesis (symbol H 1) (HA)
The statement paired with a null hypothesis that is
mutually exclusive to the null hypothesis.
eg.“the mean height for women is not the same as the
mean height for men” (paired with the example for
the null hypothesis)
INTERPRETATION
• is typically the idea you are studying concerning your
data
• is always expresses an inequality, either between a
population parameter and a specific value or between
two or more population parameters
• is always paired with the null hypothesis

5. Important points
• represents the conclusion reached by rejecting the null
hypothesis.
• reject the null hypothesis if evidence from the sample
statistic indicates that the null hypothesis is unlikely to be
true.
• if you cannot reject the null hypothesis, you cannot claim
to have proven the null hypothesis.
• Failure to reject the null hypothesis means (only) that you
have failed to prove the alternative hypothesis.

6. Test Statistic
The value based on the sample statistic and the sampling
distri- bution for the sample statistic.
e.g.
(1)Test statistic for the difference between two sample
means,
(2) test statistic for the difference between two sample
proportions,
(3)test statistic for the difference between the means of
more than two groups

7. INTERPRETATION
• If you are testing whether the mean of a population
was equal to a specific value, the sample statistic is
the sample mean.
• The test statistic is based on the difference between
the sample mean and the value of the population mean
stated in the null hypothesis.
• This test statistic follows a statistical distribution called
the t distribution.

8. • If you are testing whether the mean of population one is
equal to the mean of population two, the sample statistic is
the difference between the mean in sample one and the
mean in sample two.
• The test statistic is based on the difference between the
mean in sample one and the mean in sample two. This test
statistic also follows the t distribution.
• The sampling distribution of the test statistic is divided into
two regions, a region of rejection (also known as the
critical region) and a region of non-rejection.
• If the test statistic falls into the region of non rejection , the
null hypothesis is not rejected.

10. • The region of rejection contains the values of the test
statistic that are unlikely to occur if the null hypothesis is
true.
• If the null hypothesis is false, these values are likely to
occur.
• Therefore, if you observe a value of the test statistic that falls
into the rejection region, you reject the null hypothesis,
because that value is unlikely if the null hypothesis is true.
• To make a decision concerning the null hypothesis,
first determine the critical value of the test statistic that
separates the nonrejection region from the rejection region.
• the critical value by using the appropriate sampling
distribution and deciding on the risk you are willing to take of
rejecting the null hypothesis when it is true.

11. Practical Significance Versus Statistical
Significance
• Another issue in hypothesis testing concerns the
distinction between a statistically significant difference
and a practical significant difference
• Given a large enough sample size, it is always possible
to detect a statistically significant difference.
• This is because no two things in nature are exactly
equal. So, with a large enough sample size, you can
always detect the natural difference between two
populations.
• You need to be aware of the real-world practical
implications of the statistical significance.

12. Decision-Making Risks
In hypothesis testing, you always face the possibility
that either you will
wrongly reject the null hypothesis(Type I Error) or
wrongly not reject the null hypothesis(Type II Error).

13. Type I Error
The error that occurs if the null hypothesis H 0 is rejected
when it is true and should not be rejected.
CONCEPT
• The risk, or probability, of a type I error occurring is
identified by the Greek lowercase alpha, α ,Alpha is
also known as the level of significance of the statistical
test.
• Traditionally, you control the probability of a type I error
by deciding the risk level G you are willing to tolerate of
rejecting the null hypothesis when it is true.
• Because you specify the level of significance before
performing the hypothesis test, the risk of committing a
type I error, G, is directly under your control.

14. The most common α values are 0.01, 0.05, and 0.10,
and researchers traditionally select a value of 0.05 or
smaller.
INTERPRETATION
When you specify the value for α, you determine the
rejection region, and using the appropriate sampling
distribution, the critical value or values that divide the
rejection and nonrejection regions are determined.

15. Type II Error
The error that occurs if the null hypothesis H 0 is not
rejected when it is false and should be rejected.
INTERPRETATION
The risk, or probability, of a type II error occurring is
identified by the Greek lowercase beta, β.
The probability of a type II error depends on the size of
the difference between the value of the population
parameter stated in the null hypothesis and the actual
population value.

16. • Unlike the type I error, the type II error is not directly
established by you.
• Because large differences are easier to find, as the
difference between the value of the population
parameter stated in the null hypothesis and its
corresponding population parameter increases, the
probability of a type II error decreases.
• Therefore, if the difference between the value of the
population parameter stated in the null hypothesis and
the corresponding parameter is small, the probability
of a type II error
• represents the probability of rejecting the null
hypothesis when it is false and should be rejected.

17. Risk Trade-Off
The types of errors and their associated risks are
summarized in Table .
• The probabilities of the two types of errors have an
inverse relationship.
• When you decrease α, you always increase β
• when you decrease β , you always increase α.
Table

18. Performing Hypothesis Testing
When you perform a hypothesis test, you should follow the
steps of hypothesis testing in this order:
1. State the null hypothesis, H 0 , and the alternative
hypothesis, H 1
2. Evaluate the risks of making type I and II errors, and
choose the level of significance, α, and the sample size
as appropriate.
3. Determine the appropriate test statistic and sampling
distribution to use and identify the critical values that
divide the rejection and nonrejection regions.
4. Collect the data, calculate the appropriate test statistic,
and determine whether the test statistic has fallen into
the rejection or the nonrejection region.

19. 5. Make the proper statistical inference. Reject the null
hypothesis if the test statistic falls into the rejection
region. Do not reject the null hypothesis if the test statistic
falls into the nonrejection region.
The p-Value Approach to Hypothesis Testing
Most modern statistical software, including the functions
found in spread- sheet programs and calculators,
can calculate the probability value known as the p-value
that you can use as a second way of determining whether
to reject the null hypothesis.

20. p-Value
The probability of computing a test statistic equal to or more
extreme than the sample results, given that
the null hypothesis H 0 is true.
• The p-value is the smallest level at which H 0 can be
• rejected for a given set of data.
• Can consider the p-value the actual risk of having
• a type I error for a given set of data.

21. • Using p-values, the decision rules for rejecting the null
hypothesis are-
1. If the p-value is greater than or equal to α, do not reject
the null hypothesis.
2. If the p-value is less than α, reject the null
hypothesis.
3. Many people confuse this rule, mistakenly believing
that a high p-value is reason for rejection. You can
avoid this confusion by remembering the following
saying: “If the p-value is low, then H 0 must go.”

22. In practice, most researchers today use p-values for several
reasons, including efficiency of the presentation of results.
The p-value is also known as the observed level of
significance.
When using p-values, you can restate the steps of hypothesis
testing as follows:
1. State the null hypothesis, H 0 , and the alternative
hypothesis, H 1 .
2. Evaluate the risks of making type I and II errors, and
choose the level of significance, α, and the sample size as
appropriate.
3. Collect the data and calculate the sample value of the
appropriate test statistic.

23. 4. Calculate the p-value based on the test statistic and
compare the p- value to α.
5. Make the proper statistical inference. Reject the null
hypothesis if the p-value is less than α. Do not reject the
null hypothesis if the p-value is greater than or equal to α.

24. Types of Hypothesis Tests
Your choice of which statistical test to use when
performing hypothesis testing is influenced by the
following factors:
• Number of groups of data: one, two, or more than
two
• Relationship stated in alternative hypothesis H 1 :
not equal to or inequality (less than, greater than)
• Type of variable (population parameter):
numerical (mean) or categorical (proportion)

25. Relationship Stated in Alternative Hypothesis H 1
Alternative hypotheses can be stated either
using the not-equal sign, as in, H 1 : S 1 ≠ S 2 ; or
by using an inequality, such as H 1 : S 1 > S 2 .
You use a two-tail test for alternative hypotheses that
use the not-equal sign and use a one-tail test for
alternative hypotheses that contain an inequality.

26. THANK
YOU