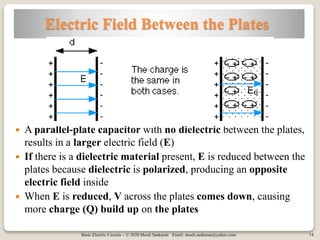
The document covers the basics of electric circuits with a focus on capacitors, explaining their charging process, properties, and construction parameters. It outlines how capacitance is calculated, the influence of dielectrics, and the behavior of electric fields and voltage within capacitors. Additionally, it discusses various types of capacitors and defines active and passive elements in circuit theory.