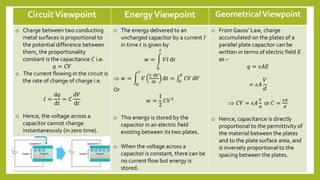
Passive circuit components include resistors, capacitors, and inductors. They can only receive, store, or dissipate energy from a circuit rather than supplying energy. Resistors limit current flow and dissipate energy as heat. Capacitors store electric charge and energy in an electric field. Inductors store energy in a magnetic field produced by current flowing through a coil. The key parameters are resistance (R) for resistors, capacitance (C) for capacitors, and inductance (L) for inductors.

1. PASSIVE CIRCUIT
COMPONENTS
Efforts By –
SAKSHAM KOUL

2. PASSIVE CIRCUIT COMPONENTS – WHAT?
 A passive component is an electronic component which can only receive energy,
which it can either dissipate, absorb or store it in an electric field or a magnetic field.
 Passive elements do not need any form of electrical power to operate.
 They are contrary in principle to the active circuit elements, which can be
understood as suppliers of energy in a circuit, such as a battery.
 For Example: Resistor, Capacitor, Inductor etc…

3. RESISTOR
 A resistor is a passive electrical component with the primary function to limit the
flow of electric current.
 The resistance of a resistor is its primary parameter. Resistance is expressed in
Ohms (Ω) and is dependent on the shape of the resistive part and the material
properties.
 A resistor is taken as a passive element since it can not deliver any energy to a
circuit. Instead a resistor can only receive energy which it can dissipate as heat as
long as current flows through it.

4. CircuitViewpoint EnergyViewpoint GeometricalViewpoint
o By Ohm’s Law, we have 𝑅 =
𝑉
𝐼
o Resistance of most metallic
conductors varies with
temperature.
𝑅2 = 𝑅1 1 + 𝛼 𝑇2 − 𝑇1
Where,
𝑅1 - Resistance at temperature 𝑇1
𝑅2 - Resistance at temperature 𝑇2
𝛼 –Temperature coefficient of
resistance
o It converts electrical energy
into heat energy.
𝑃 = 𝑉𝐼 = 𝐼𝑅 𝐼 = 𝐼2 𝑅
= Rate of energy absorbed
The corresponding amount of
energy converted to heat in the
time interval 𝑡2 − 𝑡1 is given by –
𝑤 =
𝑡1
𝑡2
𝐼2 𝑅 ⅆ𝑡
o For constant current, this takes
the form –
𝑤 = 𝐼2 𝑅𝑡
Where 𝑡 = 𝑡2 − 𝑡1
o 𝑅 = 𝜌
𝐿
𝐴
Where,
𝜌 – Resistivity / Specific resistance
of the material
𝐿 – Length of the conductor
𝐴 – Cross-sectional area
o Conductance is defined as the
reciprocal of resistance. It is
denoted by 𝐺 and is measured
in siemens.
𝐺 ≡
1
𝑅
Hence,
𝐺 =
1
𝜌
𝐴
𝐿
= 𝜎
𝐴
𝐿
𝜎 denotes conductivity and is the
reciprocal of resistivity.

5. CAPACITOR
 A capacitor in an electrical circuit behaves as a charge storage device. It holds the
electric charge when a voltage is applied across it, and it gives up the stored
charge to the circuit as and when required.
 A capacitor is considered as a passive element because it can store energy in it as
electric field. As such it is not considered an active component since no energy is
being supplied or amplified.
 The capacitance of a capacitor is its primary parameter. Capacitance is expressed
in Farads (F).

6. CircuitViewpoint EnergyViewpoint GeometricalViewpoint
o Charge between two conducting
metal surfaces is proportional to
the potential difference between
them, the proportionality
constant is the capacitance 𝐶 i.e.
𝑞 = 𝐶𝑉
o The current flowing in the circuit is
the rate of change of charge i.e.
𝐼 =
ⅆ𝑞
ⅆ𝑡
= 𝐶
ⅆ𝑉
ⅆ𝑡
o Hence, the voltage across a
capacitor cannot change
instantaneously (in zero time).
o The energy delivered to an
uncharged capacitor by a current 𝐼
in time 𝑡 is given by
𝑤 =
0
𝑡
𝑉𝐼 ⅆ𝑡
 𝑤 =
0
𝑡
𝑉
𝐶 ⅆ𝑉
ⅆ𝑡
ⅆ𝑡 = 0
𝑉
𝐶𝑉 ⅆ𝑉
Or
𝑤 =
1
2
𝐶𝑉2
o This energy is stored by the
capacitor in an electric field
existing between its two plates.
o When the voltage across a
capacitor is constant, there can be
no current flow but energy is
stored.
o From Gauss’ Law, charge
accumulated on the plates of a
parallel plate capacitor can be
written in terms of electric field 𝐸
as –
𝑞 = 𝜖𝐴𝐸
= 𝜖𝐴
𝑉
ⅆ
 𝐶𝑉 = 𝜖𝐴
𝑉
𝑑
or 𝐶 =
𝜖𝐴
𝑑
o Hence, capacitance is directly
proportional to the permittivity of
the material between the plates
and to the plate surface area, and
is inversely proportional to the
spacing between the plates.

7. INDUCTOR
 An inductor is an energy storage device which stores energy in the form of
magnetic field when electric current flows through it.
 An inductor is also considered as a passive element of circuit, because it can store
energy in it as magnetic field.
 Due to the property of induced emf, all types of electrical coils can be referred to
as inductors.
 The inductance of an inductor is its primary parameter. Inductance is expressed in
Henry (H).

8. CircuitViewpoint EnergyViewpoint GeometricalViewpoint
o The induced emf across a coil is
directly proportional to the rate of
change of current through it, the
proportionality constant is
inductance 𝐿 i.e.
𝑉 = 𝐿
ⅆ𝐼
ⅆ𝑡
⇒ 𝐿 =
𝑉
ⅆ 𝐼 ⅆ 𝑡
o Hence, the current in an inductor
cannot change abruptly in zero
time.
o The energy delivered to an
inductor having zero initial current
by a current 𝐼, in time 𝑡 is given by
𝑤 =
0
𝑡
𝑉𝐼 ⅆ𝑡
 𝑤 =
0
𝑡
𝑉
L ⅆ𝐼
ⅆ𝑡
ⅆ𝑡 = 0
𝐼
L𝐼 ⅆ𝐼
Or
𝑤 =
1
2
𝐿𝐼2
o This energy is stored in the form
of a magnetic field existing inside
the inductor.
o A constant current results in a
zero voltage drop across the ideal
inductor, but energy can still be
stored in its magnetic field.
o Using Faraday’s law of EMI,
𝑉 = 𝐿
ⅆ𝐼
ⅆ𝑡
= 𝑁
ⅆ𝜙
ⅆ𝑡
 𝐿 = 𝑁
ⅆ𝜙
ⅆ𝐼
o Now,
𝜙 =
𝑚𝑚𝑓
𝑚𝑎𝑔𝑛𝑒𝑡𝑖𝑐 𝑟𝑒𝑙𝑢𝑐𝑡𝑎𝑛𝑐𝑒
=
𝑁𝐼
𝑅
And
𝑅 =
𝑙
𝜇𝐴
Hence,
𝐿 =
𝑁2 𝜇𝐴
𝑙
Where,
𝑙 – Mean core length
𝐴 – Cross-sectional area
𝑁 – Number of turns in the coil
𝜇 – Magnetic permeability of core