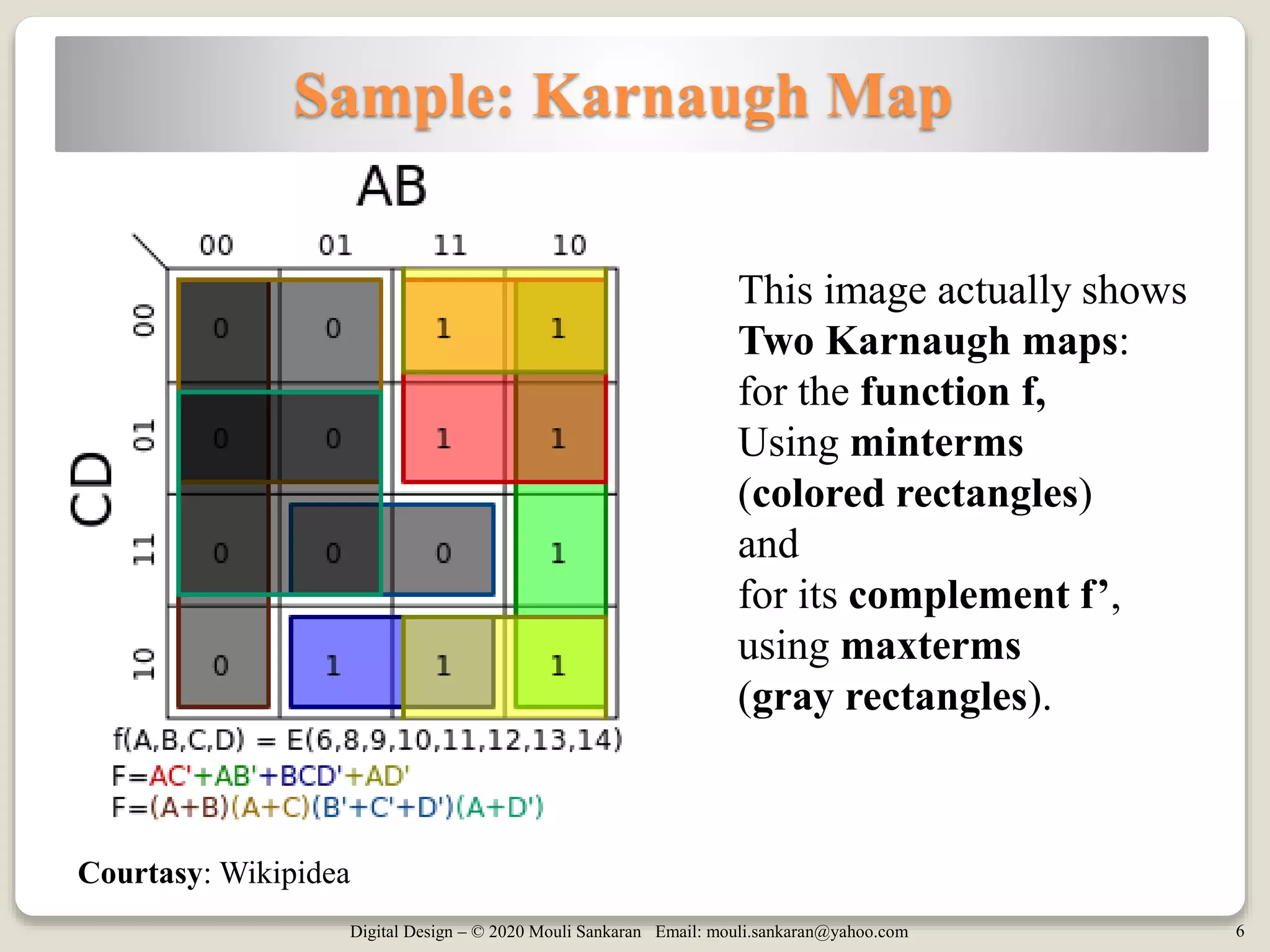
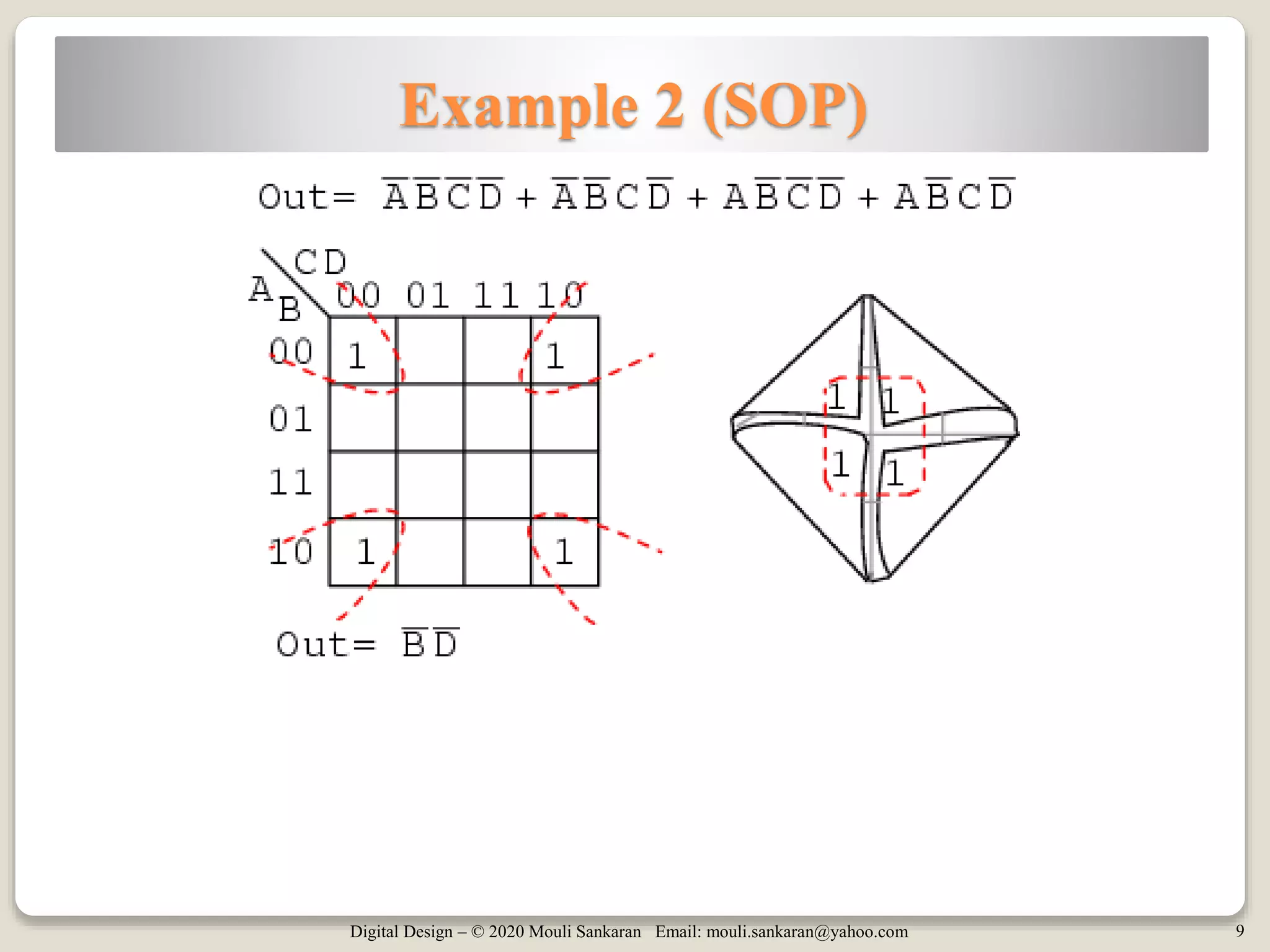
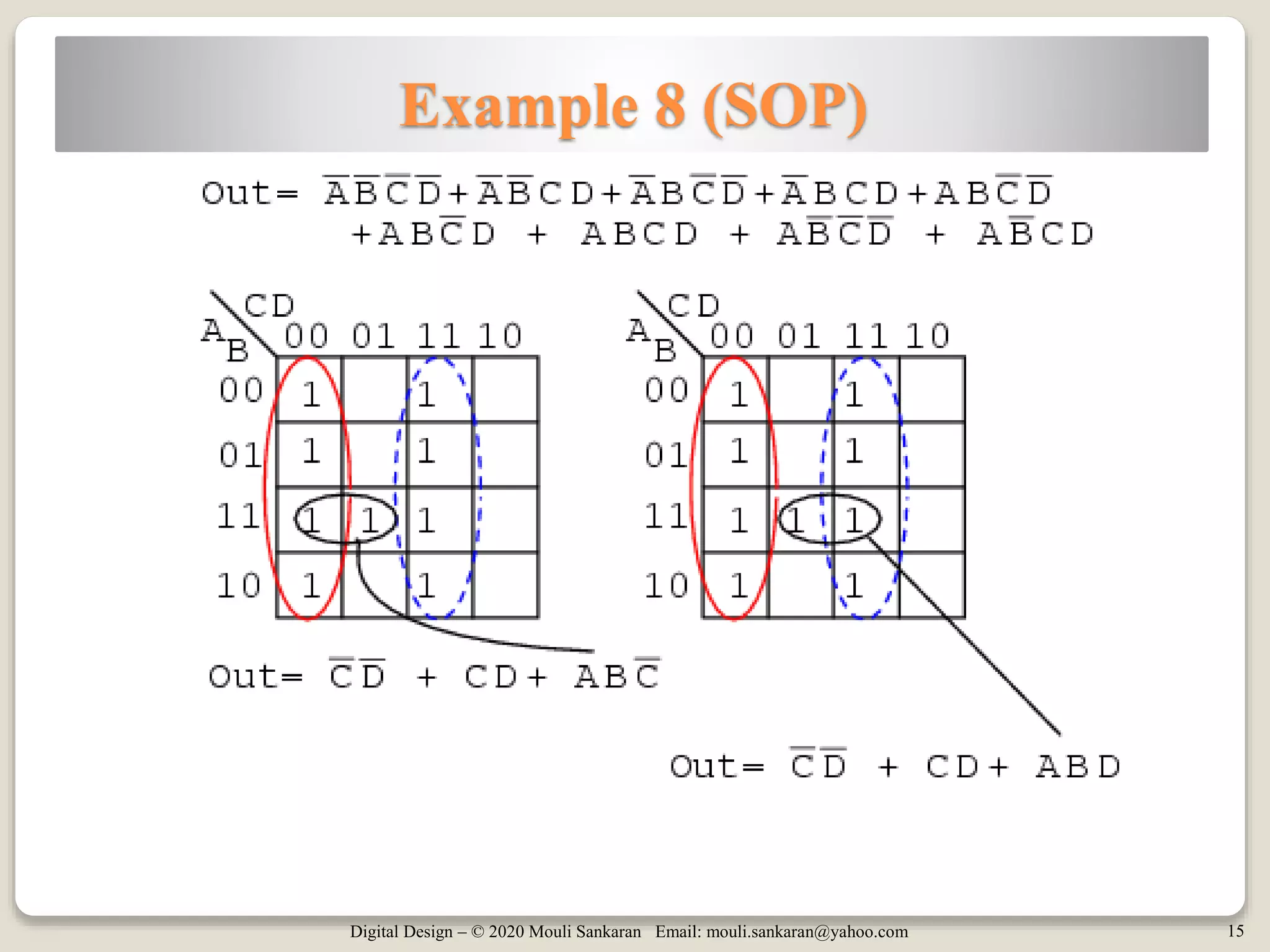
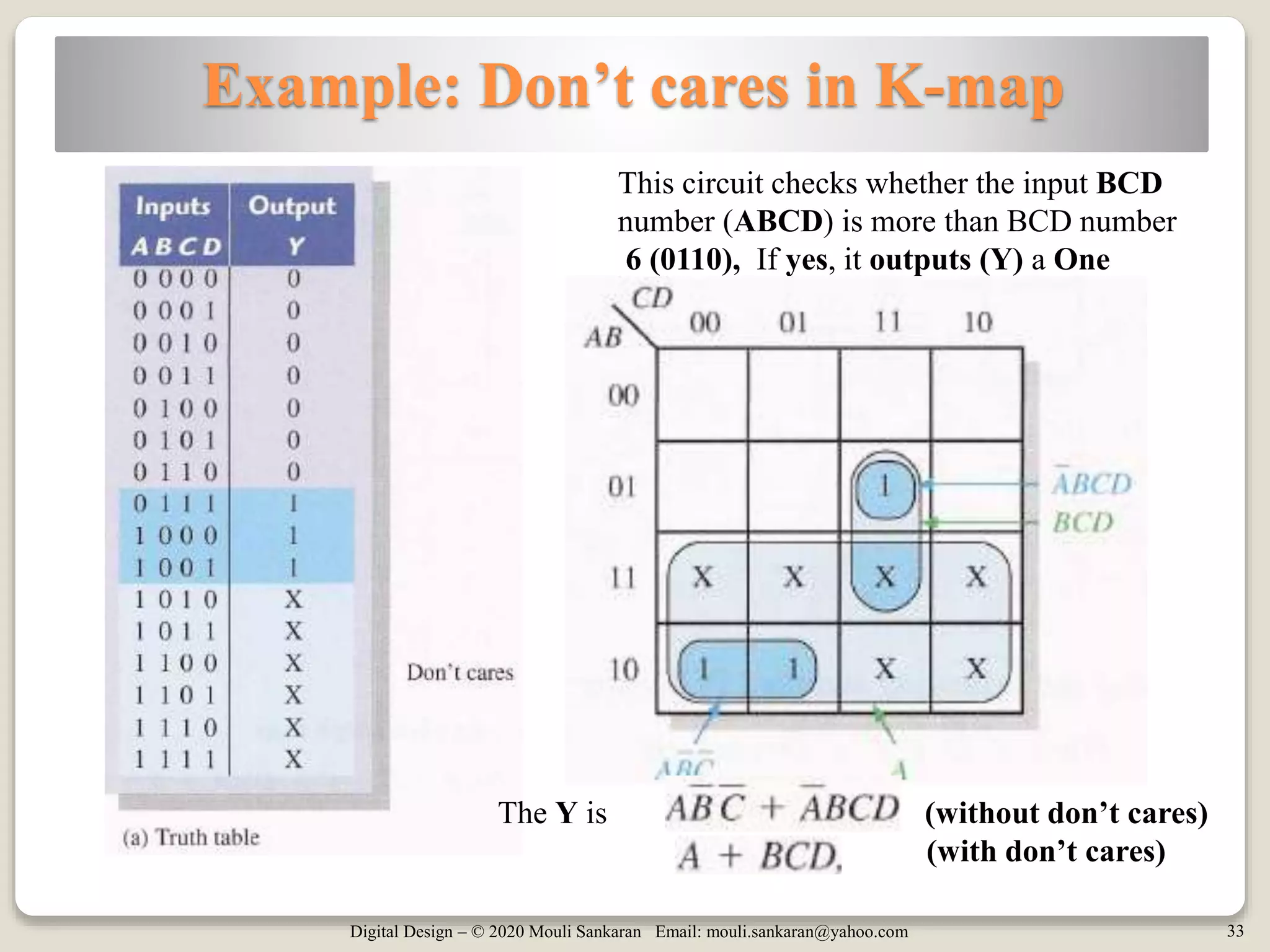
The document provides an introduction to Karnaugh maps (K-maps) used in boolean algebra for simplifying expressions. It covers the history, application, and methodology behind K-maps, including examples for Sum of Products (SOP) and Product of Sums (POS) forms, as well as the concept of 'don't care' conditions. Additionally, it discusses the implementation of 5-variable K-maps and techniques to take advantage of pattern recognition in simplification.

1. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com

2. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 2
Session 10: Focus
 Introduction to Karnaugh map
 Examples
◦ SOP form
◦ POS form
◦ Both SOP and POS
◦ Implementation
◦ 5-variable K-map
 Don’t cares in K-map
◦ Example

3. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com
Karnaugh map
Simplification Method

4. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com
Maurice Karnaugh
4
Maurice Karnaugh (born October 4, 1924) is an American physicist and
mathematician known for the Karnaugh map used in Boolean algebra.

5. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 5
Karnaugh Map
 The Karnaugh map, also known as the K-map, is a method to
simplify Boolean algebra expressions.
 Maurice Karnaugh introduced it in 1953
 It reduces the need for extensive calculations by taking
advantage of humans' pattern recognition capability
 The required Boolean results are transferred from a truth
table onto a two-dimensional grid
 Where the cells are ordered in Gray code, and
 Each cell position represents one combination of input
conditions
 while each cell value represents the corresponding output
value

6. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 6
Sample: Karnaugh Map
Courtasy: Wikipidea
This image actually shows
Two Karnaugh maps:
for the function f,
Using minterms
(colored rectangles)
and
for its complement f’,
using maxterms
(gray rectangles).

7. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 7
Why Gray Code in K-map?
 The variable combinations in the K-kap in the adjacent cells
differ only by one bit, by ordering them using Gray codes
 This helps in simplifying them by combing the adjacent
elements if both output one (for minterms) or zero (for
maxterms) since they differ by only one value

8. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 8
Example 1 (SOP)
Groups must be a power of 2.

9. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 9
Example 2 (SOP)

10. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 10
Example 3 (SOP)

11. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 11
Example 4 (SOP)

12. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 12
Example 5 (SOP)

13. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 13
Example 6 (SOP)

14. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 14
Example 7 (SOP)

15. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 15
Example 8 (SOP)

16. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 16
Example 9 (SOP)

17. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 17
SOP and POS Forms
Combing 0 terms yields:
Complement of F’ is F
POS
SOP

18. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 18
Example 1 (POS)

19. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 19
Example 2 (POS)

20. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 20
Example 3 (POS)

21. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 21
Example 4 (POS)

22. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 22
Quiz 1
Simplify the Boolean expression using K-map

23. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 23
Quiz 1: Solution

24. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 24
Quiz 2:
Simplify the Product-Of-Sums Boolean expression below,
providing a result in SOP form

25. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 25
Quiz 2: Solution
Simplify the Product-Of-Sums Boolean expression below,
providing a result in SOP form

26. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 26
Example: Both SOP and POS

27. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 27
Implementation

28. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com
5-variable K-map

29. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 29
5-variable K-Map
 5-variable (ABCDE) K-map can be built with two 4 variable
K-maps

30. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 30
Cell Adjacencies in 5-variable K-Map
 Assume two 4-variable maps are one over the other

31. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com
Don’t Cares in K-map

32. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 32
Don’t Care Conditions in K-Map
 Sometimes a situation arises in which some input variable
combinations are not allowed.
 For example, in a BCD code converter, the inputs 1010, 1011,
1100, 1101, 1110 and 1111 are all invalid
 Since these unallowed states will never occur in an application
involving the BCD code, they can be treated as “don’t care”
terms with respect to their effect on the output
 That is, for these “don’t care” terms either a 1 or a 0 may be
assigned to the output, it really does not matter since they will
never occur

33. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 33
Example: Don’t cares in K-map
This circuit checks whether the input BCD
number (ABCD) is more than BCD number
6 (0110), If yes, it outputs (Y) a One
The Y is (without don’t cares)
(with don’t cares)

34. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 34
Session 10: Summary
 Introduction to Karnaugh map
 Examples
◦ SOP form
◦ POS form
◦ Both SOP and POS
◦ Implementation
◦ 5-variable K-map
 Don’t cares in K-map
◦ Example

35. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 35
References
Ref 1 Ref 2