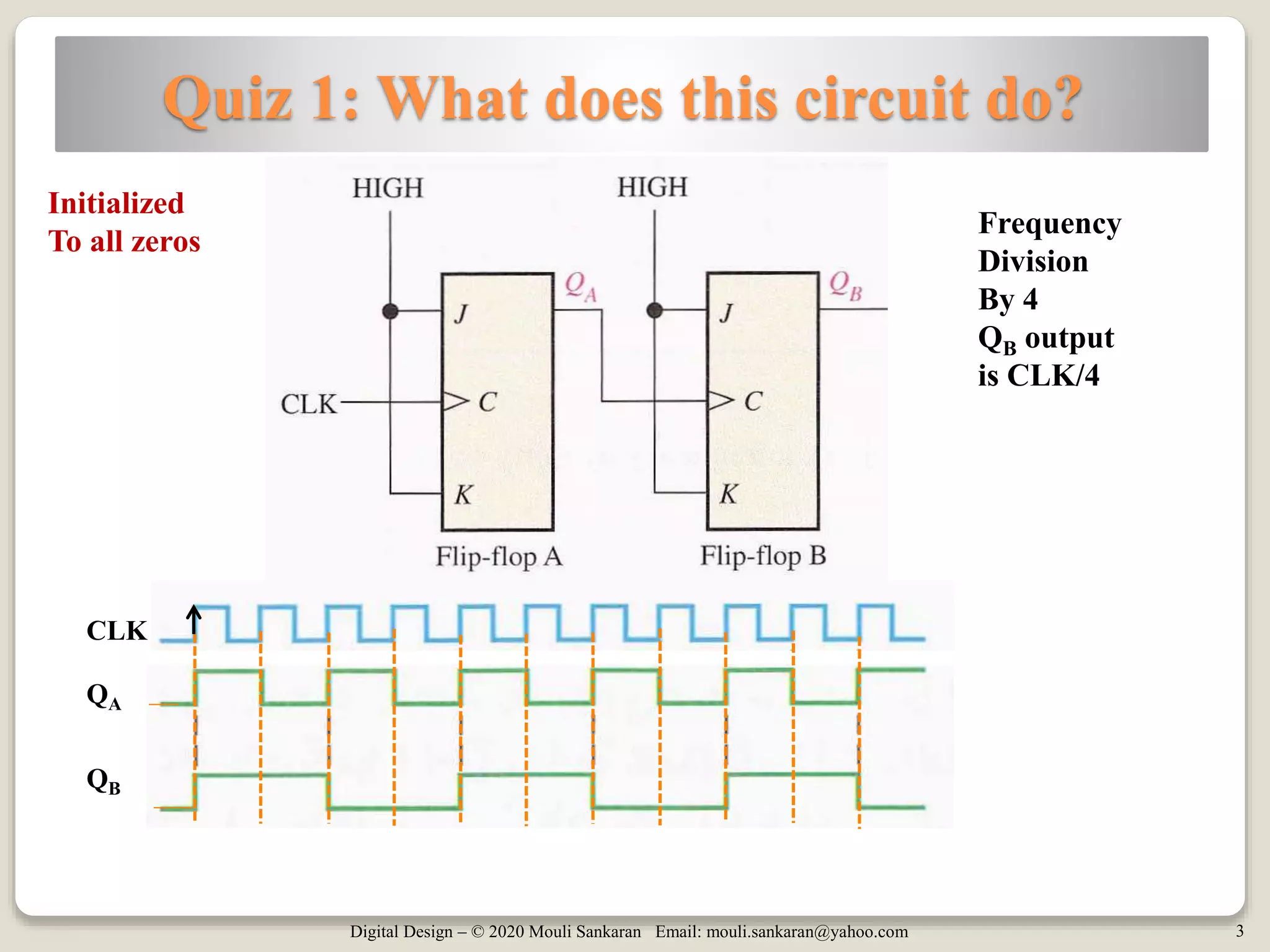
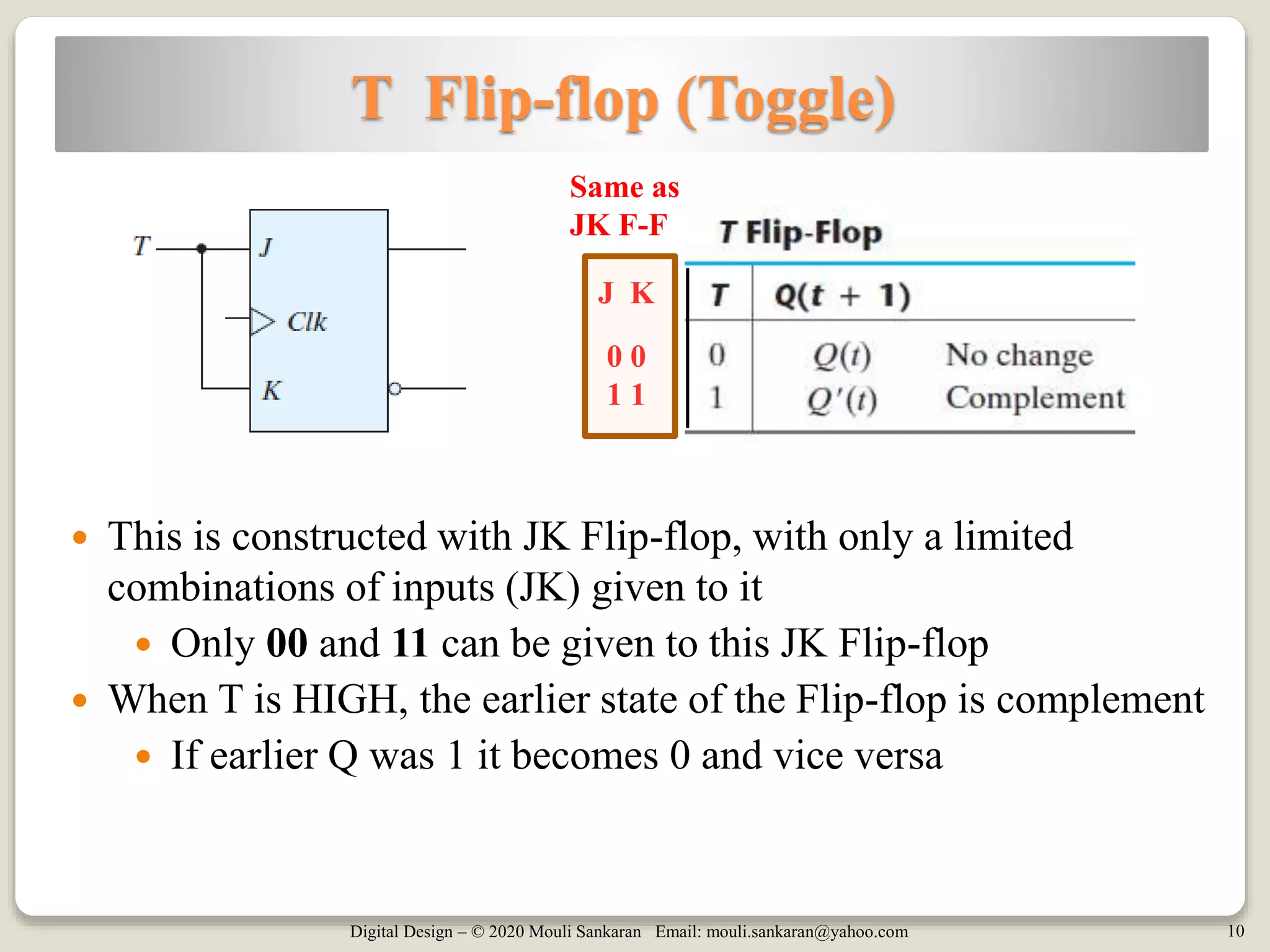
This document discusses various digital logic circuits that use JK flip-flops, including a frequency divider that divides the clock by 4, an n-bit ripple counter that counts from 0 to 2n-1, a ripple counter with a modulus less than 2n, and a 4-bit register. It also describes a T flip-flop, which is constructed from a JK flip-flop and toggles its output each time the input is pulsed high. Examples of different types of counters are provided and their operations explained.

1. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com

2. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 2
Session 23: Focus
 More Applications using JK Flip-flops
◦ Frequency Divider - Divide by 4
◦ n-bit Ripple Counter (Mod-2n Counter)
◦ Ripple Counter with Modulus less than 2n
◦ 4-bit Register
 T Flip-flop

3. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 3
Quiz 1: What does this circuit do?
Frequency
Division
By 4
QB output
is CLK/4
CLK
QA
QB
Initialized
To all zeros

4. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 4
Mod-4 or 2-bit Counter
 This a 2-bit counter that counts from 002 to 112 in binary, that
is 0 to 3 in decimal
 It has a modulus value of 4 (22) (00 → 01 → 10 → 11 , return
back to 00 ) - counts from 0 to (4-1)
 So would therefore be called a modulo-4, or mod-4, counter.
 Note also that it has taken 4 clock pulses to get from 00 to 11.
All initialized
to one (Q)
So, Q’ = 0
(which are outputs)
QB QA
MSB LSB
0 0
0 1
1 0
1 1

5. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 5
Example 1: n-bit Ripple Counter
 What edge triggered JK flip-flops?
 Is it synchronous or asynchronous?
 Do all flip-flops change state simultaneously?
 When will all outputs be stable after an input Clock
edge?
Asynchronous or serial
or ripple counter
Negative edge triggered
Initially all flip-flops are reset or cleared to zero
No
After a delay of
(n*propagation delay of flip-flop)

6. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 6
Mod-2n Counter
 Modulus counters, or simply MOD counters, are defined
based on the number of states that the counter will sequence
through before returning back to its original value.
 This n-bit ripple counter counts from 0 to (2n – 1) in binary,
which has a modulus value of 2n (2n states from 0 before
returning back to all zeros ) so would therefore be called a
modulo-2n, or mod- 2n counter.
 Note also that it has taken 2n clock pulses to get from all
zeros to all 1s

7. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 7
Example 2: Binary Ripple Counter
With a modulus of less than 2n
Counts from 0000 to 0110
It skips 0111 to 1111
due to the NAND
gate output becoming
low, when the counter
reaches 0111
Thus, Mod 7 counter

8. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 8
4-bit Register
C inputs
Changed
The clock
Input signal
To C inputs
Output of this
OR gate is
Fed as C inputs
To all D FFs

9. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com
T Flip-flop

10. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 10
T Flip-flop (Toggle)
 This is constructed with JK Flip-flop, with only a limited
combinations of inputs (JK) given to it
 Only 00 and 11 can be given to this JK Flip-flop
 When T is HIGH, the earlier state of the Flip-flop is complement
 If earlier Q was 1 it becomes 0 and vice versa
J K
0 0
1 1
Same as
JK F-F

11. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 11
Session 23: Summary
 Applications using JK Flip-flops
◦ Frequency Divider - Divide by 4
◦ n-bit Ripple Counter (Mod-2n Counter)
◦ Ripple Counter with Modulus less than 2N
◦ 4-bit Register
 T Flip-flop

12. Digital Design – © 2020 Mouli Sankaran Email: mouli.sankaran@yahoo.com 12
References
Ref 1 Ref 2