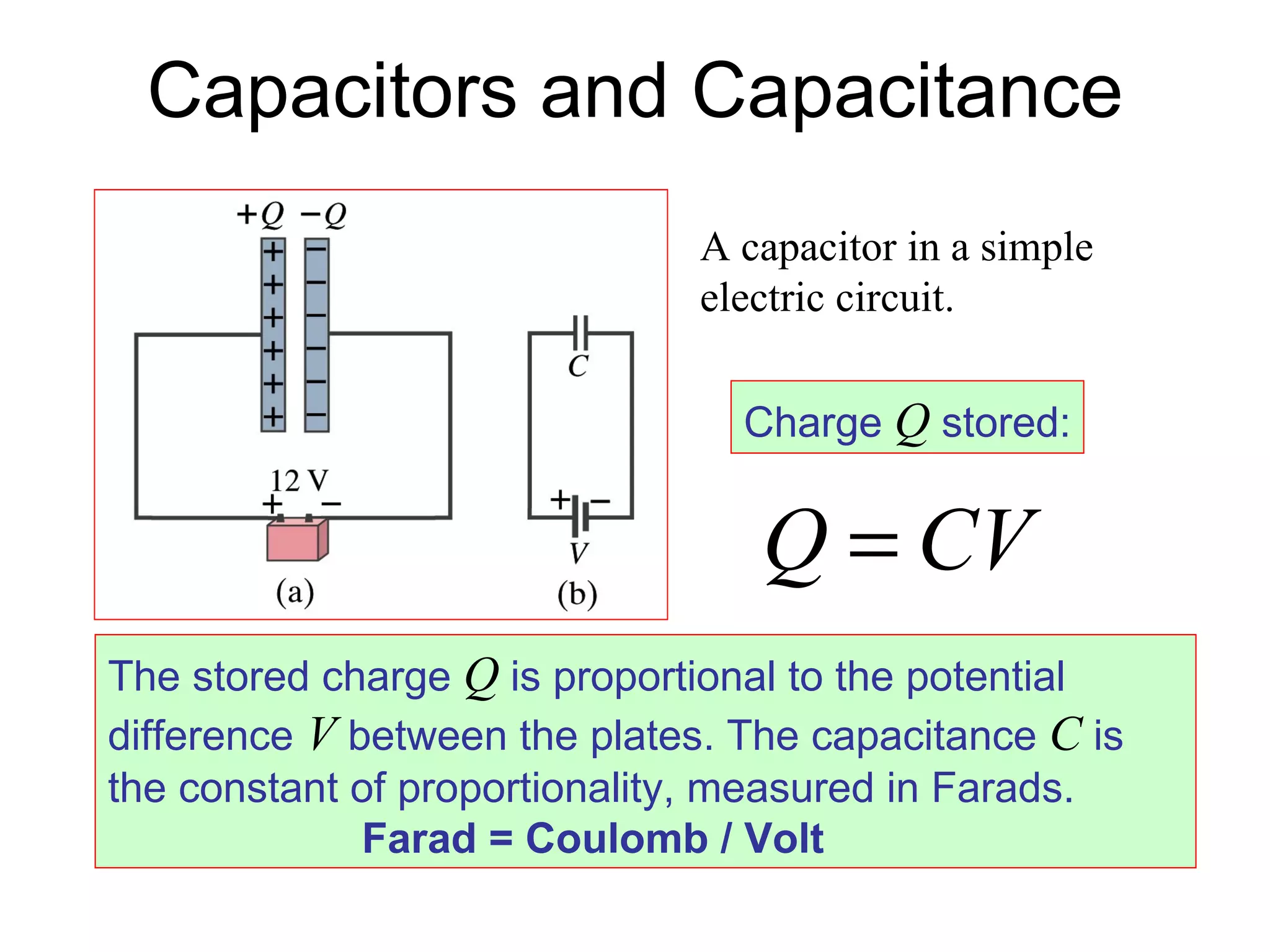
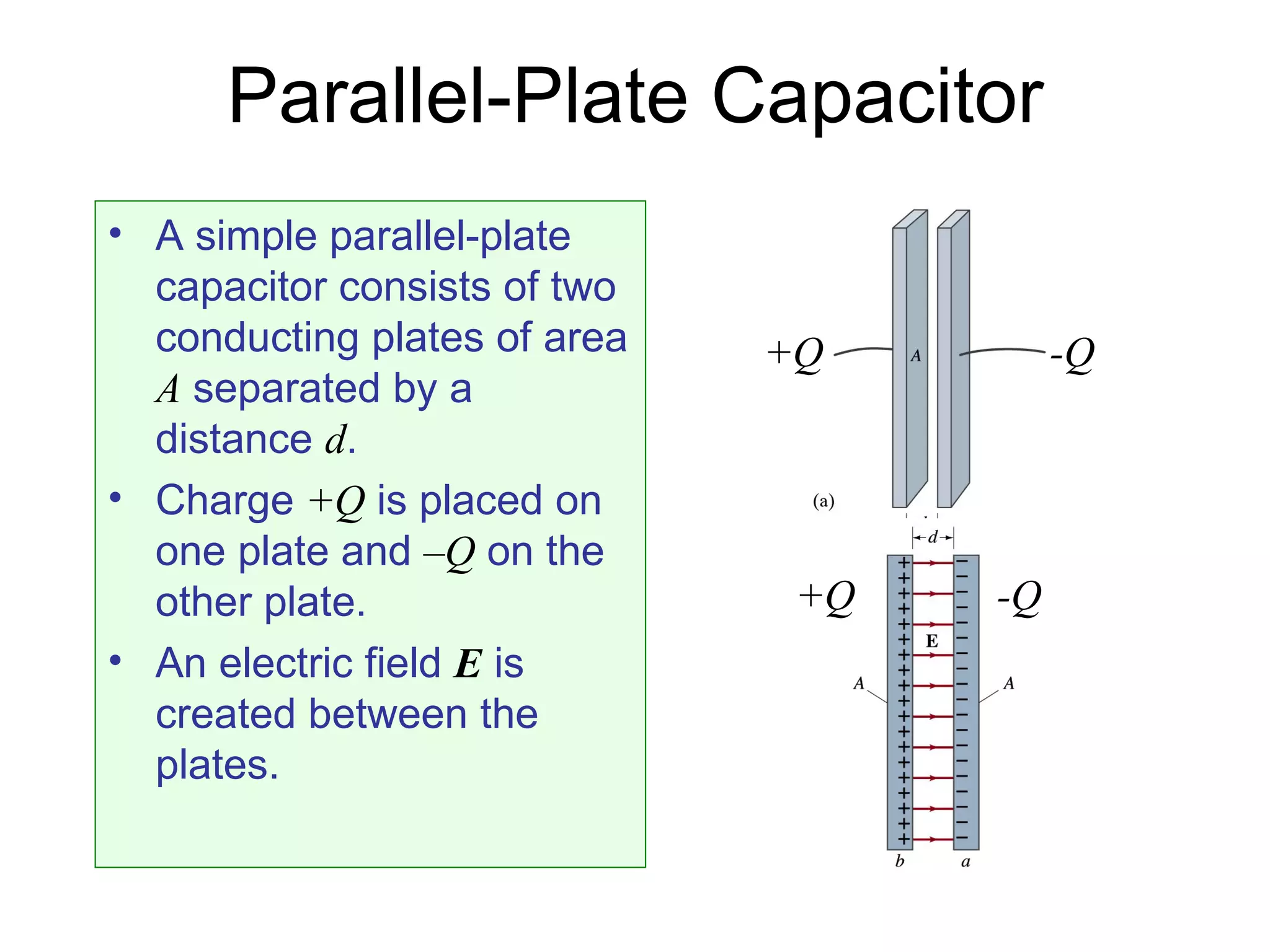
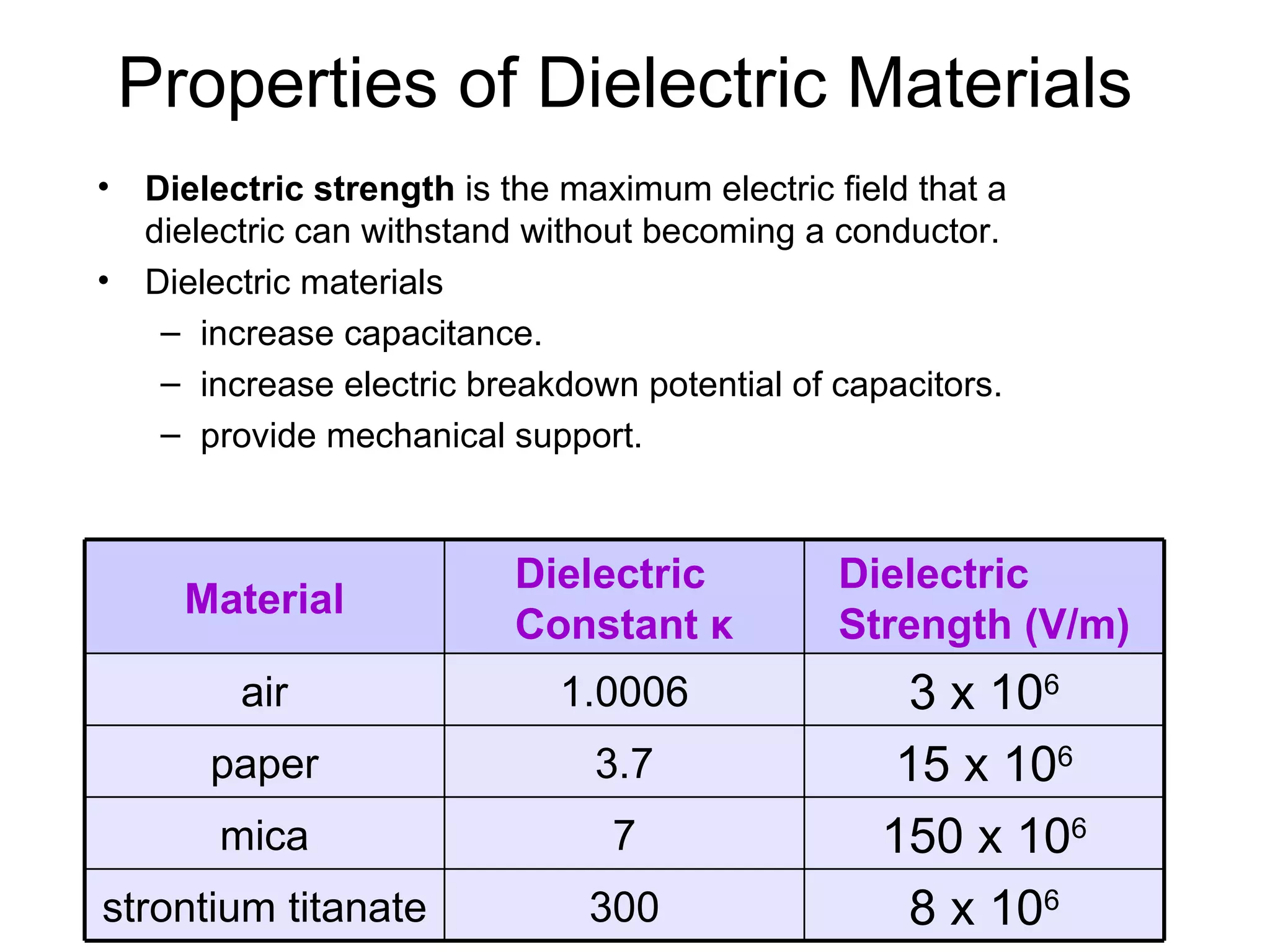
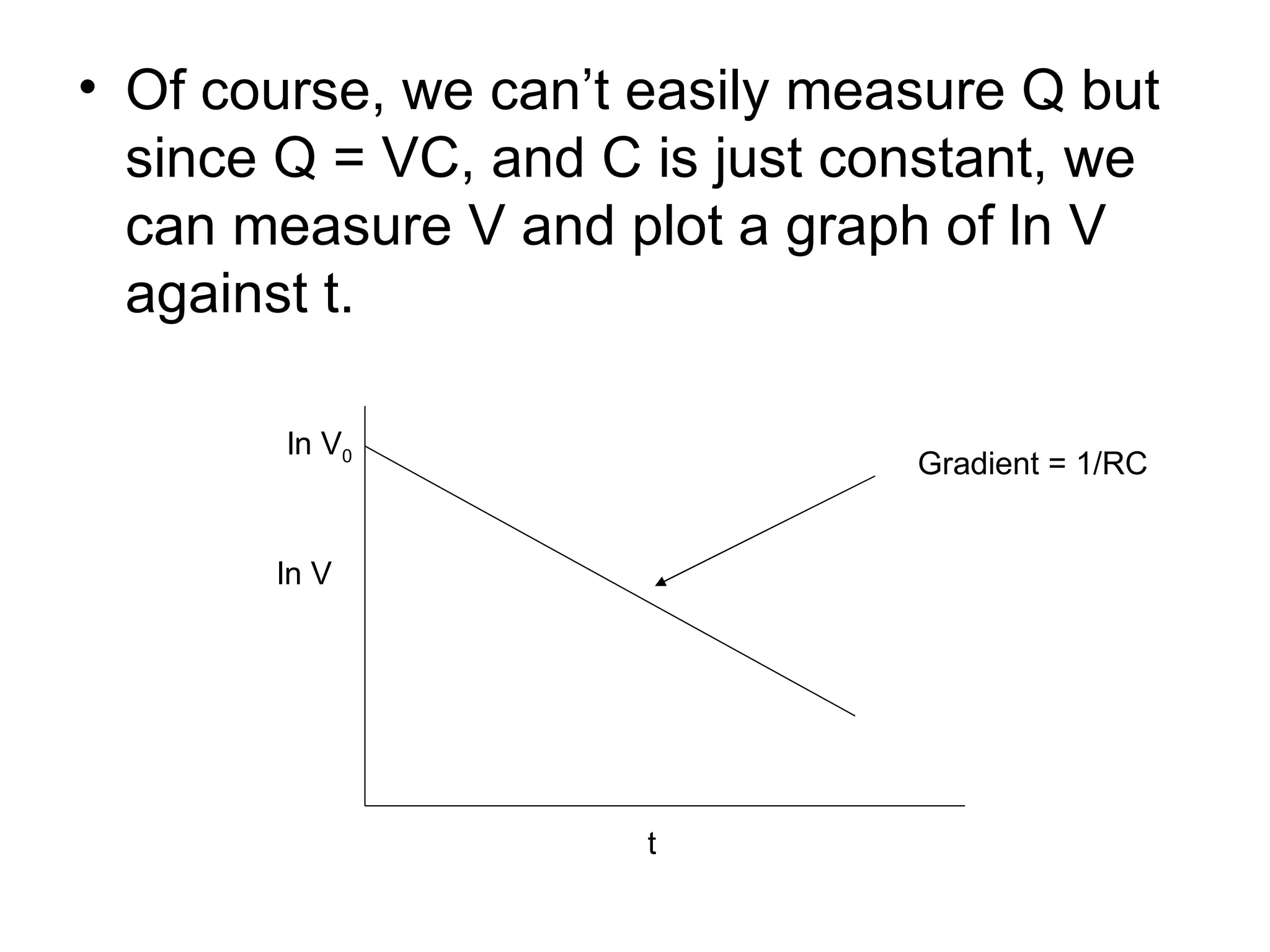
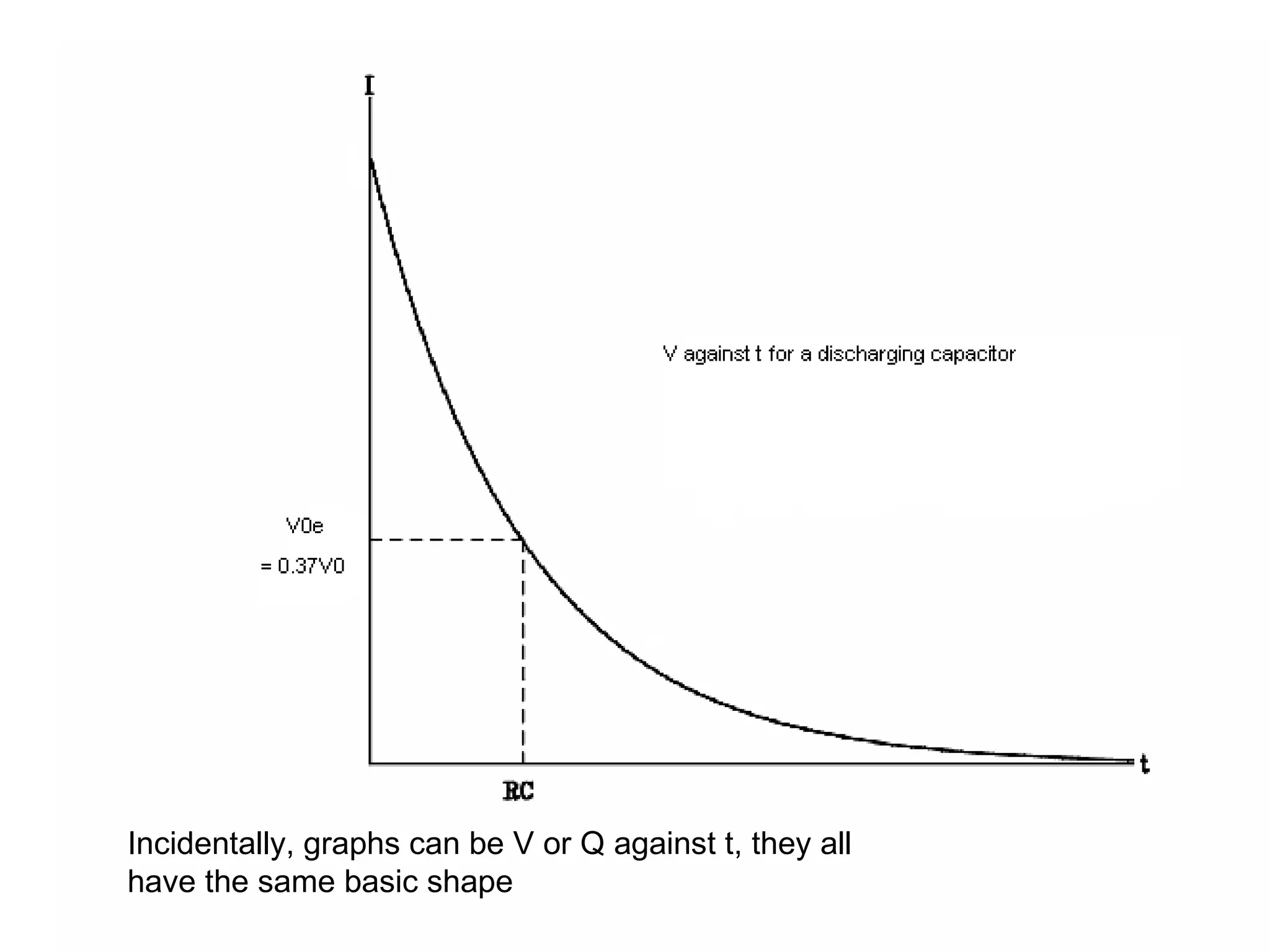
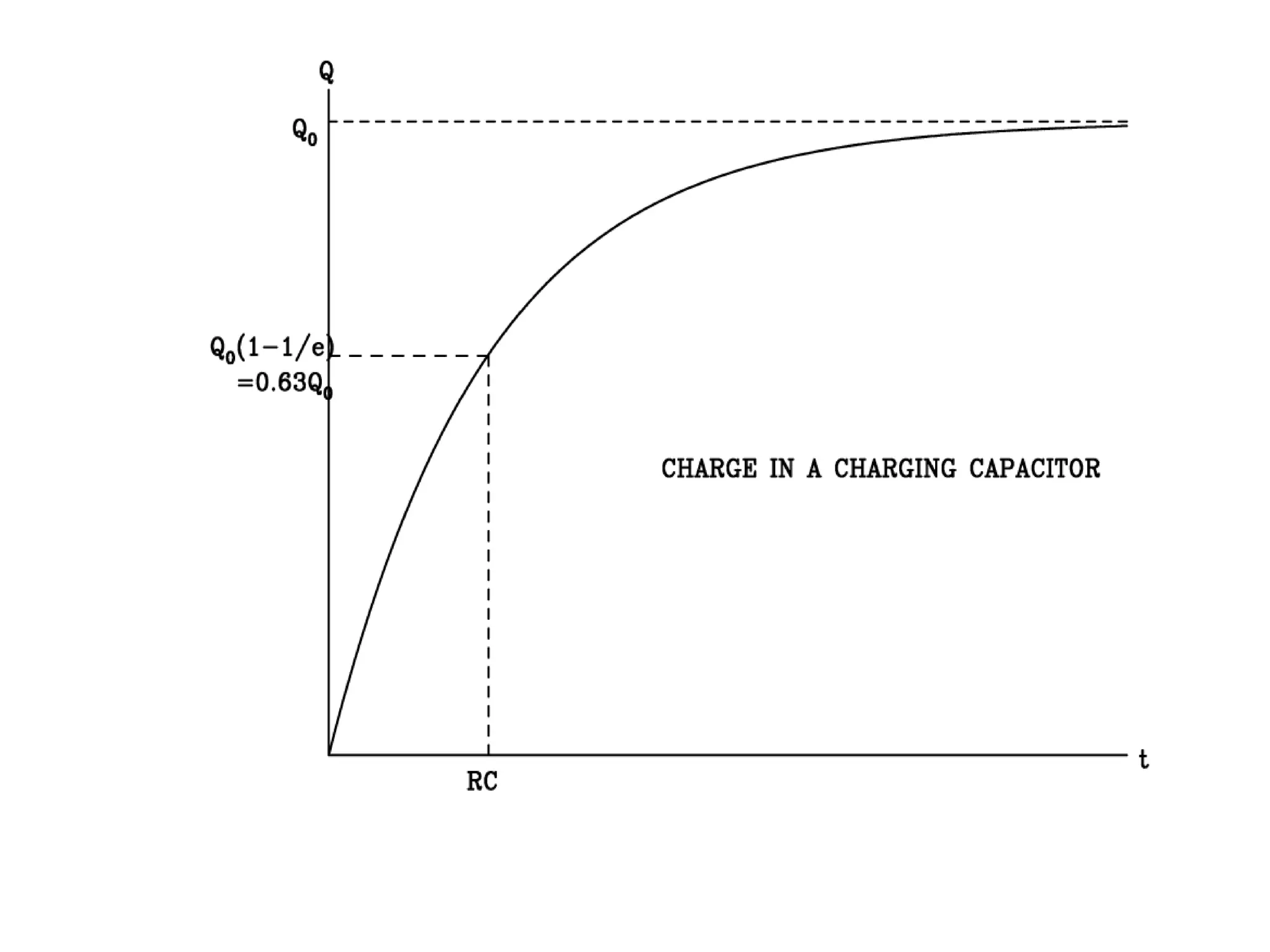
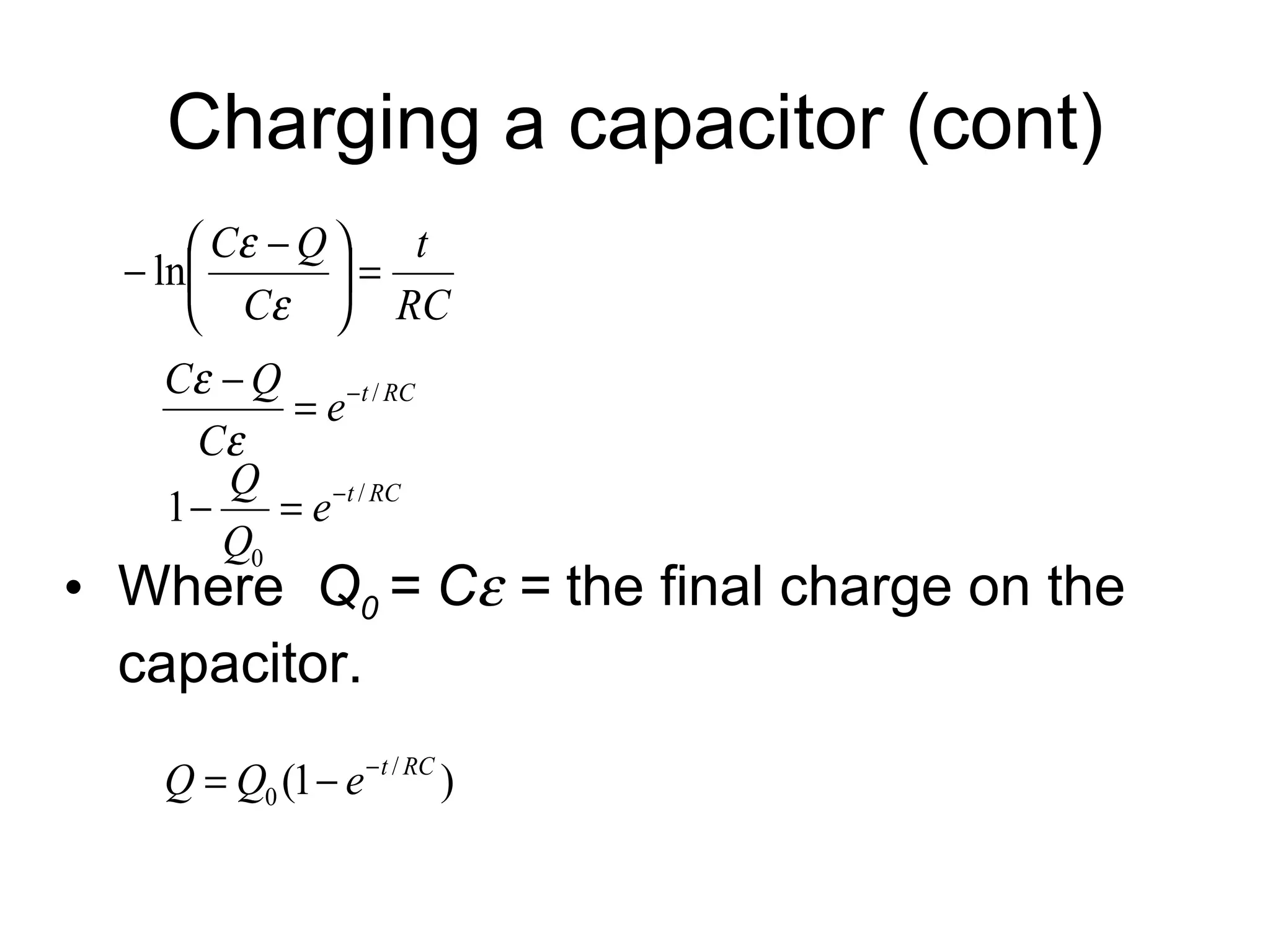A capacitor stores electric charge by having two conductors separated by an insulator. Common applications include computer memory, camera flashes, and surge protectors. The amount of charge stored is proportional to the potential difference between the plates. When a dielectric is placed between the plates, it increases the capacitance by a factor called the dielectric constant. Energy is stored in a capacitor as 1/2 CV^2 and is released when the capacitor discharges through a circuit.

1. Capacitors A capacitor is a device that stores electric charge. A capacitor consists of two conductors separated by an insulator. Capacitors have many applications: Computer RAM memory and keyboards. Electronic flashes for cameras. Electric power surge protectors. Radios and electronic circuits.

2. Types of Capacitors Parallel-Plate Capacitor Cylindrical Capacitor A cylindrical capacitor is a parallel-plate capacitor that has been rolled up with an insulating layer between the plates.

3. Capacitors and Capacitance Charge Q stored: The stored charge Q is proportional to the potential difference V between the plates. The capacitance C is the constant of proportionality, measured in Farads. Farad = Coulomb / Volt A capacitor in a simple electric circuit.

4. Parallel-Plate Capacitor A simple parallel-plate capacitor consists of two conducting plates of area A separated by a distance d . Charge +Q is placed on one plate and –Q on the other plate. An electric field E is created between the plates. +Q -Q +Q -Q

5. Energy Storage in Capacitors Since capacitors store electric charge, they store electric potential energy. Consider a capacitor with capacitance C , potential difference V and charge q . The work dW required to transfer an elemental charge dq to the capacitor: The work required to charge the capacitor from q=0 to q=Q : Energy Stored by a Capacitor = ½CV 2 = ½QV

6. Example: Electronic Flash for a Camera A digital camera charges a 100 μF capacitor to 250 V. How much electrical energy is stored in the capacitor? If the stored charge is delivered to a krypton flash bulb in 10 milliseconds, what is the power output of the flash bulb?

7. Dielectrics A dielectric is an insulating material (e.g. paper, plastic, glass) . A dielectric placed between the conductors of a capacitor increases its capacitance by a factor κ , called the dielectric constant . C= κC o ( C o =capacitance without dielectric) For a parallel-plate capacitor: ε = κε o = permittivity of the material.

8. Properties of Dielectric Materials Dielectric strength is the maximum electric field that a dielectric can withstand without becoming a conductor. Dielectric materials increase capacitance. increase electric breakdown potential of capacitors. provide mechanical support. Dielectric Strength (V/m) Dielectric Constant κ Material 3 x 10 6 1.0006 air 8 x 10 6 300 strontium titanate 150 x 10 6 7 mica 15 x 10 6 3.7 paper

9. Practice Quiz A charge Q is initially placed on a parallel-plate capacitor with an air gap between the electrodes, then the capacitor is electrically isolated. A sheet of paper is then inserted between the capacitor plates. What happens to: the capacitance? the charge on the capacitor? the potential difference between the plates? the energy stored in the capacitor?

10. Discharging a Capacitor Initially, the rate of discharge is high because the potential difference across the plates is large. As the potential difference falls, so too does the current flowing Think pressure As water level falls, rate of flow decreases

11. At some time t, with charge Q on the capacitor, the current that flows in an interval  t is: I =  Q/  t And I = V/R But since V=Q/C, we can say that I = Q/RC So the discharge current is proportional to the charge still on the plates.

12. For a changing current, the drop in charge,  Q is given by:  Q = -I  t (minus because charge Iarge at t = 0 and falls as t increases) So  Q = -Q  t/RC (because I = Q/RC) Or -  Q/Q =  t/RC

13. If we make the change infinitesimally small we get…

14. Applying the laws of logs

15. Of course, we can’t easily measure Q but since Q = VC, and C is just constant, we can measure V and plot a graph of ln V against t. ln V t Gradient = 1/RC ln V 0

16. Alternatively, if you want to get rid of the ln, just multiply both sides by e. ln Q = ln Q 0 –t/RC Becomes Q = Q 0 e -t/RC And gives a graph that looks like this…

17. Incidentally, graphs can be V or Q against t, they all have the same basic shape

18. The time constant. The time constant  =RC . The units are seconds ( t/RC is dimensionless). The time taken for the charge to fall to (1/e) of the initial value in the circuit. The time taken for the voltage to fall by ( 1/e) of its initial value.

19. Charging a capacitor At time t=0 the switch is closed, with the capacitor initially uncharged. A current will flow  =V c +V R =I 0 R , as initially V c =0. Thus the initial current is I 0 =  /R . Now a charge begins to build on the capacitor, introducing a reverse voltage. The current falls, and stops when the P.D. across C is  . Final charge is given by " Q=CV " => Q 0 =C  .

20. Charging a capacitor (quantitative). Apply Kirchoff's loop rule.

21. Charging a capacitor (cont) Where Q 0 = C  = the final charge on the capacitor.

22. Charging a capacitor (cont). To find the current, differentiate since I=dQ/dt . By considering time zero, when the current is I 0 ,

24. Energy Considerations. During charging, a total charge Q=C  flows through the battery. The battery does work W=Q 0  =C  2 . The energy stored in the capacitor is ½ QV= ½ Q 0  = ½ C  2 . Where's the other half?

25. Finally… Electromagnetism depends a lot on integrals, vectors etc. shows how useful they are. It is one of the foundations of physics but: it can be rather formal, encouraging the precise thinking that we expect of any academic training; it is rather far removed from the everyday, but that develops the imagination we expect from a physicist.