Downloaded 595 times
Uploaded byEko Supriyadi
Bab 2 fungsi
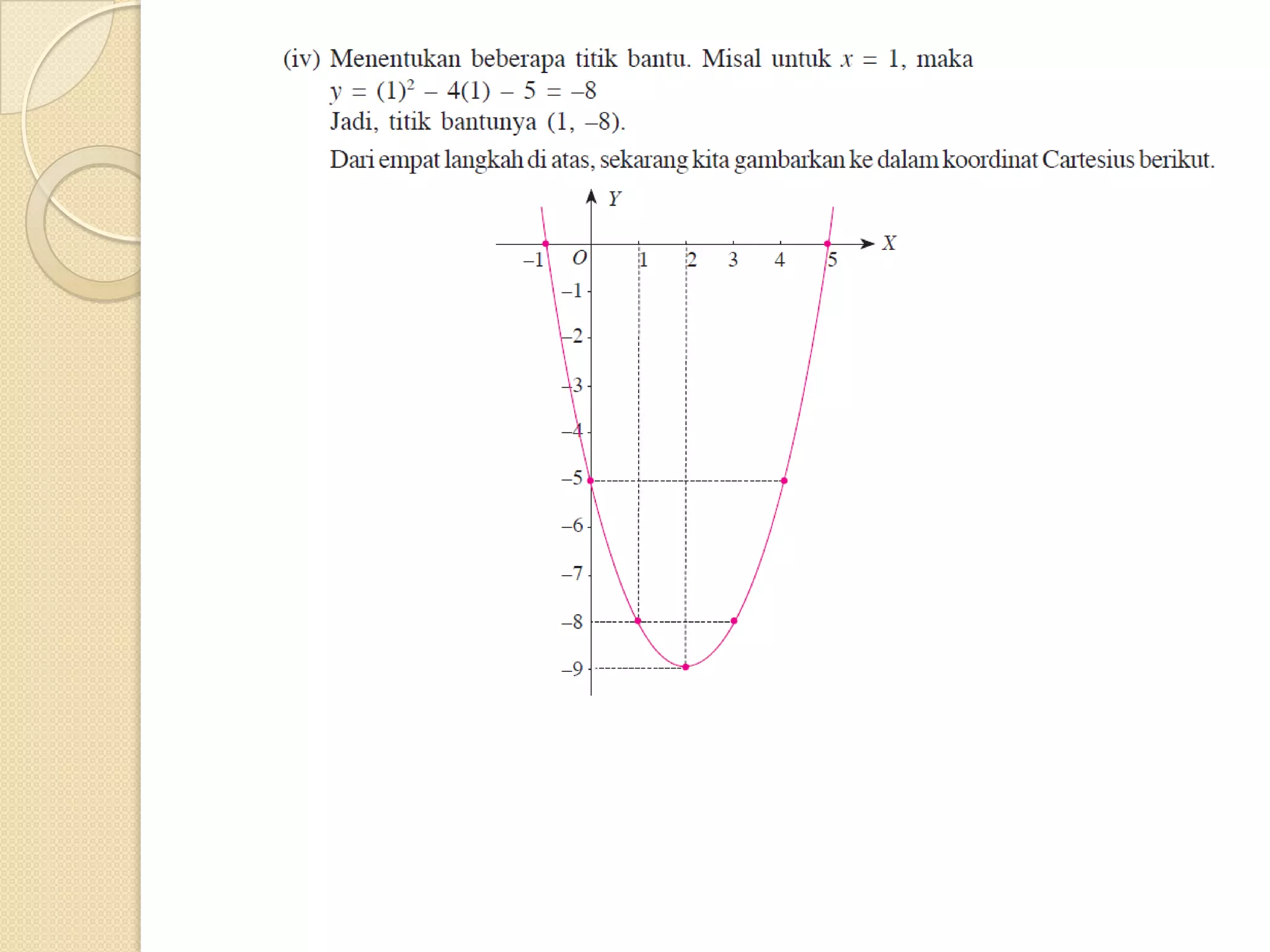
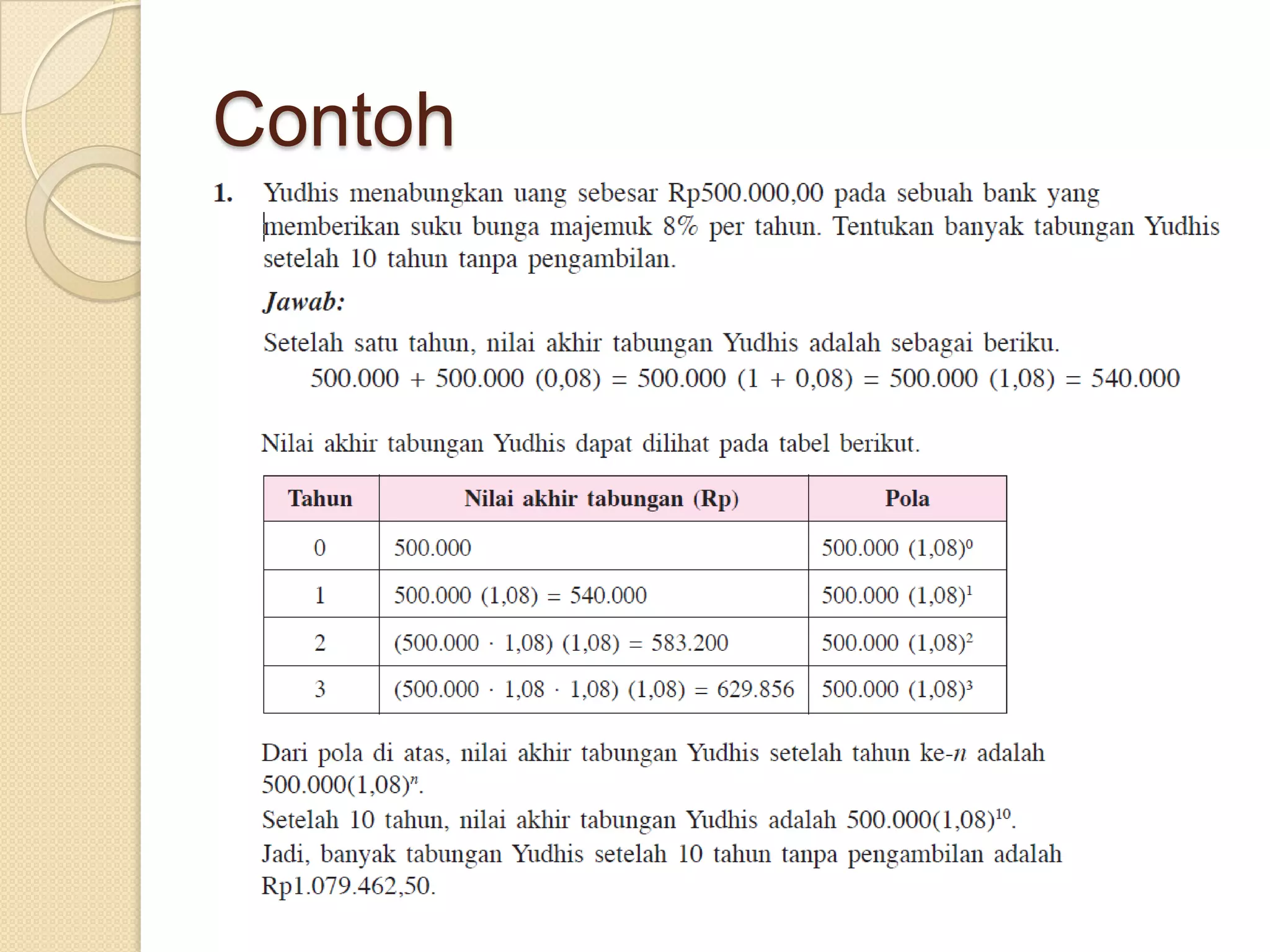
Dokumen ini membahas berbagai konsep matematika terkait fungsi, termasuk relasi, fungsi linear, fungsi kuadrat, fungsi eksponen, fungsi logaritma, dan fungsi trigonometri. Setiap jenis fungsi dijelaskan dengan definisi, grafik, dan aplikasi dalam kehidupan sehari-hari. Selain itu, terdapat penjelasan mengenai hubungan antara garis dan gradien dalam grafik fungsi linear.
More Related Content
Bab 2 fungsi
- 1.
- 2. Kompetensi Dasar • Mendeskripsikanperbedaan konsep relasi dan fungsi. • Menerapkan konsep fungsi linear. • Menggambar fungsi kuadrat. • Menerapkan konsep fungsi kuadrat. • Menerapkan konsep fungsi eksponen. • Menerapkan konsep fungsi logaritma. • Menerapkan konsep fungsi trigonometri.
- 3. A. Relasi danFungsi 1. Relasi Relasi dari himpunan A ke himpunan B adalah suatu aturan atau hubungan yang memasangkan anggota-anggota himpinan A ke anggota-anggota himpunan B. Relasi antara dua himpunan dapat dinyatakan dengan tiga cara, yaitu: a. diagram panah, b. himpunan pasangan berurutan, c. diagram Cartesius.
- 4.
- 5. 2.Fungsi Fungsi atau pemetaandari himpunan A ke himpunan B adalah suatu relasi khusus yang memasangkan setiap anggota A dengan tepat satu anggota B.
- 6.
- 7. B. Fungsi Linear 1.Bentuk Umum Fungsi Linear Fungsi linear memiliki variabel dengan pangkat tertinggi satu. Fungsi ini memetakan setiap x ∈ R ke suatu bentuk ax + b, dengan a ≠ 0, a dan b konstanta. Jika digambarkan, grafik fungsi linearakan berupa garis lurus. Himpunan titik-titik yang didapat dari fungsi f(x) = ax + b membentuk grafik yang disebut grafik fungsi linear. Grafiknya berbentuk garis lurus dengan persamaan y = mx + c, di mana m disebut gradien garis atau kemiringan garis dan c merupakan suatu konstanta.
- 8. 2. Grafik Fungsi Linear Untuk menggambar garis pada bidang Cartesius dengan persamaan y = mx + c dapat dilakukan dengan menentukan paling sedikit dua titik yang memenuhi persamaan tersebut. Selanjutnyadari kedua titik tersebut dihubungkan menjadi sebuah garis.
- 9.
- 10. 3. Gradien Persamaan Garis Lurus
- 11. 4. Menentukan Persamaan Garis Lurus ◦ Persamaan Garis Melalui Sebuah Titik (x1, y1) dan Gradien m ◦ Persamaan Garis Melalui Dua Titik (x1, y1) dan (x2, y2) Cara 1 Cara 2
- 12. ◦ Persamaan garisMelalui Titik Potong Sumbu X dan Sumbu Y
- 13.
- 14. 5. Kedudukan Dua Garis Lurus Terdapat tiga kemungkinan kedudukan antara dua garis lurus yang digambar dalam diagram Cartesius, yaitu: berpotongan, sejajar, dan berpotongan tegak lurus. a. Dua Garis Saling Berpotongan Dua garis lurus misal garis k dan garis l saling berpotongan apabila kedua gradien garis tersebut tidak sama, yaitu Titik potong dari dua garis lurus dapat ditentukan dengan cara eliminasi ataupun substitusi.
- 15. b. Dua GarisSaling Sejajar Kedudukan dua garis lurus saling sejajar (//) apabila terdapathubungan antara dua gradiennya, yaitu: dengan m1 adalah gradien garis pertama dan m2 adalah gradien garis kedua. c.Dua Garis Saling Tegak Lurus Kedudukan dua garis lurus akan saling tegak lurus (⊥) apabila hubungan antara dua gradiennya adalah sebagai berikut :
- 16.
- 17. C. Fungsi Kuadrat 1. Bentuk umum fungsi kuadrat
- 18. 2.Sifat-sifat grafik fungsikuadrat Berdasarkan nilai D a. D > 0 maka grafik memotong sumbu X di dua titik. b. D = 0 maka grafik menyinggung sumbu X. c. D < 0 maka grafik tidak memotong dan tidak menyinggung sumbu X.
- 19. Berdasarkan nilai a Jika a > 0, parabola terbuka ke atas Jika a < 0, parabola terbuka ke bawah
- 20. 3. Menggambar Grafik Fungsi Kuadrat
- 21.
- 23. 4. Penerapan Fungsi Kuadrat Fungsi kuadrat merupakan salah satu materi yang banyak dipakai dalam matematika maupun dalam mata pelajaran lain,seperti fisika, ekonomi dan juga dalam kehidupan sehari-hari. Dalam penerapan di kehidupan sehari-hari, nilai maksimum maupun minimum suatu fungsi kuadrat memegang peranan yang penting.
- 24.
- 25. D. Fungsi Eksponen 1. Bentuk umum fungsi eksponen dengan a bilangan real, a > 0 dan a ≠ 1.
- 26. Fungsi eksponen umumnyadigunakan untuk menyatakan pertumbuhan atau peluruhan yang kadar perubahannya tidak konstan. Banyak hal dalam kehidupan sehari-hari yang pertumbuhan atau peluruhannya berubah secara tidak konstan tetapi tergantung pada jumlah materi dan waktu. Beberapa contoh di antaranyaadalah a. nilai akhir suatu modal yang disimpan di bank, b. pertumbuhan organisme populasi penduduk, c. peluruhan (waktu paruh) radioaktif, d. perubahan suhu e. kecepatan reaksi kimia.
- 27.
- 28. E. Fungsi Logaritma Bentuk umum fungsi logaritma untuk a > 1, a ∈ R. Grafik fungsi eksponen y = ax dan fungsi logaritma, y = alog x
- 29.
- 30. F. Fungsi Trigonometri Bentuk-bentuk umum fungsi trigonometri Grafik f(x)= sin x
- 31.