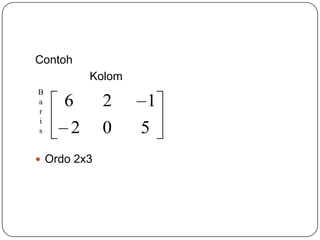
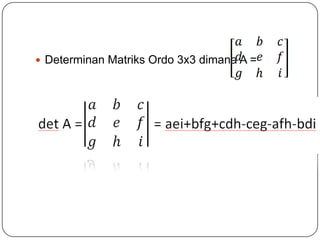
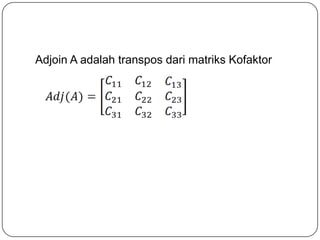
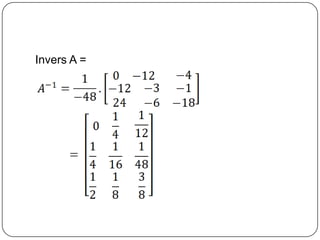
Matriks adalah susunan berbentuk persegi panjang dari elemen-elemen yang diatur berdasarkan baris dan kolom. Bab ini membahas pengertian matriks, operasi matriks seperti penjumlahan, pengurangan, dan perkalian matriks, serta konsep determinan dan invers matriks. Sistem persamaan linier dapat didefinisikan menggunakan notasi matriks.