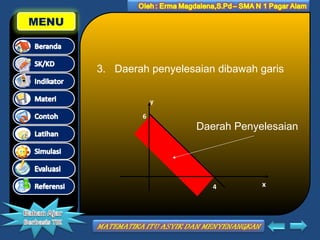
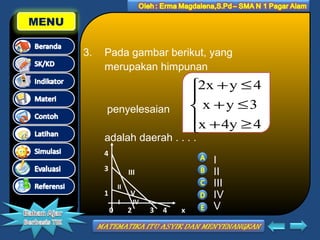
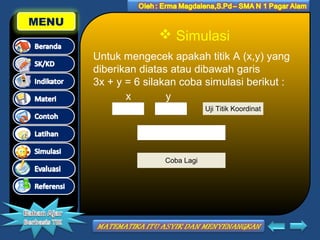
Dokumen ini membahas tentang program linear pada kelas XII IPA, termasuk standar kompetensi, kompetensi dasar, dan indikator pemelajaran. Materi yang ditawarkan meliputi cara menentukan daerah penyelesaian untuk sistem pertidaksamaan linear dua variabel, serta cara merumuskan model matematika dari masalah program linear. Terdapat juga contoh latihan untuk memperkuat pemahaman siswa mengenai topik tersebut.

1. MENU
PROGRAM LINEAR
Kelas XII IPA
Semester 1

2. MENU
Standar Kompetensi/Kompetensi Dasar
 Standar Kompetensi
Menyelesaikan masalah program linear
 Kompetensi Dasar
1 Menyelesaikan sistem
pertidaksamaan linear dua variabel
2 Merancang model matematika dari
masalah program linear

3. MENU
 Indikator
1. Menentukan penyelesaian sistem
pertidaksamaan linear dua variabel
2. Menentukan fungsi objektif dan
kendala dari program linier
3. Merumuskan model matematika
dari masalah program linear
4. Menentukan nilai optimum dari
fungsi objektif
5. Menafsirkan solusi dari masalah

4. MENU
 Materi
A. Menentukan Daerah Penyelesaian
Daerah penyelesaian pertidaksamaan
linear dua variabel dapat ditentukan
dengan langkah-langkah sebagai
berikut :
1. Menggambar garis
Titik potong Sb. x, y = 0 → ( x , 0 )
Titik potong Sb. y, x = 0 → ( 0 , y )
2. Memilih salah salah satu titik uji
diatas atau dibawah garis
3. Menentukan daerah Penyelesaian

5. MENU
B. Menentukan Pertidaksamaan
Jika diketahui gambar daerah
penyelesaian, maka pertidak- samaannya
dapat ditentukan sbb :
1. Menentukan persamaan garis
Untuk titik potong sumbu ( b, 0 )
dan ( 0, a ) memenuhi
ax + by = a.b
2. Uji salah satu daerah penyelesaian
3. Menentukan pertidaksamaannya

6. MENU
 Contoh
Contoh 1 :
Tentukan Daerah Penyelesaian 3x + 2y ≤ 12
Penyelesaian :
1. Pers Garis 3x + 2y = 12
Titik potong Sb. x, y = 0 → ( 4, 0 )
Titik potong Sb. Y, x = 0 → ( 0, 6 )
2. Titik Uji ( 0, 0 )
3 . 0 + 2 . 0 < 12

7. MENU
3. Daerah penyelesaian dibawah garis
y
6
Daerah Penyelesaian
4
x

8. MENU
Contoh 2 :
Tentukan pertidaksamaan yang
memenuhi daerah penyelesaian
pada gambar berikut :
2
( 4, 0 )
3
x

9. MENU
Penyelesaian :
1. Titik potong ( 3, 0 ) dan ( 0, 2 )
2x + 3y = 2.3
2. Titik uji ( 4, 0 ) → 2.4 + 3.0 =8 > 6
3. Pertidaksamaannya : 2x + 3y ≥ 6

10. MENU
 Latihan
1. Perhatikan gambar !
Daerah yang merupakan himpunan
penyelesaian pertidaksamaan
5x + 3y ≤ 15, x + 3y ≥ 6, x dan y ≥ 0
adalah ….
OABC
OCD
D
5
BCE
DBE
A
ABD
2
O
B
3
E
C
6
x

11. MENU
2. Daerah diarsir merupakan himpunan
penyelesaian dari pertidaksamaan ….
y
6
4
O
2
4
6
8
x
x – y ≥ 0,y – 2x ≤ 4,3x + 2y ≤ 12, x dan y ≥ 0
x – y ≤ 0,y – 2x ≥ 8,3x + 2y ≤ 24, x dan y ≥ 0
x – y ≥ 0,y – 2x ≤ 4,3x + y ≤ 24, x dan y ≥ 0
x – y ≤ 0,y – 2x ≥ 4, 3x + y ≤ 24,x dan y ≥ 0
x – y ≤ 0,y + 2x ≥ 8,3x + 2y ≤ 24, x dan y ≥ 0

12. MENU
3.
Pada gambar berikut, yang
merupakan himpunan
2x + y ≤ 4

 x +y ≤3
x + 4y ≥ 4

penyelesaian
adalah daerah . . . .
4
3
III
II
1
0
I
V
2
IV
3
4
x
I
II
III
IV
V

13. MENU
Daerah diarsir pada
gambar berikut
merupakan himpunan
penyelesaian sistem
pertidaksamaan . . . .
y
12
5
0
x ≥ 0, 6x + y ≤ 12, 5x + 4y ≥ 20
x ≥ 0, 6x + y ≥ 12, 5x + 4y ≤ 20
x ≥ 0, 6x + y ≤ 12, 4x + 5y ≥ 20
x ≥ 0, x + 6y ≤ 12, 4x + 5y ≥ 20
x ≥ 0, x + 6y ≤ 12, 5x + 4y ≥ 20
2 4
x

14. MENU
 Simulasi
Untuk mengecek apakah titik A (x,y) yang
diberikan diatas atau dibawah garis
3x + y = 6 silakan coba simulasi berikut :
x
y
Uji Titik Koordinat
Coba Lagi

15. MENU
 Referensi
• Ari Damari.2007. Kupas Matematika SMA
Untuk Kels X, XI, dan XII. Jakarta : PT
Wahyu Media.
• Cecep Anwar H.F.S.2008. Matematika
Aplikasi untuk SMA dan MA Kelas XII
Program IPA. Jakarta : Pusat Perbukuan
BSE Depdiknas
• Sartono Wirodikromo.2004. Matematika
SMA Kelas XII IPA. Jakarta : PT Erlangga.
• Siswanto. 2005.Matematika Inovatif 3
Konsep dan Aplikasinya Untuk Kelas XII
SMA Program IPA. Solo : PT Tiga
Serangkai Pustaka Mandiri

16. MENU