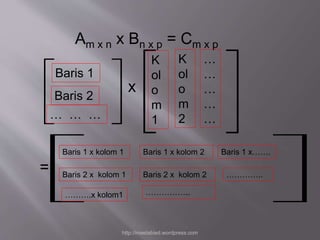
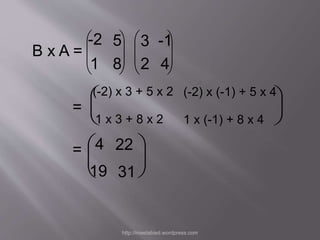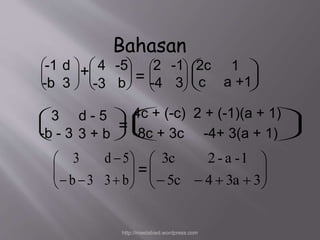Dokumen tersebut membahas tentang operasi perkalian matriks dan invers matriks beserta contoh-contoh penyelesaiannya. Dijelaskan syarat dan cara mengalikan dua buah matriks serta sifat-sifat perkalian matriks seperti tidak bersifat komutatif. Juga dijelaskan pengertian invers matriks dan cara mencari invers matriks berukuran 2x2.