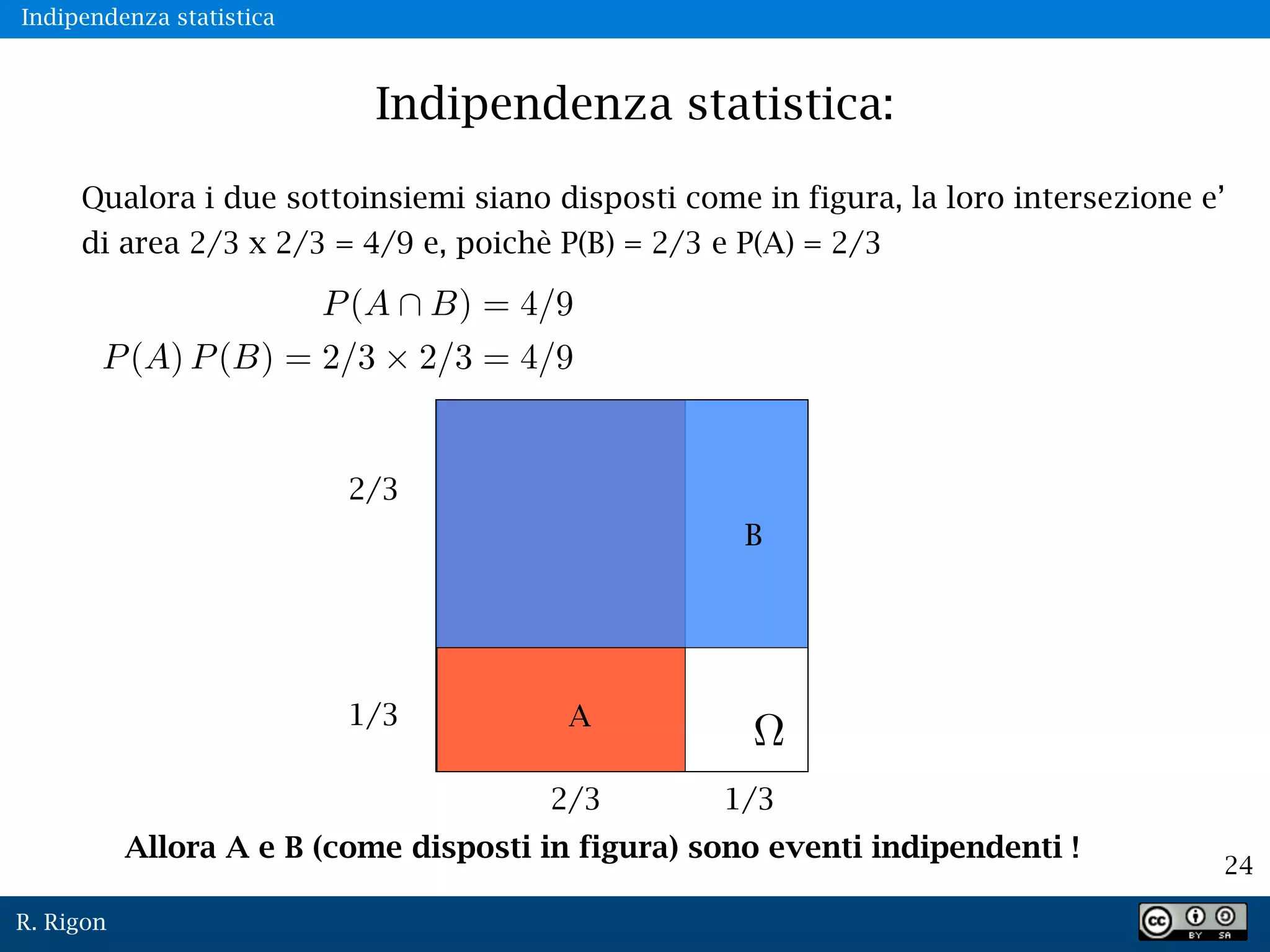
Il documento fornisce un'introduzione ai concetti fondamentali della teoria della probabilità, esplorando definizioni formali e assiomi che ne governano il calcolo. Viene discusso il concetto di probabilità condizionale e indipendenza statistica, con esempi pratici per chiarire come queste nozioni si applicano a insiemi di eventi. Infine, si enfatizza l'importanza dell'assegnazione delle probabilità come chiave per comprendere completamente i fenomeni descritti.

1. Un ripasso di probabilità:
Assiomi
PaulKlee,GiardinodiTunisi,1919
Riccardo Rigon

2. R. Rigon
2
Definizione Intuitiva ?
Intuitivamente, la probabilità potrebbe essere definita come:
Dove N(a) è il numero di eventi (favorevoli) osservati su N grandi
tentativi.
P(a) = lim
N ⇥
N(a)
N
Ma questa definizione non è priva di contraddizioni !
Assiomi e concetti di base

3. R. Rigon
3
Una definizione formale
• Sia Ω lo spazio degli eventi:
– Esso contiene tutte le possibili realizzazioni di un determinato
esperimento
– è un singolo evento
– è un insieme di eventi
– E’ richiesto che sia una sigma-algebra
A
Assiomi e concetti di base

4. R. Rigon
4
Una definizione più formale
gli assiomi della probabilità
e.g. Feller, 1968
Assiomi e concetti di base

5. R. Rigon
5
Non perseguiremo qui la prova dei seguenti enunciati. Tuttavia,
una evidenza intuitiva deriva dall’associare alla probabilità
l’area della figura geometrica disegnata nelle slides che
seguono.
Altre proprietà della probabilità.
dedotte dagli assiomi 1-3:
Assiomi e concetti di base

6. R. Rigon
6
Altre proprietà della probabilità.
dedotte dagli assiomi 1-3:
Se
A + Ac
=
Allora:
P(A) = 1 P(Ac
)
A
Ac
Assiomi e concetti di base

7. R. Rigon
7
Altre proprietà della probabilità.
dedotte dagli assiomi 1-3:
A ⇥ B =⇤ P(A) P(B)
B A
B
Assiomi e concetti di base

8. R. Rigon
8
Altre proprietà della probabilità.
dedotte dagli assiomi 1-3:
P(A ⇥ B) = P(A) + P(B) P(A ⇤ B)
A
Assiomi e concetti di base

9. R. Rigon
9
Altre proprietà della probabilità.
dedotte dagli assiomi 1-3:
P(A ⇥ B) = P(A) + P(B) P(A ⇤ B)
B
Assiomi e concetti di base

10. R. Rigon
10
Altre proprietà della probabilità.
dedotte dagli assiomi 1-3:
P(A ⇥ B) = P(A) + P(B) P(A ⇤ B)
A B
A B
Assiomi e concetti di base

11. R. Rigon
11
Un esempio di calcoli base
Si consideri, a titolo di esempio, lo spazio degli eventi contenente sette elementi,
E1 , E2, ... , E7.
E siano le probabilità definite come:
p(E1) = p(E2) = p(E3) = p(E7) = 1/5, p(E4) = p(E5) = 1/20,
e
p(E6) = 1/10.
Assiomi e concetti di base

12. R. Rigon
12
A = {E1, E2, E3, E5, E6}
p(A) = p(E1) + p(E2) + p(E3) + p(E5) + p(E6) =
(1/5) + (1/5) + (1/5) + (1/20) + (1/10) = ¾ = .75
B = {E2, E3, E4, E7}
p(B) = p(E2) + p(E3) + p(E4) + p(E7) = (1/5) + (1/5) +(1/20) +
(1/5) = 13/20 = .65
Un esempio di calcoli base
Assiomi e concetti di base

13. R. Rigon
13
Il problema centrale
non è il calcolo: che risulta “automatico”. Ma l’assegnazione
delle probabilità ovvero della forma funzionale della P( ).
Quando si conosce la probabilità, si conosce tutto del fenomeno che
si va descrivendo: se ne è assegnata “la fisica”.
Assiomi e concetti di base

14. R. Rigon
14
La probabilità condizionale
Si dice che una probabilità è condizionale, se essa è assegnata in
seguito alla conoscenza della realizzazione di uno o più eventi e si
scrive:
L a c o n o s c e n z a c h e c i h a
permesso di assegnare la
probabilità
Assiomi e concetti di base

15. R. Rigon
15
La probabilità condizionale
Si dice che una probabilità è condizionale, se essa è assegnata in
seguito alla conoscenza della realizzazione di uno o più eventi e si
scrive:
O più semplicemente:
se l’evento x è condizionato da y
Assiomi e concetti di base

16. R. Rigon
16
Probabilità composte
Come negli esempi iniziali, è possibile considerare, il contemporaneo
realizzarsi di più insiemi di eventi. Si parla allora di Probabilità
congiunta, indicata con le due scritture equivalenti:
A, B
Assiomi e concetti di base

17. R. Rigon
17
Probabilità composte
Come negli esempi iniziali, è possibile considerare, il contemporaneo
realizzarsi di più insiemi di eventi. Si parla allora di Probabilità
congiunta:
La probabilità è, in questo caso,
l’area del trapezio rosso,
rispetto all’area di
A, B
Assiomi e concetti di base

18. R. Rigon
18
Probabilità condizionali
La probabilità condizionale è invece definita come
Pertanto
Assiomi e concetti di base

19. Riccardo Rigon
!19
Dunque
La probabilità (pdf) di due eventi A e B congiunti è data da
dove P(A | B) è la probabilità di ottenere A da un campione casuale, sapendo che
B è certo, èd è chiamata probabilità condizionale di A rispetto ad B, e P(B) è la
probabilità di ottenere B. Equivalentemente il teorema si legge anche:
vista la simmetria esistente tra gli insiemi A e B
Bayes Theorem

20. Riccardo Rigon
!20
La regola di Bayes
Vale allora la Regola di Bayes
Bayes Theorem
Che di solito è scritta come:

21. R. Rigon
21
Indipendenza statistica:
A e B sono detti statisticamente indipendenti se
Analogamente, se gli Aj sono indipendenti, allora
e
Indipendenza statistica

22. R. Rigon
22
Indipendenza statistica:
Il concetto di indipendenza statistica estende quello del calcolo combinatorico
di eventi discreti, ma non è affatto intuitivo geometricamente.
Esso afferma, nella sostanza, che l’area dell’intersenzione (non nulla) di due
insiemi è uguale al prodotto delle aree degli insiemi. L’indipendenza statistica
rappresenta perciò una equazione che deve essere soddisfatta.
A
B
Indipendenza statistica

23. R. Rigon
23
Indipendenza statistica:
Sia considerato, per illustrare l’esempio, uno spazio degli eventi rappresentato
da un quadrato di lato unitario e i due suoi sottoinsiemi con un lato unitario ed
uno, lungo 2/3
A
B
Indipendenza statistica

24. R. Rigon
24
Indipendenza statistica:
Qualora i due sottoinsiemi siano disposti come in figura, la loro intersezione e’
di area 2/3 x 2/3 = 4/9 e, poichè P(B) = 2/3 e P(A) = 2/3
A
B
Allora A e B (come disposti in figura) sono eventi indipendenti !
2/3
1/3
2/3 1/3
Indipendenza statistica

25. R. Rigon
25
Indipendenza statistica:
Se i due insiemi A e B sono fatti muovere parallelamente a se stessi, in base alla
definizione data, si ottengono altri insieme isomorfi ai primi che rimangono
indipendenti.
A
B
2/3
1/3
2/3 1/3
Indipendenza statistica

26. R. Rigon
26
Indipendenza statistica:
In altre configurazioni, some quella rappresentata sotto, non sono più
indipendenti statisticamente.
A
B
2/3
1/3
2/3 1/3
Indipendenza statistica

27. R. Rigon
27
concetti di base
•La probabilità è una teoria matematica basata su alcuni assiomi
•La probabilità congiunta rappresenta è anch’essa una probabilità
•La probabilità condizionale è anch’essa una probabilità
•L’indipendenza probabilistica (o statistica) consente di semplificare il
calcolo delle probabilità congiunte
Altri
Indipendenza statistica