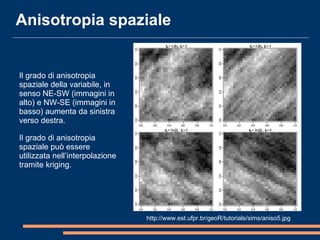
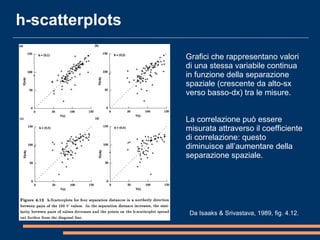
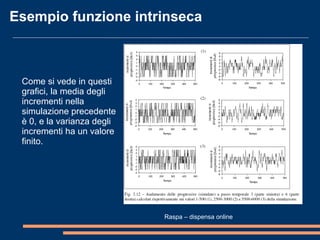
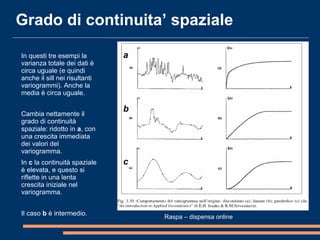
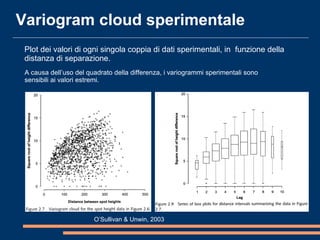
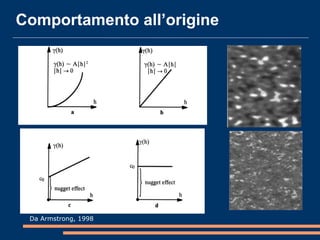
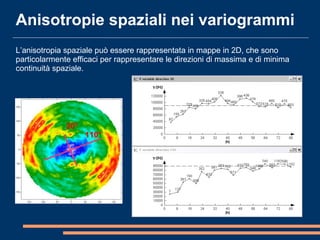
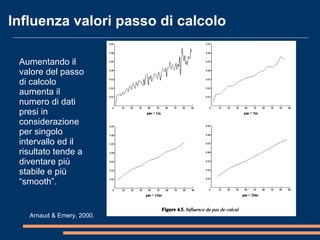
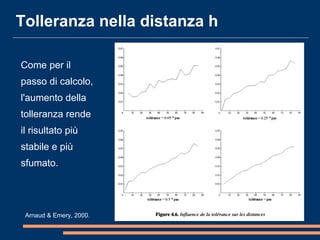
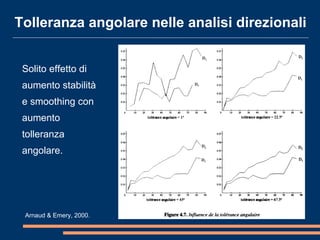
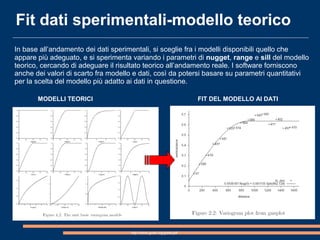
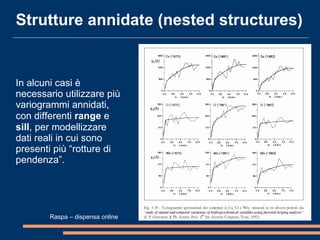
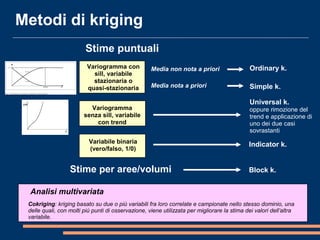
Il documento analizza la correlazione e l'anisotropia spaziale in variabili geostatistiche, mostrando come la continuità spaziale e le differenze di varianza siano influenzate dalla separazione tra le osservazioni. Vengono presentati strumenti e metodi come il variogramma e tecniche di kriging, evidenziando l'importanza di considerare le proprietà statistiche nelle analisi spaziali. Infine, si discutono modelli teorici per adattare i dati sperimentali e metodi di cokriging per migliorare le stime attraverso variabili correlate.

1. Correlazione spaziale
http://www.est.ufpr.br/geoR/tutorials/sim2D.html
Queste immagini
rappresentano simulazioni
di variabili con differenti
gradi di correlazione
spaziale, che aumenta da
sinistra verso destra e
dall’alto verso il basso. I
valori della variabile sono
proporzionali alla intensità
del grigio.
La variabile in alto a sinistra
ha una continuità spaziale
molto inferiore a quella
rappresentata nell’immagine
in basso a destra.

2. Anisotropia spaziale
Il grado di anisotropia
spaziale della variabile, in
senso NE-SW (immagini in
alto) e NW-SE (immagini in
basso) aumenta da sinistra
verso destra.
Il grado di anisotropia
spaziale può essere
utilizzata nell’interpolazione
tramite kriging.
http://www.est.ufpr.br/geoR/tutorials/sims/aniso5.jpg

3. Come misurare la correlazione spaziale?
Una variabile che presenta
correlazione spaziale avrà
valori sempre meno simili
all’aumentare della
separazione tra la coppia di
valori confrontata.
Calcolando la differenza dei
valori in funzione della
separazione spaziale tra le
due osservazioni si può
riconoscere l'influsso della
correlazione spaziale.
separazione
Raspa – dispensa online

4. Da Isaaks & Srivastava, 1989, fig. 4.12.
h-scatterplots
Grafici che rappresentano valori
di una stessa variabile continua
in funzione della separazione
spaziale (crescente da alto-sx
verso basso-dx) tra le misure.
La correlazione può essere
misurata attraverso il coefficiente
di correlazione: questo
diminuisce all’aumentare della
separazione spaziale.

5. Applicabile quando i primi due momenti statistici (media e covarianza) di una variabile
esistono ed hanno le seguenti proprietà:
Media = E(Z(x)) = E(Z(x+h)) = m (costante , indipendentemente dal punto in cui viene
misurata)
E: expected, valore atteso (medio) di una variabile.
h: separazione spaziale tra le due osservazioni.
Covarianza = Cov(Z(x+h),Z(x)) = E((Z(x)-mx
)(Z(x+h)-mx+h
)) = E(Z(x)Z(x+h)) – m2
= C(h)
La covarianza tra due osservazioni separate da una distanza h è finita e dipende solo dal
valore di h, non dalla particolare posizione.
Come stimare i valori?
Ipotesi della stazionarietà di secondo grado (second-order
stationarity o “debole”)

6. L’ipotesi stazionaria di secondo grado spesso non è
applicabile ai dati naturali di cui si dispone.
Esempio
Krige (1951) descrive un caso in cui la varianza sperimentale
in un giacimento aurifero dell’Africa del Sud cresceva
indefinitamente aumentando la dimensione del supporto
considerato sino a considerare l’intero giacimento.
Distribuzioni con varianza non definita

7. Ipotesi intrinseca
Per cercare di superare il problema delle misure non stazionarie e
con varianza indefinita, Matheron (1963, 1965) introdusse un’ipotesi
di lavoro, l’ipotesi intrinseca, che non prende direttamente in
considerazione la variabile, ma i suoi incrementi:
gli incrementi della funzione stocastica considerata sono
stazionari
E(Z(x+h)-Z(x)) = m(h) = 0
La differenza attesa tra i valori misurati in due siti separati da una distanza h è funzione
solo di h, inoltre essa sarà uguale a zero.
Var(Z(x+h)-Z(x)) = 2γ(h)
La varianza delle differenze fra osservazioni separate da una distanza h è finita e
dipende solo dal valore della distanza tra i siti, h, e non dalla posizione locale. La
funzione γ(h) è chiamata semi-variogramma.

8. Esempio funzione intrinseca
Come si vede in questi
grafici, la media degli
incrementi nella
simulazione precedente
è 0, e la varianza degli
incrementi ha un valore
finito.
Raspa – dispensa online

9. Il variogramma
Var(Z(x+h)-Z(x)) = 2γ(h)
Il variogramma è lo strumento di base per analizzare la correlazione
spaziale dei dati continui.
Alcune proprietà dei variogrammi:
γ(0) = 0
γ(h) >= 0
γ(-h) = γ(h)

10. Caratteristiche del variogramma
Sill: limite superiore del variogramma (se esiste)
Range: distanza massima di correlazione delle variabili, in corrispondenza
della quale si raggiunge il sill.
Da T5_GeostatisticAnalysis.ppt

11. Grado di continuita’ spaziale
In questi tre esempi la
varianza totale dei dati è
circa uguale (e quindi
anche il sill nei risultanti
variogrammi). Anche la
media è circa uguale.
Cambia nettamente il
grado di continuità
spaziale: ridotto in a, con
una crescita immediata
dei valori del
variogramma.
In c la continuità spaziale
è elevata, e questo si
riflette in una lenta
crescita iniziale nel
variogramma.
Il caso b è intermedio.
a
b
c
Raspa – dispensa online

12. Variogram cloud sperimentale
Plot dei valori di ogni singola coppia di dati sperimentali, in funzione della
distanza di separazione.
O’Sullivan & Unwin, 2003
A causa dell’uso del quadrato della differenza, i variogrammi sperimentali sono
sensibili ai valori estremi.

13. La semivarianza degli incrementi può essere stimata
utilizzando i dati osservati:
2
)(
1
))()((
)(2
1
)( ∑=
+−=
hn
i
ii hxzxz
hn
hγ

Il variogramma sperimentale
n(h) è il numero di osservazioni separate da una distanza h, con un
valore di tolleranza su questa, per esempio +/- 50% rispetto
all’incremento fisso, in maniera da coprire in maniera completa
l’intervallo delle distanze.

14. Il variogramma sperimentale
Il plot della semivarianza degli incrementi versus gli
incrementi è chiamato semi-variogramma sperimentale.
Raspa – dispensa online

15. Comportamento all’origine
Da Armstrong, 1998, fig. 3.3.
Da Armstrong, 1998

16. Anisotropie spaziali nei variogrammi
Da Armstrong, 1998, fig. 3.5a.
La correlazione spaziale può avere valori differenti lungo differenti
direzioni: in generale si può individuare una direzione di massima
correlazione ed una, ortogonale, di minima correlazione.

17. Anisotropie spaziali nei variogrammi
L’anisotropia spaziale può essere rappresentata in mappe in 2D, che sono
particolarmente efficaci per rappresentare le direzioni di massima e di minima
continuità spaziale.
110°
20°

18. Parametri calcolo variogramma sperimentale
Passo di calcolo – Lag
Tolleranza nella distanza h - Lag tolerance
Tolleranza angolare nelle analisi direzionali - Angular tolerance
Da Pannatier, 1996, fig. 4.8

19. Aumentando il
valore del passo
di calcolo
aumenta il
numero di dati
presi in
considerazione
per singolo
intervallo ed il
risultato tende a
diventare più
stabile e più
“smooth”.
Arnaud & Emery, 2000.
Influenza valori passo di calcolo

20. Arnaud & Emery, 2000.
Tolleranza nella distanza h
Come per il
passo di calcolo,
l'aumento della
tolleranza rende
il risultato più
stabile e più
sfumato.

21. Arnaud & Emery, 2000.
Tolleranza angolare nelle analisi direzionali
Solito effetto di
aumento stabilità
e smoothing con
aumento
tolleranza
angolare.

22. Variogrammi con sill
Pepitico
Sferico
Raspa – dispensa online

23. Variogrammi con sill
Esponenziale
Gaussiano
Raspa – dispensa online

24. Variogrammi periodici
Raspa – dispensa online

25. Fit dati sperimentali-modello teorico
In base all’andamento dei dati sperimentali, si sceglie fra i modelli disponibili quello che
appare più adeguato, e si sperimenta variando i parametri di nugget, range e sill del modello
teorico, cercando di adeguare il risultato teorico all’andamento reale. I software forniscono
anche dei valori di scarto fra modello e dati, così da potersi basare su parametri quantitativi
per la scelta del modello più adatto ai dati in questione.
MODELLI TEORICI FIT DEL MODELLO AI DATI
http://www.gstat.org/gstat.pdf

26. Strutture annidate (nested structures)
In alcuni casi è
necessario utilizzare più
variogrammi annidati,
con differenti range e
sill, per modellizzare
dati reali in cui sono
presenti più “rotture di
pendenza”.
Raspa – dispensa online

27. Metodi di kriging
Analisi multivariata
Cokriging: kriging basato su due o più variabili fra loro correlate e campionate nello stesso dominio, una
delle quali, con molti più punti di osservazione, viene utilizzata per migliorare la stima dei valori dell’altra
variabile.
Ordinary k.
Simple k.
Universal k.
oppure rimozione del
trend e applicazione di
uno dei due casi
sovrastanti
Variogramma con
sill, variabile
stazionaria o
quasi-stazionaria
Variogramma
senza sill, variabile
con trend
Variabile binaria
(vero/falso, 1/0)
Media non nota a priori
Media nota a priori
Stime puntuali
Stime per aree/volumi Block k.
Indicator k.

28. Bibliografia
G. Raspa. Capitolo 3 - Geostatistica di base
http://w3.uniroma1.it/geostatistica/Geostatistica/Dispense.pdf
Isaaks & Srivastava, 1989. An introduction to Applied Geostatistics. Oxford
Univ. Press
Armstrong, 1998. Basic Linear Geostatistics. Springer Verlag.
Arnaud & Emery, 2000. Estimation et interpolation spatiale. Hermes Science,
Paris.
Wackernagel, 1998. Multivariate Geostatistics. Springer Verlag.
Pannatier, 1996. Variowin. Software for Spatial Data Analysis in 2D.