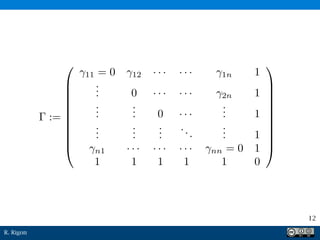
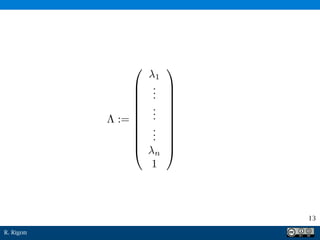
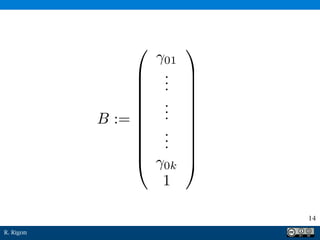
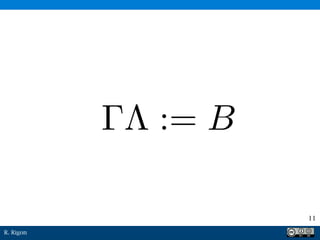Il documento discute il kriging come metodo di interpolazione lineare per stimare grandezze a partire da dati noti. Viene sottolineato l'importanza della correttezza della stima e della minimizzazione dell'errore, con il presupposto che la media sia costante. Infine, viene presentato un sistema lineare per determinare i pesi associati alle stime.

1. Riccardo Rigon
Kriging
Equations

2. R. Rigon
2
Kriging
Si assume che la stima di una certa grandezza sia ottenibile
come interpolazione lineare delle grandezze note:
Definito l’errore:

3. R. Rigon
3
Kriging
Il primo requisito di uno stimatore vorrà che in media, su
tutte le realizzazioni ovvero, la stima sia corretta (unbiased).
Nell’ultimo passaggio, si è assunto che la media esista e sia costante ovunque.
In questo caso il Kriging si chiama Simple Kriging

4. R. Rigon
4
La correttezza della stima implica dunque che la somma dei pesi sia uguale ad
1 e solo n-1 dei pesi siano indipendenti tra di loro.
Kriging

5. R. Rigon
5
La seconda richiesta è che l'errore di stima sia minimo
Kriging

6. R. Rigon
6

7. R. Rigon
7
definendo la covarianza a due punti:

8. R. Rigon
8
definendo il variogramma:
Si può scrivere:

9. R. Rigon
9
Imponendo che l’errore sia minimo, si ha:

10. R. Rigon
10
Al variare degli indici i e k la precedente equazione
costituisce un sistema lineare nei
pesi che può essere scritto in forma compatta.

11. R. Rigon
11

12. R. Rigon
12

13. R. Rigon
13

14. R. Rigon
14

15. R. Rigon
15
Thank you
Ulrici,2000?