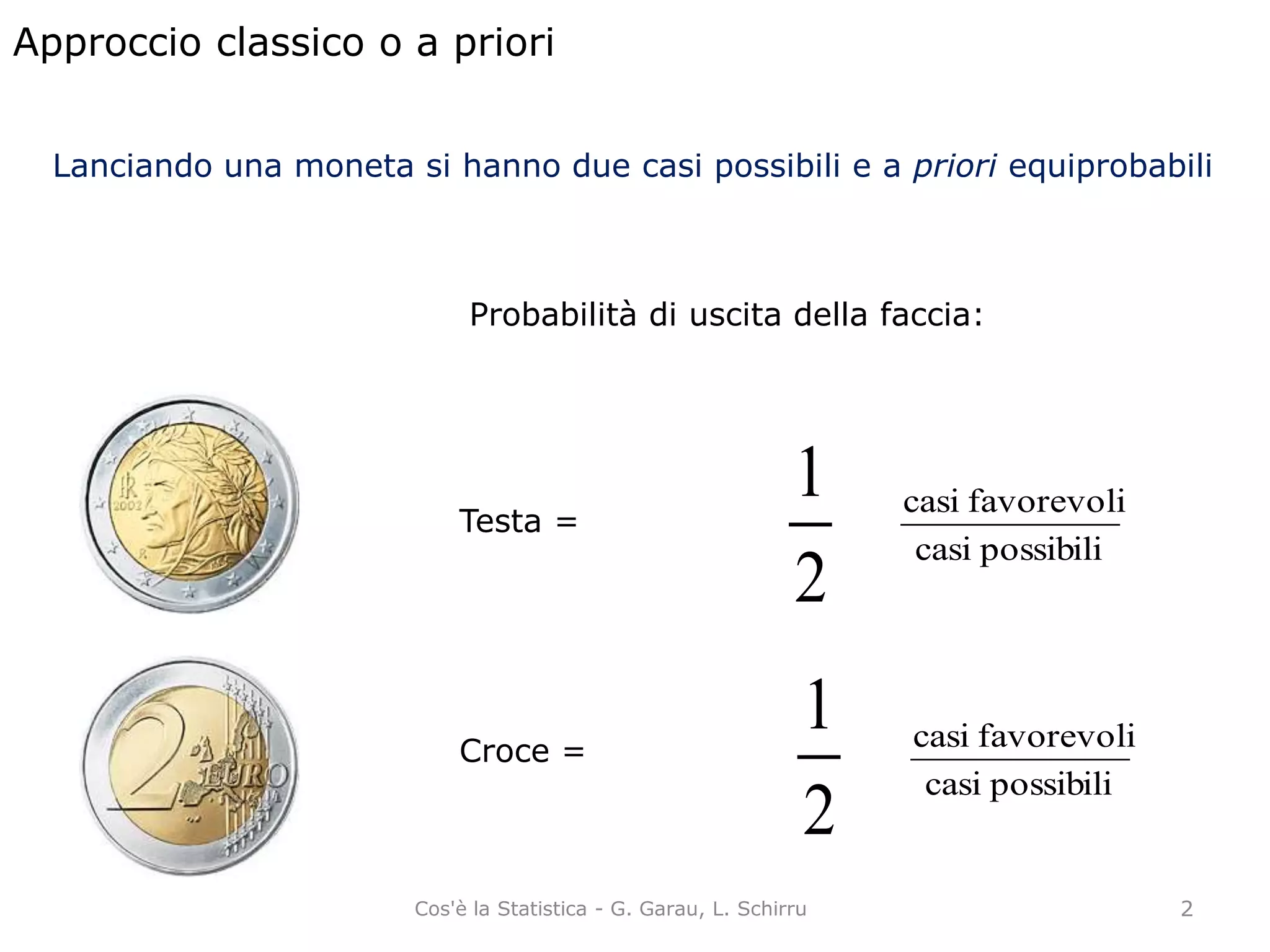
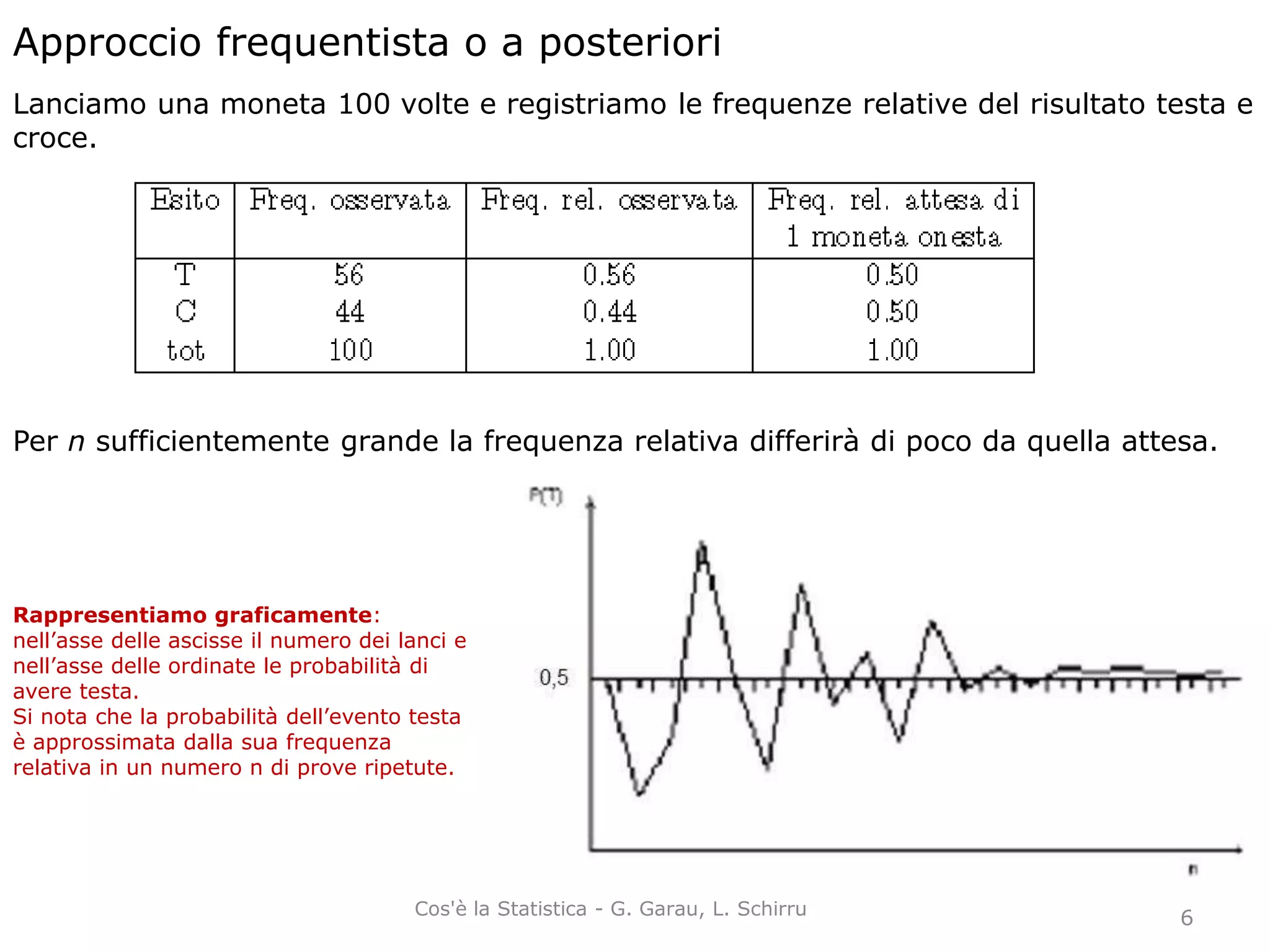
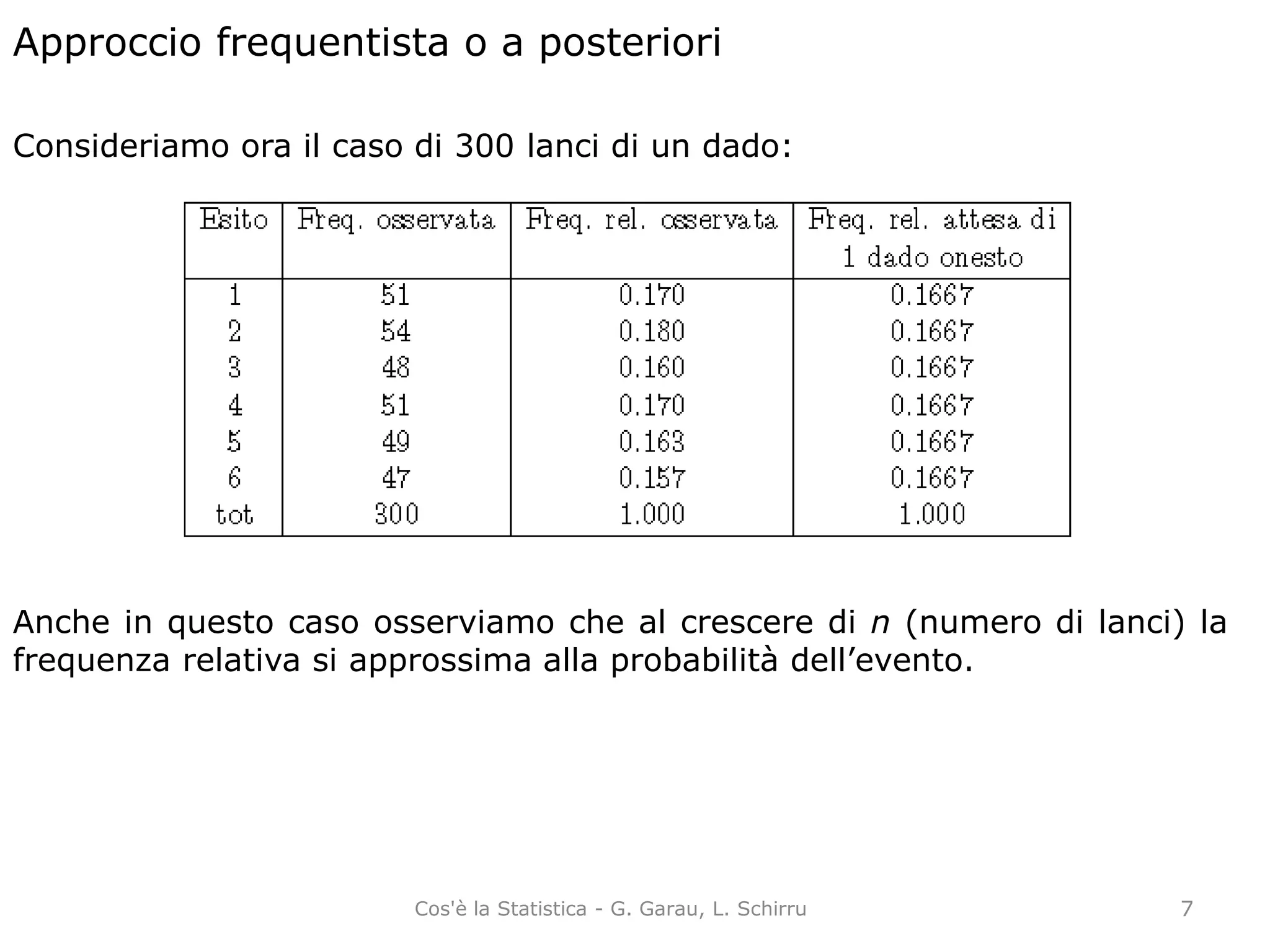
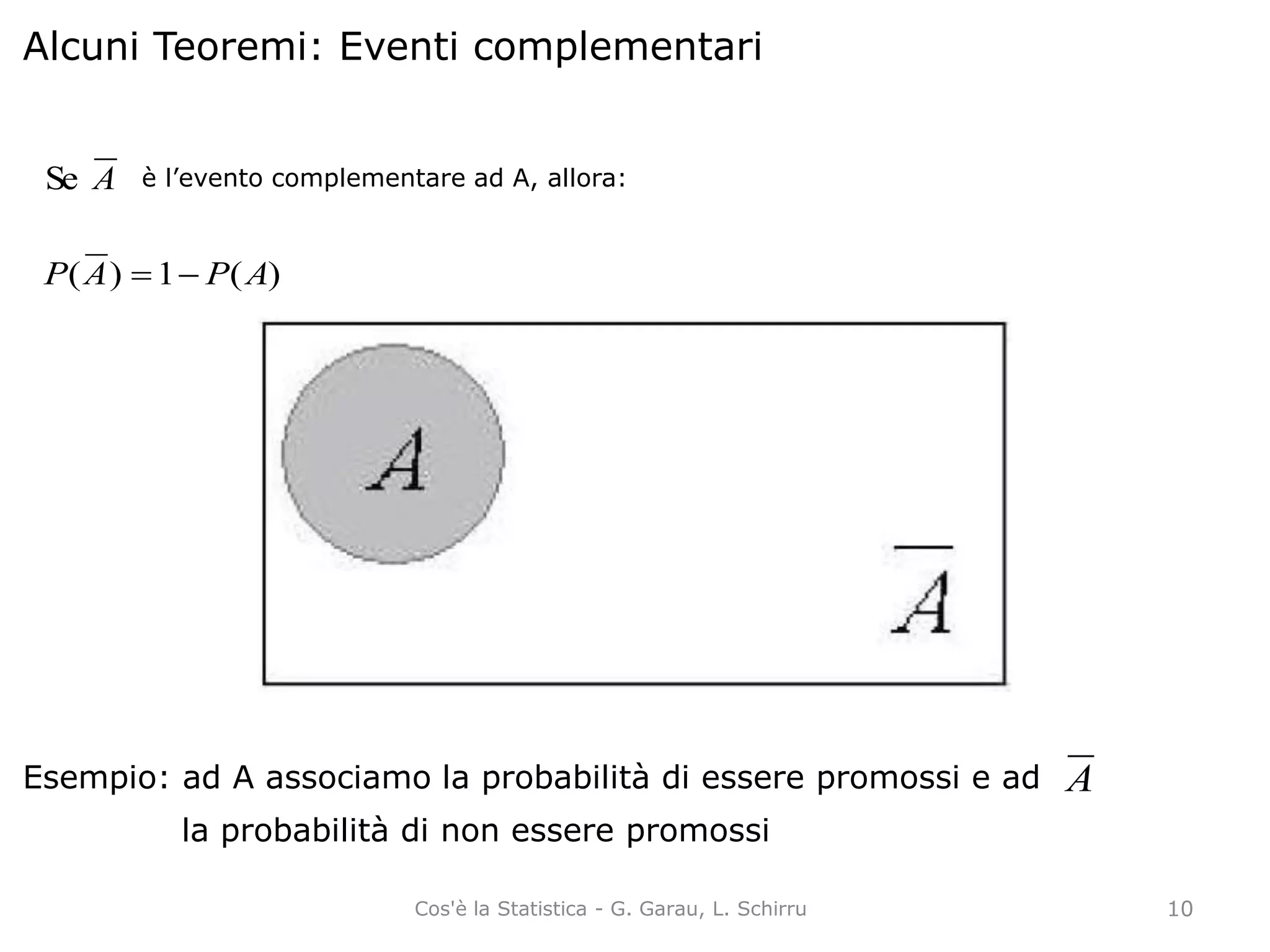
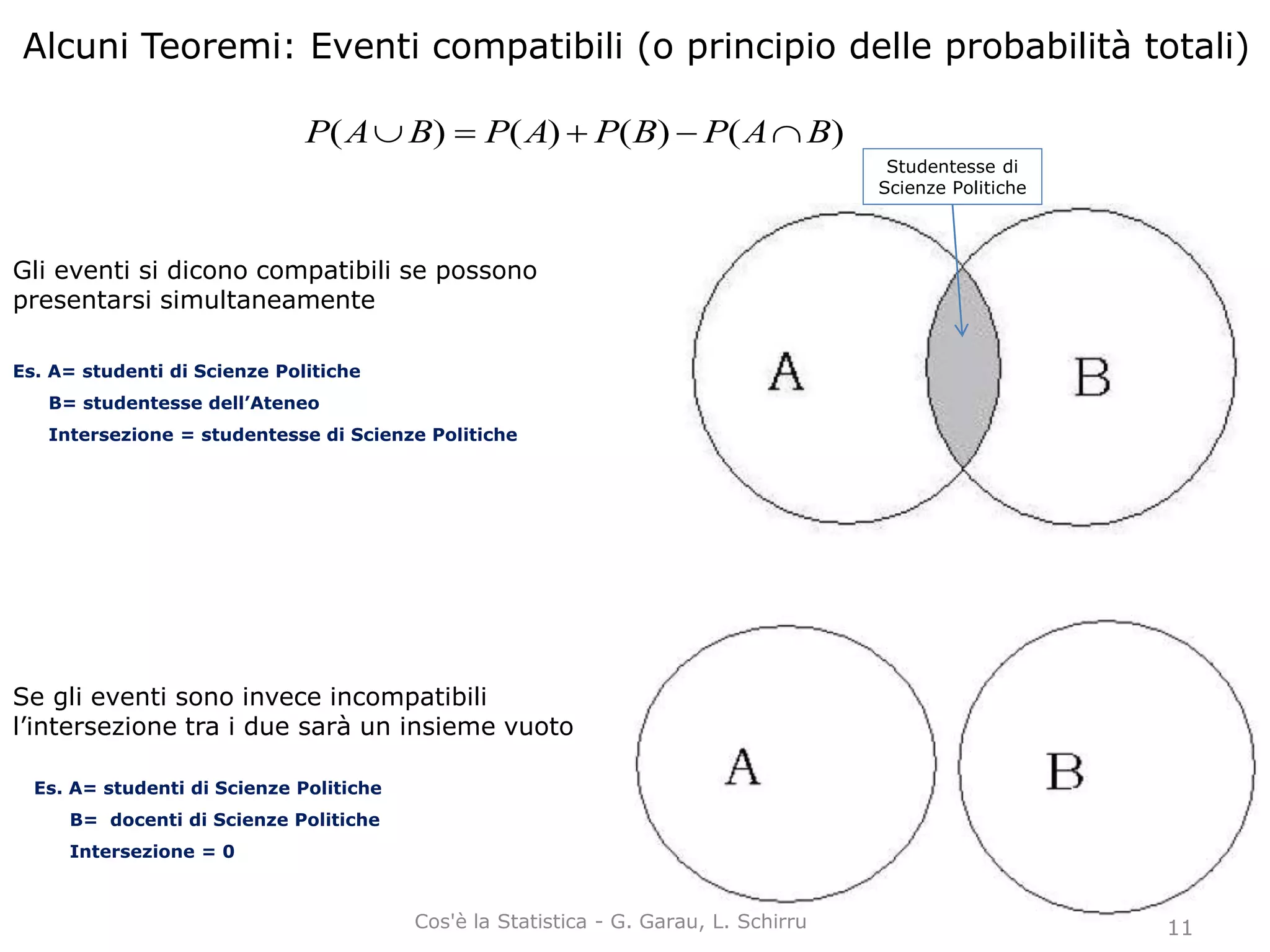
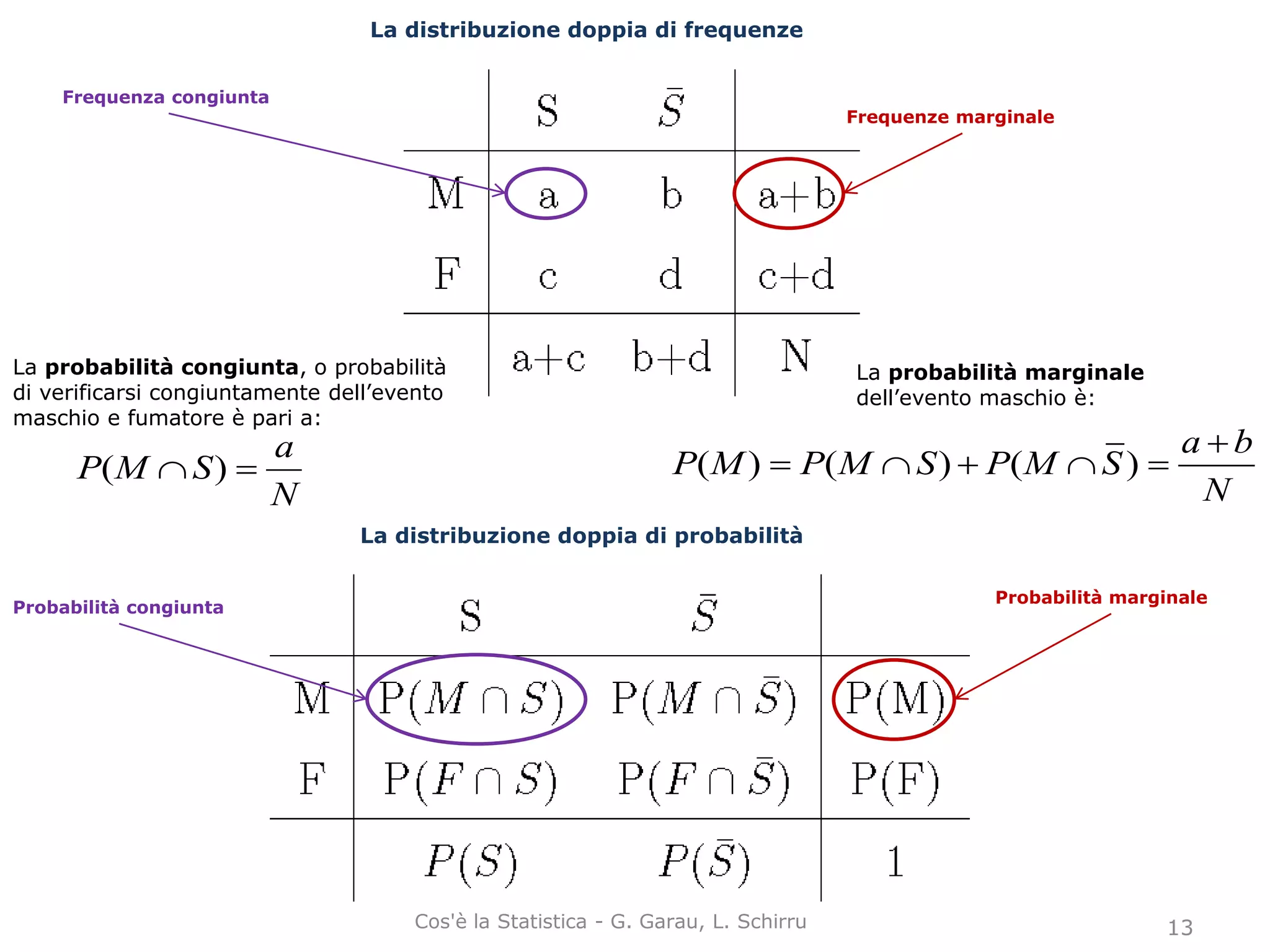
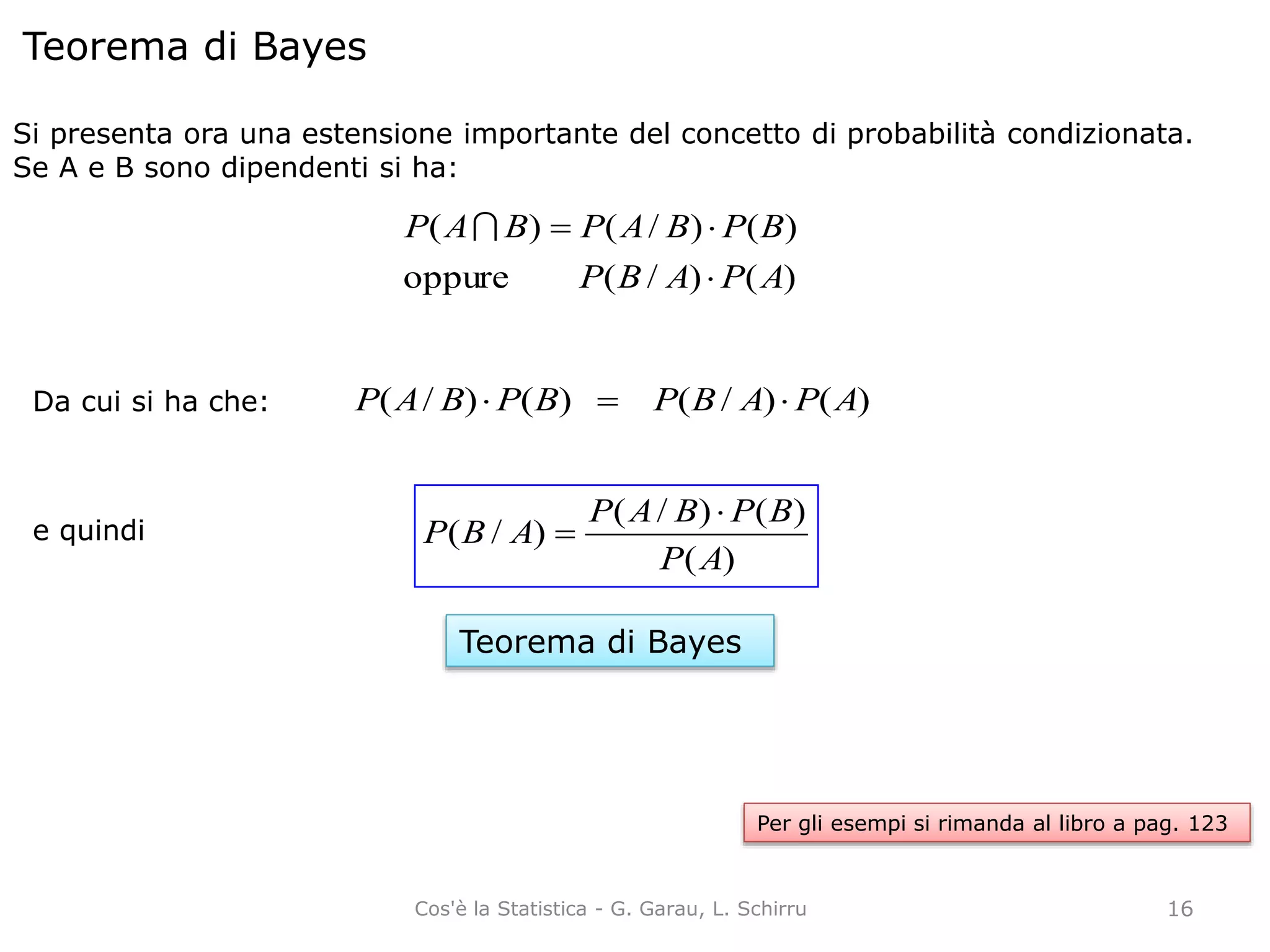
La probabilità è una misura dell'incertezza di un evento, pari a un valore tra 0 e 1. Esistono diversi approcci per calcolarla: classico (basato su equiprobabilità), frequentista (basato su frequenze relative) e soggettivo (basato sulla fiducia individuale). L'approccio assiomatico stabilisce regole generali per le misure di probabilità indipendentemente dalla loro definizione.

1. Teoria generale della probabilità
La probabilità è una misura del grado di incertezza di un evento in un
certo esperimento casuale.
E’ ragionevole misurare l’incertezza degli eventi assegnando ad essi un
numero compreso tra 0 e 1, detto probabilità di un evento.
Quanto più la probabilità è vicina a zero tanto più l’evento si verifica
raramente e quanto più la probabilità è vicina a 1 tanto più l’evento è
frequente.
Di seguito si presentano diversi modi di affrontare il problema:
-Approccio classico o a priori
-Approccio frequentista o a posteriori
-Approccio soggettivo
-Approccio assiomatico
1Cos'è la Statistica - G. Garau, L. Schirru

2. Approccio classico o a priori
Lanciando una moneta si hanno due casi possibili e a priori equiprobabili
Testa =
Croce =
Probabilità di uscita della faccia:
2
1
2
1
possibilicasi
favorevolicasi
possibilicasi
favorevolicasi
2Cos'è la Statistica - G. Garau, L. Schirru

3. Approccio classico o a priori
Lanciando un dado si hanno sei casi possibili e a priori equiprobabili
Faccia 1
Faccia 2
Faccia 3
Faccia 4
Faccia 5
Faccia 6
Probabilità di uscita di qualsiasi faccia
6
1
possibilicasi
favorevolicasi
3Cos'è la Statistica - G. Garau, L. Schirru

4. Approccio classico o a priori
La probabilità di un evento “E” è il rapporto tra il numero dei casi favorevoli
al verificarsi di “E” ed il numero totale dei casi possibili, ammesso che
questi siano equiprobabili.
possibilicasi
favorevolicasi

n
ni
Questo approccio è utilizzabile:
-quando i casi sono equiprobabili (quando tutti gli eventi hanno la stessa
probabilità di verificarsi, cioè di essere “estratti”);
-quando la conoscenza del problema permette di derivare una probabilità a priori.
Questo approccio non è utilizzabile in tutti gli altri casi.
4Cos'è la Statistica - G. Garau, L. Schirru

5. Approccio frequentista o a posteriori
La probabilità P dell’evento “E” è la frequenza relativa con cui “E” si verifica,
in una lunga serie di prove ripetute sotto condizioni simili.
n
n
EP E
n lim)(Si può scrivere
Dove nE è la frequenza assoluta associata all’evento E.
Questa definizione ci dice che la probabilità di un evento è
approssimata dalla sua frequenza relativa in un numero n infinito di
prove ripetute.
5Cos'è la Statistica - G. Garau, L. Schirru

6. Approccio frequentista o a posteriori
Lanciamo una moneta 100 volte e registriamo le frequenze relative del risultato testa e
croce.
Per n sufficientemente grande la frequenza relativa differirà di poco da quella attesa.
Rappresentiamo graficamente:
nell’asse delle ascisse il numero dei lanci e
nell’asse delle ordinate le probabilità di
avere testa.
Si nota che la probabilità dell’evento testa
è approssimata dalla sua frequenza
relativa in un numero n di prove ripetute.
6Cos'è la Statistica - G. Garau, L. Schirru

7. Approccio frequentista o a posteriori
Consideriamo ora il caso di 300 lanci di un dado:
Anche in questo caso osserviamo che al crescere di n (numero di lanci) la
frequenza relativa si approssima alla probabilità dell’evento.
7Cos'è la Statistica - G. Garau, L. Schirru

8. Approccio soggettivo
Con questo approccio si trattano gli eventi che non possono essere
considerati come eventi ripetuti e quindi non si può dare di essi
un’interpretazione in termini di frequenza.
Secondo l’approccio soggettivo la probabilità è una misura del grado di
fiducia che un individuo razionale ripone nel verificarsi di un evento.
La probabilità di un evento E, è quindi il prezzo P(E) che un individuo
giudica “equo” scommettere sull’eventualità che tale evento E si verifichi.
Con questo approccio si possono inoltre trattare le situazioni in cui si hanno
delle informazioni tali da invalidare l’idea di equiprobabilità.
Supponiamo ad esempio che si lanci una moneta truccata …
In questo caso la probabilità dell’evento testa differisce dalla
probabilità dell’evento croce.
L’importanza di questo approccio vi sarà maggiormente chiara alla fine del
modulo quando affronteremo il Teorema di Bayes
8Cos'è la Statistica - G. Garau, L. Schirru

9. Approccio assiomatico
Questo approccio si basa su degli assiomi che sono validi indipendentemente dalla definizione di
probabilità che si utilizza.
E’ quell’insieme di regole che ogni misura di probabilità deve soddisfare al di là della definizione
adottata.
Siano }...,,,{ 21 nEEE eventi rappresentativi di sottoinsiemi di uno spazio campionario 
)P(...,),(),(e 21 nEEPEP le rispettive probabilità.
Si formulano i seguenti assiomi:
1)(0  iEP
 1)(P
 ii EEP se0)(
nEEE ...,,, 21Se Sono eventi mutualmente escludentisi (indipendenti), allora
)()()()( 2121 nn EPEPEPEEEP 
1
2
3
4
L’evento è certo
L’evento è impossibile
9
Cos'è la Statistica - G. Garau, L. Schirru

10. Alcuni Teoremi: Eventi complementari
Se A è l’evento complementare ad A, allora:
)(1)( APAP 
Esempio: ad A associamo la probabilità di essere promossi e ad A
la probabilità di non essere promossi
10Cos'è la Statistica - G. Garau, L. Schirru

11. Alcuni Teoremi: Eventi compatibili (o principio delle probabilità totali)
)()()()( BAPBPAPBAP 
Gli eventi si dicono compatibili se possono
presentarsi simultaneamente
Se gli eventi sono invece incompatibili
l’intersezione tra i due sarà un insieme vuoto
Es. A= studenti di Scienze Politiche
B= studentesse dell’Ateneo
Intersezione = studentesse di Scienze Politiche
Studentesse di
Scienze Politiche
Es. A= studenti di Scienze Politiche
B= docenti di Scienze Politiche
Intersezione = 0
11Cos'è la Statistica - G. Garau, L. Schirru

12. Probabilità congiunta e probabilità marginale
Maschio
Femmina
Fuma Non Fuma
La tabella descrive, in termini di frequenze assolute o relative, una popolazione di cui si considerano
due caratteristiche: sesso e atteggiamento verso il fumo.
Spazio campionario: },,,{ SFFSSMMS
N = a+b+c+d (Totale popolazione)
Lo spazio campionario è composto dall’insieme di eventi possibili.
12Cos'è la Statistica - G. Garau, L. Schirru

13. La probabilità congiunta, o probabilità
di verificarsi congiuntamente dell’evento
maschio e fumatore è pari a:
N
a
SMP  )(
La probabilità marginale
dell’evento maschio è:
Frequenza congiunta
Frequenze marginale
N
ba
SMPSMPMP

 )()()(
La distribuzione doppia di probabilità
Probabilità marginale
Probabilità congiunta
La distribuzione doppia di frequenze
13Cos'è la Statistica - G. Garau, L. Schirru

14. Alcuni Teoremi: Indipendenza statistica (o principio delle probabilità
composte)
Date le probabilità 0)(e0)(  BPAP
allora A e B sono indipendenti se e solo se )()()( BPAPBAP 
Utilizzando i dati della tabella precedente, M e S sono indipendenti se
)()()( SPMPSMP 
In altri termini tale probabilità può essere ottenuta come prodotto delle due probabilità marginali.
14Cos'è la Statistica - G. Garau, L. Schirru

15. Alcuni Teoremi: Probabilità condizionata
Si può voler studiare la probabilità di un evento A, ipotizzando che l’evento B si sia già
verificato.
Si dice che se A e B sono sottoinsiemi di uno spazio campionario e 0)( BP allora
)(
)(
)/(
BP
BAP
BAP


La probabilità di A dato B è uguale al rapporto tra la probabilità congiunta di A e B
e la probabilità marginale di B
Questo risultato ci consente di calcolare la probabilità associata all’evento intersezione
quando A e B non sono indipendenti
)()/()( BPBAPBAP 
Facendo riferimento alla tabella di prima si può scrivere:
)()/()()/()()()( SPSMPSPSMPSMPSMPMP 
Per gli esempi si rimanda al libro a pag. 122
15Cos'è la Statistica - G. Garau, L. Schirru

16. Teorema di Bayes
Si presenta ora una estensione importante del concetto di probabilità condizionata.
Se A e B sono dipendenti si ha:
)()/(oppure
)()/()(
APABP
BPBAPBAP


Da cui si ha che: )()/()()/( APABPBPBAP 
e quindi
)(
)()/(
)/(
AP
BPBAP
ABP


Teorema di Bayes
Per gli esempi si rimanda al libro a pag. 123
16Cos'è la Statistica - G. Garau, L. Schirru

17. Teorema di Bayes: esempio
Supponiamo che il mercato delle automobili sia costituito da tre sole case produttrici: A, B,C. Le
quote di mercato sono così ripartite: A=70%, B= 25% e C= 5%.
Supponiamo anche di sapere che dopo 10 anni siano ancora funzionanti il 6% delle macchine
prodotte da A, il 22% di quelle prodotte da B e il 75% di quelle prodotte da C. Un conoscente ci
consiglia di acquistare un’auto come la sua, che funziona ancora dopo 10 anni. Quale è la
probabilità che sia un’auto prodotta da A?
Vogliamo sapere qual è la probabilità che la macchina del conoscente (che funziona ancora
dopo dieci anni) sia stata prodotta da A. Quindi vogliamo conoscere la probabilità P(A/F).
Per calcolare questa probabilità dobbiamo innanzitutto sapere quale è la probabilità che la
macchina sia funzionante P(F).
Casa produttrice Probabilità a priori
A P(A)=0.70
B P(B)=0.25
C P(C)=0.05
Casa produttrice Probabilità probative
o verosimiglianza
A P(F/A)=0.06
B P(F/B)=0.22
C P(F/C)=0.75
Probabilità che
la macchina sia
prodotta da C
Probabilità che la
macchina sia
ancora funzionante
dopo 10 anni se è
stata prodotta da C
)()()()( CFPBFPAFPFP  
17Cos'è la Statistica - G. Garau, L. Schirru

18. )(
)()/(
)/(
FP
APAFP
FAP


)()/()(
)()/()(
)()/()(
CPCFPCFP
BPBFPBFP
APAFPAFP





 La probabilità che la macchina sia funzionante
e prodotta da A, è condizionata all’essere stata
prodotta da A.
)()/()()/()()/()( CPCFPBPBFPAPAFPFP 
Per cui, P(F) è uguale a:
)()/()()/( APAFPFPFAP 
Sapendo che:
Otteniamo P(A/F) mettendolo in evidenza nella formula precedente:
Teorema di Bayes
18Cos'è la Statistica - G. Garau, L. Schirru

19. Calcoliamo ora la probabilità che la macchina, sapendo che funziona, sia prodotta da A.
%22.313122.0
1345.0
042.0
0375.0055.0042.0
042.0
)05.075.0()25.022.0()7.006.0(
7.006.0
)()/()()/()()/(
)()/(
)(
)()/(
)/(













CPCFPBPBFPAPAFP
APAFP
FP
APAFP
FAP
Calcoliamo, per curiosità anche le probabilità che la macchina, sapendo che funziona, sia
prodotta da B o da C.
%89.404089.0
1345.0
055.0
0375.0055.0042.0
055.0
)05.075.0()25.022.0()7.006.0(
25.022.0
)(
)()/(
)/(









FP
BPBFP
FBP
%88.272788.0
1345.0
0375.0
0375.0055.0042.0
0375.0
)05.075.0()25.022.0()7.006.0(
05.075.0
)(
)()/(
)/(









FP
CPCFP
FCP
19
Cos'è la Statistica - G. Garau, L. Schirru

20. I risultati ottenuti dimostrano che le probabilità a priori e quelle a posteriori possono
differire anche di molto.
Sintetizziamole in tabella:
Casa
produttrice
Probabilità a
priori
Probabilità a
posteriori
A 0.70 0.3122
B 0.25 0.4089
C 0.05 0.2788
Il teorema di Bayes trova un’importante applicazione in ambito sanitario.
20Cos'è la Statistica - G. Garau, L. Schirru

21. Esercizio 1 del libro, pag. 269.
Si effettuano due lanci consecutivi di una moneta. Definite:
a) Lo spazio campionario
b) L’evento una sola testa
c) L’evento prima faccia testa
a) Lo spazio campionario è: },,,{ CTTCCCTT
b) l’evento una sola testa è: },{ CTTCE 
c) l’evento prima faccia testa è: },{ TTTCE 
21
Cos'è la Statistica - G. Garau, L.
Schirru

22. Esercizio 3 del libro, pag. 269.
In quanti modi diversi una commissione di 25 persone può scegliere un
presidente e un vicepresidente?
Il presidente può essere scelto in 25 modi diversi e il vicepresidente in 24 modi
diversi. Ci sono in tutto N = 25 · 24 = 600 modi diversi in cui la scelta può essere
fatta.
Si è usata la formula delle disposizioni semplici per arrivare al calcolo del numero
dei modi possibili, infatti i gruppi che formiamo sono composti da 2 persone (il
presidente e il vicepresidente), quindi k = 2, mentre il numero di elementi, tra cui
poter scegliere, è 25.
Ricordiamo la formula delle disposizioni semplici:
22
Cos'è la Statistica - G. Garau, L.
Schirru

23. Esercizio 6 del libro, pag. 270.
Se un test consiste di 12 domande con risposta vero o falso, in quanti
modi diversi uno studente può svolgere l’intero test con una risposta
per ciascuna domanda?
Poiché ad ogni domanda si può rispondere in due modi, le possibilità sono
23Cos'è la Statistica - G. Garau, L. Schirru

24. Esercizio 9 del libro, pag. 270.
Quante parole si possono formare con le 5 vocali?
Il numero delle parole è dato dalle permutazioni di 5 elementi: P5 = 5! = 120
Esercizio 11 del libro, pag. 271.
Si fanno sedere 5 uomini e 4 donne in fila: in quanti modi le donne
possono occupare i posti pari?
Gli uomini possono essere sistemati in 5! modi diversi (permutazioni), le donne
in 4! modi diversi. Ciascuna sistemazione degli uomini può essere associata ad
ogni sistemazione delle donne, quindi il numero complessivo di sistemazioni è:
24Cos'è la Statistica - G. Garau, L. Schirru

25. Esercizio 13 del libro, pag. 271.
Quante squadre di calcio si possono formare con 30 giocatori?
Il numero è dato dalle combinazioni di 11 giocatori scelti nell’insieme di 30
25Cos'è la Statistica - G. Garau, L. Schirru

26. Esercizio 15 del libro, pag. 271.
Nel gioco del lotto vengono estratti, senza rimetterli ogni volta nell’urna, 5 numeri
compresi fra 1 e 90. Le estrazioni avvengono su 10 città o “ruote” diverse, e bisogna
precisare su quale ruota si gioca.
a. Trovare il numero di tutte le possibili cinquine relative ad ognuna delle ruote.
b. Quante sono le possibili estrazioni che ci fanno vincere se abbiamo giocato ad
esempio l’ambo {13, 48} su una certa ruota?
a. Il numero di tutte le possibili cinquine è dato dalle combinazioni
b. Cerchiamo il numero di cinquine che contengono 13 e 48: gli altri numeri
estraibili sono i numeri da 1 a 12, da 14 a 47, da 49 a 90, in tutto 88 numeri;
calcoliamo le combinazioni di 88 numeri a gruppi di 3:
26Cos'è la Statistica - G. Garau, L. Schirru