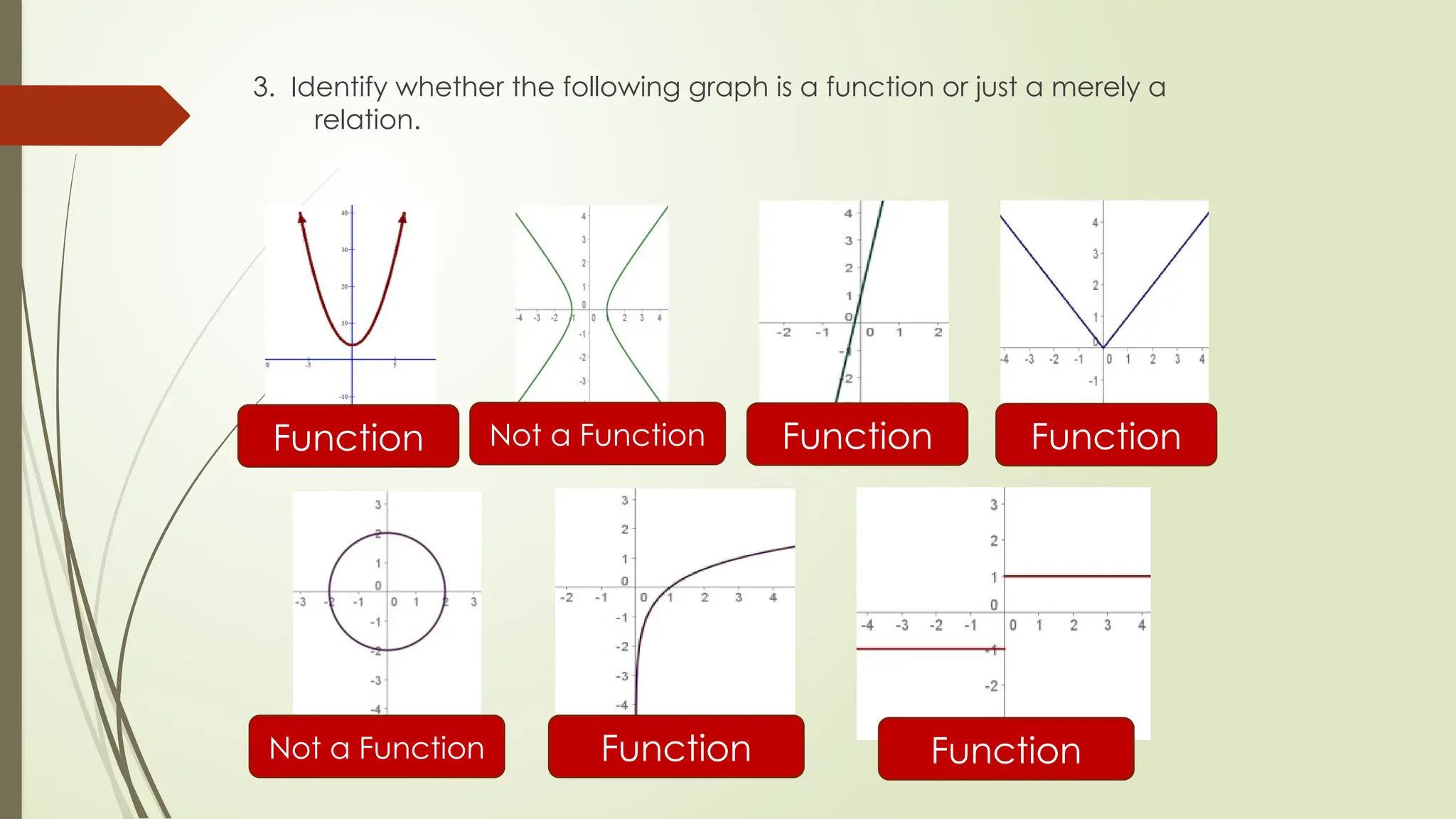
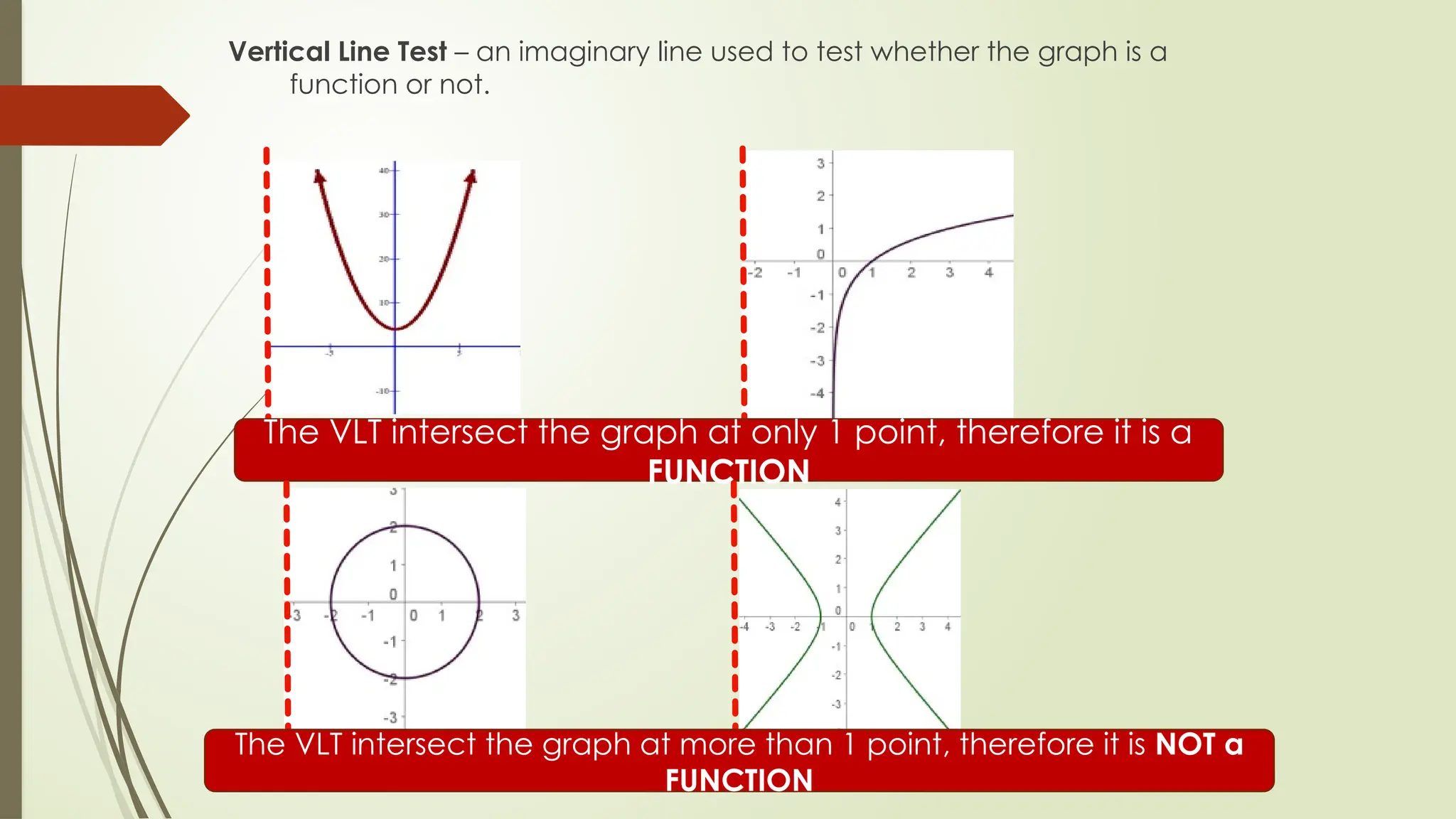
The document explains the concepts of relations and functions, including definitions, examples, and ways to express them. It details how to identify the domain and range of relations, differentiate between functions and relations, and includes practical examples and assessments of real-life situations related to these mathematical concepts. The functions are characterized as special relations where each input corresponds to a unique output, with various forms of expression such as set notation, graphs, and equations.

1. Functions and
its Graph

2. Relation
Objectives:
• Define a relations;
• identify domain and range of a
relation.

3. WORD HUNT
Find as many
words as you can
that can be
associated on the
topic Function and
Relation.

4. WORD HUNT
Find as many
words as you can
that can be
associated on the
topic Function and
Relation.
1. Function
2. Relation
3. Domain
4. Range
5. Set
6. Table
7. Mapping
8. Graph
9. Equation
10.Input
11.Output

5.  Getting Ready
To be able to save money and energy, just dial
“RENT CAR”.

6. Relation is referred to as any set of ordered
pair. Conventionally, It is represented by the
ordered pair ( x , y ). x is called the first element
or x-coordinate while y is the second element or
y-coordinate of the ordered pair.
DEFINITION
Relation is a rule that relates values from a set
of values (called the domain) to the second set of
values (called the range)

7. Ways of Expressing a Relation
5. Mapping
2. Tabular form
3. Equation
4. Graph
1. Set
notation

8. .
Example: Express the relation y = 2x
when x= 0,1,2,3 in 5 ways.
1. Set notation
(a) S = { ( 0, 0) , ( 1, 2 ) , ( 2, 4 ), ( 3, 6) }
or
(b) S = { (x , y) / y = 2x, x = 0, 1, 2, 3 }
2. Tabular
form
x 0 1 2 3
y 0 2 4 6

9. 3. Equation: y = 2x
4. Graph
y
x
5
-4 -2 1 3 5
5
-4
-2
1
3
5
-5 -1 4
-5
-1
4
-3
-5
2
2
-5
-3
●
●
●
1 2
2 4
6
3
0 0
x y
5. Mapping

10. DEFINITION: Domain and Range
All the possible values of x is called the
domain and all the possible values of y is called
the range. In a set of ordered pairs, the set of first
elements and second elements of ordered pairs is
the domain and range, respectively.
Example: Identify the domain and range of the following
relations.
1.) S = { ( 4, 7 ),( 5, 8 ),( 6, 9 ),( 7, 10 ),( 8, 11 ) }
Answer : D: { 4,5,6,7,8} R:{7,8,9,10,11}

11. 2.) S = { ( x , y ) / y = | x | ; x  R }
Answer: D: all real nos. R: all real nos. > 0
3) y = x 2
– 5
Answer. D: all real nos. R: all real nos. > -5
4) | y | = x
Answer: D: all real nos. > 0 R: all real nos.
)
,
( 
 )
,
0
[ 
)
,
( 
 )
,
5
[ 

)
,
0
[  )
,
( 


12. 5.
7.
8.
6.
X 0 1 2 3 4
y 6 8 10 12 14
X 2 1 0 1 2
y -8 -4 0 4 8
X -4 -2 0 2 4
y 1/8 1/4 1/2 1 2
X 0 2 4 2 0
Y 1 1/2 0 1/2 1
Domain: {0, 1, 2, 3, 4}
Range: {6, 8, 10, 12, 14}
Domain: {0, 1, 2}
Range: {-8, -4, 0, 4, 8}
Domain: {-4, -2, 0, 2, 4}
Range: {1/8, ¼, ½, 1, 2}
Domain: {0, 2, 4}
Range: {0, ½, 1}

13. A
B
C
D
E
F
1
2
3
4
5
6
9. Star
Square
Circle
Triangle
Diamond
Oblong
0
1
2
3
4
5
10.
2
3
A
B
C
D
E
F
11.
12. 13. 14.
Domain: {A,B,C,D,F}
Range: {1, 2, 4, 5, 6}
D: {star,square,circle,triangle,
diamond, oblong}
Range: {1, 2, 3, 4}
Domain: {2, 3}
Range: {A, B, C, D, E, F}
Domain: {x|x  ℜ}
Range: {y|y  ℜ}
Domain: {x| x  ℜ , -2 ≤ x ≤
+2}
Range: {y| y  ℜ , -2 ≤ y ≤
+2}
Domain: {x|x  ℜ+
}
Range: {y|y  ℜ}

14. RememberThis!
Identifying Domain and Range
1. Set of Ordered Pairs:
a. Domain – a set of all first coordinates of the ordered pairs.
b. Range – a set of all second coordinates of the ordered pairs
2. Tabular Form:
a. Domain – a set of all x-values.
b. Range – a set of all y-values.
3. Mapping Diagram:
a. Domain – a set of all elements on the first group.
b. Range – a set of all elements on the second group.
4. Graphing:
a. Domain – a set of all values on the x-axis covered by the graph.
b. Range – a set of all values on the y-axis covered by the graph.

15. Let Us Try This!
Determine domain and range of the following:
1.S = {(a,2), (b,4), (c,6), (d,8), (e,10)}
2.S = {(-6,9), (6,-9), (9,6), (-9,6)}
3. 4.
5. 6.

16. Let Us Try This!
Determine the domain and range of the
following.
7.y = 4x2
+ 12
8.y = 14 - x
9. 10.




2
3
4
5
6
7






1
3
5
2
4

17. Function
Objectives:
1. define intuitively a function;
and
2. identify real life examples of a
function including piecewise
functions;

18. Review:
1.What is a relation?
2.In a relation, how can you identify a
independent variable and dependent
variable?
3.What is another name you can give to
independent variable? Dependent ariable?
4.Give five examples of relation citing the
independent variable and dependent variable.
5.For each example, can you identify if the
relation works or valid?

19. Definition: Function
A function is a special relation such that
every first element is paired to a unique second
element.
It is a set of ordered pairs with no two pairs
having the same first element.

20. Real Life Examples of Function

21. Real Life Examples of Function

22. Real Life Examples of Function

23. Real Life Examples of Function

24. Real Life Examples of Function

25. Real Life Examples of Function

26. Piecewise or Split Function

27. Piecewise or Split Function

28. Real Life Examples of Piecewise or Split
Function

29. Real Life Examples of Piecewise or Split
Function

30. Real Life Examples of Piecewise or Split
Function

31. Real Life Examples of Piecewise or Split
Function

32. Let’s Get Real!
Tell whether the following situation describes a function or not.
1. The amount of postage placed on a first-class letter depends on the weight of the letter.
2. The temperature of a cup of coffee depends on how big the cup is.
3. The height which a football attains depends upon the number of seconds after it was kicked.
4. The number of pages read is related to the number of words written on every page.
5. The speed of the bullet depends on its acceleration.
6. The amount in peso of a $100 bill is related to the country’s inflation rate.
7. The overtime pay of an employee is related to the number of hours he worked overtime.
8. The amount paid for a long distance call depends on how long the call is made.
9. The amount of monthly internet bill depends on the amount of data being used for the post
paid consumers.
10.The amount of tax a company pays depends upon its net profit for the year.

33. How to Differentiate a Function
from a Relation?

34. Differentiating Function from a
Relation
Objectives:
1. differentiate a function from
a relation; and

35. 
x
y sin

1
3

x
y
One-to-one and many-to-one functions
Each value of x maps to only
one value of y . . .
Consider the following graphs
Each value of x maps to only one
value of y . . .
BUT many other x values map to
that y.
and each y is mapped from
only one x.
and
Functions

36. One-to-one and many-to-one functions
is an example of
a one-to-one function
1
3

x
y
is an example of
a many-to-one function

x
y sin


x
y sin

1
3

x
y
Consider the following graphs
and
Functions
One-to-many is NOT a function. It is just a
relation. Thus a function is a relation but a relation
could never be a function.

37. 1. Identify whether the given set is a
function or just a merely a relation.
A = {(-1,-1), (0,1), (1,0), (1,1)}
B = {(-1,-1), (0,1), (1,0), (2,-2)}
C = {(-1,-1), (0,1), (1,0), (2,-1)}
D = {(-1,-1), (0,1), (1,0), (0,-1), (1,-1)}
Not a Function
Function
Function
Not a Function

38. 2. Identify whether the given table
is a function or just a merely a
relation.
Function
Not a Function
Function
Not a Function
X 0 1 2 3 4
y 6 8 10 12 14
X 2 1 0 1 2
y -8 -4 0 4 8
X -4 -2 0 2 4
y 1/8 1/4 1/2 1 2
X 0 2 4 2 0
Y 1 1/2 0 1/2 1

39. 3. Identify whether the following graph is a function or just a merely a
relation.
Function
Not a Function
Function
Not a Function
Function Function
Function

40. Vertical Line Test – an imaginary line used to test whether the graph is a
function or not.
The VLT intersect the graph at only 1 point, therefore it is a
FUNCTION
The VLT intersect the graph at more than 1 point, therefore it is NOT a
FUNCTION

41. Many-to-one
4. Identify whether the given illustration describes
a function or just a merely a relation.
Noel
Joel
Kim
Julie
Nina
Joy
Bird
Cat
Dog
Turtle
Mice
Pig
Star
Square
Circle
Triangle
Diamond
Oblong
0
1
2
3
4
5
A
B
C
D
E
F
1
2
3
4
5
6
2
3
A
B
C
D
E
F
Function Function Not a Function
Not a Function
One-to-one Many-to-many
One-to-many

42. 5. Identify whether the given equation is
a function or just a merely a relation.
a. y = 4x + 8
b. 4x2
+ 9y2
= 16
c. y = 2x2
– 3x + 16
d. x = 3y3
+ 10
e. y =
f. y =
Not a Function
Function
Function
Not a Function (if the range is a set of real
numbers)
Not a Function
Function
Function (if the range is a set of positive real
numbers)

43. How to Determine a Function Using the Five
Ways in Representing a Relation?
 By Set Notation - There should be no duplication on
the first coordinate
 By Tabular Form – There should be no duplication
on the x-values.
 By Graphing – The Vertical Line Test (VLT) should
intersect the graph at only one point.
 By Mapping (Arrow Diagram) – One-to-one
Correspondence/ Many-to-one Correspondence
 By Equation – The exponent of the dependent
variable (y) is one or odd.

44. Let Us Try This!
Determine whether the following is a function or just
a mere relation.
1.S = {(a,2), (b,4), (c,6), (d,8), (e,10)}
2.S = {(-6,9), (6,-9), (9,6), (-9,6)}
3. 4.
5. 6.

45. Let Us Try This!
Determine whether the following is a
function or just a mere relation.
7.y = 4x2
– 2x + 12
8.x2
– 3y2
= 14
9. 10.




2
3
4
5
6
7






1
3
5
2
4

46. Identify which of the following
relations are functions.
1) S = { ( 4, 7 ), ( 5, 8 ), ( 6, 9 ), ( 7, 10 ), ( 8, 11 ) }
2) S = { ( x , y ) / y = | x | ; x   }
3) y = x 2
– 5
4) | y | = x
5) x2
– 4x = y2
– 3x 8.
2
x
x
2
y


6)
1
x
y 

7)
X 1 -1 11 -1
y 12 4 -6 4
X 1 -1 11 -11
y 4 0 44 -44
9.

47. Identify which of the following
relations are functions.
A
B
C
D
E
2
3
4
5
W
X
Y
Z
1
3
5
2
4
10. 11.
12. 13.

48. Evaluating Functions
Objectives:
1. Evaluate a function given
a value of x.

50. Meet best friends Emily and Anton.
They have formed a partnership. Anton,
being the creative one, makes costume
jewelry. Emily, being business-minded, markets the jewelry Anton
makes. In a recent month, they spent Php1,000 on raw materials to
make 50 pieces of jewelry and sell each for Php25.00. assuming that
they are not required to pay a sales tax, their net profit depends on the
number of pieces of jewelry sold.
1. The problem includes three constants: the fixed cost of raw materials
(Php1,000), the selling price for each piece (Php25.00), and the total
number of jewelry pieces made (50).
SITUATION:

51. SITUATION:
Number of
Pieces of
Jewellery
Sold (n)
Net Profit in
Pesos (Php)
0 -1,000
10 -750
20 -500
25 -375
30 -250
45 125
2. Let us use n to represent the number
of pieces of costume jewelry sold and
P for the net profit in pesos.
a. What should be the greatest value
of n? The greatest value of P?
b. What should be the least value of
n? The least value of P?
3. Some of the data for selling the
costume jewelry is shown in the table
at the right.

52. SITUATION:
4. Show the function machine that clearly shows the input, the
process, and the output after selling the costume jewelry is
given as follows.
5. Write the equation that shows algebraically how to compute
the net profit given the number of pieces of jewelry sold.
6. If there are 40 pieces of jewelry sold, how much should be
the profit?
Number of jewelry (n) x 25 - 1000
f(x) = 25x - 1000

53. THE FUNCTION NOTATION:
The name of a
function is f.
Other letters
may also be
used to name a
function.
f(x) is read as “f of x”,
and this represent the
value of the function at
x.
The function notation y = f(x) tells you that y is a function of x. if
there is a rule relating y to x, such as y = 3x +1, then you can also
write:
f(x) = 3x + 1

54. DEFINITION: Function Notation
•Letters like f , g , h and the likes are
used to designate functions.
•When we use f as a function, then for
each x in the domain of f , f ( x )
denotes the image of x under f .
•The notation f ( x ) is read as “ f of x ”.

55. EXAMPLE:
Evaluate each of the following function.
1. If f(x) = x + 8, find:
a. f(4) b. f(-2) c. f(-x) d. f(x + 3)
e. f(x2
- 3)
2. If g(x) = x2
– 4x, find:
a. g(-5) b. g(0) c. g(4) d. g(2x)
e. g(x - 1)

56. MORE EXERCISES:
Evaluate each of the following function.
1. If f ( x ) = x + 9 , what is the value of f ( 6 ) ?
2. If g ( x ) = 2x – 12 , what is the value of g (– 2 )?
3. If h ( x ) = x 2
+ 5 , find h ( x + 1 ).
4. If h ( t ) = 3t + 5 and t(x) = x2
+ 6, find h(x).
5. If k ( t ) = 6t + 5, t(s) = ( s + 1 ) and s = 9,
find k( t ) and t( s ).

57. ASSESSMENT:
Evaluate each of the following function.
1. If f(x) = 9 – 6x, find:
a. f(-1) b. f(2/3) c. f(-3+x) d. f(2x-1)
2. If Given f(x) = , find
a. f(2) b. f(0) c. f(2 – x) d. f(a + b)

58. Evaluating Piecewise Functions
Objectives:
1. Evaluate a piecewise
function given a value of x.

59. Piecewise Defined Function
if x < 0





1
x
x
)
x
(
f
.
1
2
0
x 
if 







2
)
2
x
(
1
x
x
3
)
x
(
f
.
2
A piecewise function is defined by different
formulas on different parts of its domain.
Example:
; x < 2
; x = 2
; x > 2

60. You plan to sell cupcakes to raise funds. A bakery charges you
Php 15.00 for the first 100 cupcakes. After the first 100 cupcakes
you purchase up to 150 cupcakes, the bakery will lower the price
to Php13.00 per cupcake. After you purchase 150 cupcakes, the
price will decrease to Php 10.00 per cupcake.
a.write the piecewise function
that describes what the bakery
charges on the cupcakes.
b.Graph the function
SITUATION:

61. Piecewise Defined Function
if x<0
Find the value of the
following:
f(-2), f(-1), f(0), f(1), f(2)
EXAMPLE: Evaluate the piecewise function at the
indicated values.





1
x
x
)
x
(
f
.
1
2
0
x 
if








2
)
2
x
(
1
x
x
3
)
x
(
f
.
2
find the value of the
following:
0
x 
if
if
if
2
x
0 

2
x 

62. Let’s Try This!
Find the value of the
following:
f(-5), f(-1), f(0), f(1), f(5)








1
;
1
1
;
1
2
)
(
.
1
2
x
x
x
x
x
f








3
2
5
1
4
)
(
.
2
2
x
x
x
f
find the value of the
following:
f(-5), f(0), f(1), f(5)
if x > 2
if -2 ≤ x ≤ 2
if x < -2

63. A. Evaluate each function at the indicated values of the
independent variable and simplify the result.
1. Given f(x) = 9 – 6x, find
a. f(-1) b. f(2/3) c. f(-3 + x) d. f(2x – 1)
2. Given f(x) = , find
a. f(2) b. f(0) c. f(2 – x) d. f(2a)
3.

64. Operations on Functions
•Addition of Functions
If f and g are
functions, their sum is a
function defined as
(f + g)(x) = f(x) + g(x)
•Subtraction of Functions
If f and g are
functions, their difference
is a function defined as
(f - g)(x) = f(x) - g(x)
•Multiplication of Functions
If f and g are functions,
their product is a function
defined as
(f ● g)(x) = f(x) ● g(x)
•Division of Functions
If f and g are functions,
their quotient is a function
defined as
(f ÷ g)(x) = f(x) ÷ g(x)

65. Let’s try this!
Given the following functions
f(x) = 2x
g(x) = 4x – 5
h(x) = x2
+ 1.
Find the following:
a. (g + h)(x) b. (h - g)(x)
c. (h ● h)(x) d. (g ● h)(x)
e. (g ÷ f)(x) f. (h ÷ g)(x)

66. Let’s try this!
1. If f(x) = 2x2
– 1 and g(x) = x2
+ x, find:
a. (f + g)(x) b. (f – g)(x)
c. (f ● g)(x) d. (f ÷ g)(x)
2. If k(x) = 3x2
– 5 and h(x) = 2x + 6, find:
a. (k + h)(x) b. (k – h)(x)
c. (k ● h)(x) d. (k ÷ h)(x)

67. Given f(x) = 11– x and g(x) = x 2
+2x –10 evaluate
each of the following functions.
1. f(-5)
2. g(2)
3. (f g)(5)
4. (f - g)(4)
5. f(7)+g(x)
6. g(-1) – f(-4)
7. (f ○ g)(x)
8. (g ○ f)(x)
9. (g ○ f)(2)
10.(f○ g)

)
(x 2
Let Us Try This!

68. 

69. Composition of Functions
•Composite Functions
If f and g are functions, the composite function f
with g is defined as
(f ○ g)(x) = f(g(x))
The domain of (f ○ g)(x) is the set of all x such
that
a. x is the domain of g; and
b. g(x) is the domain of f.
Let f(x) = √x, g(x) = 4x2
– 5x, and h(x) is x + 1. Find the
following:
a. (g ○ h)(x) b. (h ○g)(x)
c. [h ○ h](x) d. [f ○ (g + h)](x)

70. Let’s Try This!

71. 1.Given f(x) = x2
– 2 and g(x) = x + 2.
Find: a) (f ○ g)(x) b) (g ○f)(x)
c) (f ○ g)(-1) d) (g ○f)(2)
2.Given f(x) = x - 8 and g(x) =
Find: a) (f ○ g)(x) b) (g ○f)(x)
c) (f ○ g)(0) d) (g ○f)(1)

72. 1.Given f(x) = 3x – 1, g(x) = x2
+ 1,
and h(x) = .
Find:
a. (f + g)(2) b. (g – f)(x)
c. (f ●g)(x) d. (g ÷ f)(1)
e. (h ○ f)(-1) f. (h ○ g)(0)
g. (f ○ g)(x) h. (g ○ f)(c)

73. 

74. Problem Solving
Steps in Problem Solving:
1. READ the problem carefully and draw the
picture that conveys the given information.
• Identify what information is given.
• Identify what you are asked to find.
•Choose a variable to represent one of the
unspecified number in the problem.
2. PLAN the solution. After defining the variables,
find a word sentence to suggest an equation
for the number(s). use the expressions to
replace the word sentence by an equation.

75. Problem Solving
Steps in Problem Solving:
3. SOLVE the problem. To solve the equation,
familiarize yourself with the properties of equality
and to use PEMDAS rule for series of operations.
4. EXAMINE the solution. Use the solution of the
equation to write a statement that settles the
problem. Check that the conclusion agrees with
the problem situation or satisfies all conditions of
the problem.

76. Problem Solving
Example:
1. The perimeter of a rectangle is 100 cm.
express the area of the rectangle in terms of
the width x.
2. A piece of wire x cm long is bent into the
shape of a circle. Express the area (A) of the
circle in terms of x, the circumference.
3. Express the length of the radius of a circle as
a function of the area of the circle.

77. Problem Solving
Example:
4. Mang Juan wanted to build a fence for his ducks
beside the river. The fence is rectangular in shape
with an open side on the river. What is the
maximum area made by 100 meters of fencing?
5. The length of a rectangle is twice its width. When
the length is increased by 5 and the width is
decreased by 3, the new rectangle will have a
perimeter of 52. Find the dimensions of the original
rectangle?

78. Problem Solving
Let’s Try This:
1. The perimeter of a rectangle is 24 cm.
Express the area of the rectangle in
terms of the width x.
2. The area of a rectangle is 85 cm2
.
Express the perimeter of the rectangle
as a function of the width x.
3. A piece of wire y cm long is bent into a
circle. Express the area of the circle as a
function of the circumference y.

79. Problem Solving
Let’s Try This:
4. Two years ago, Nelly was three times as old as
her nephew was then. In five years, Nelly will
be only two times as old as her nephew. How
old is each?
5. The height of a projectile fired upward is
given by the formula S = vt – t2
, where S is the
height, v is the initial velocity, and t is the time.
Find the time for a projectile to return to earth
if it has an initial velocity of 98 mps.

80. E V A L U A T I O N
Problem Solving:
1a. The perimeter of a rectangle is 160 cm.
Express the area of a rectangle in terms of
width, x.
b. What is the area of a rectangle if its width is 8
cm?
2a. A piece of wire, x cm long is bent into the
shape of a circle. Express the area of the
circle in terms of x.
b. If the wire is 20 cm long, what would be the
area of a circle made by the wire?

81. E V A L U A T I O N
1a. The perimeter of a rectangle is 100 cm. Express
the area of a rectangle in terms of width, x.
b. What is the area of a rectangle if its width is 6 cm?
2a. A piece of wire, x cm long is bent into the shape of a
circle. Express the area of the circle in terms of x.
b. If the wire is 314 cm long, what would be the area of
a circle made by the wire?
3a. The area of a rectangle is 1601 cm2
. Express the
perimeter of the rectangle as a function of the width,
x.
b. If the width of a rectangle is 10 cm, Find the
perimeter.

82. E V A L U A T I O N
1a. The area of a rectangle is 400 cm2
. Express
the perimeter of a rectangle in terms of
length, x.
b. What is the perimeter of a rectangle if its
length is 24 cm?
2a. Express the circumference of a circle in terms
of its area.
b. If the area of a circle is 31,416cm2
, what
would be its circumference?
3. Harry is 20 years older than Ivan. Five years
from now, Ivan will be 3/5 as old as Harry.
How old is each now?