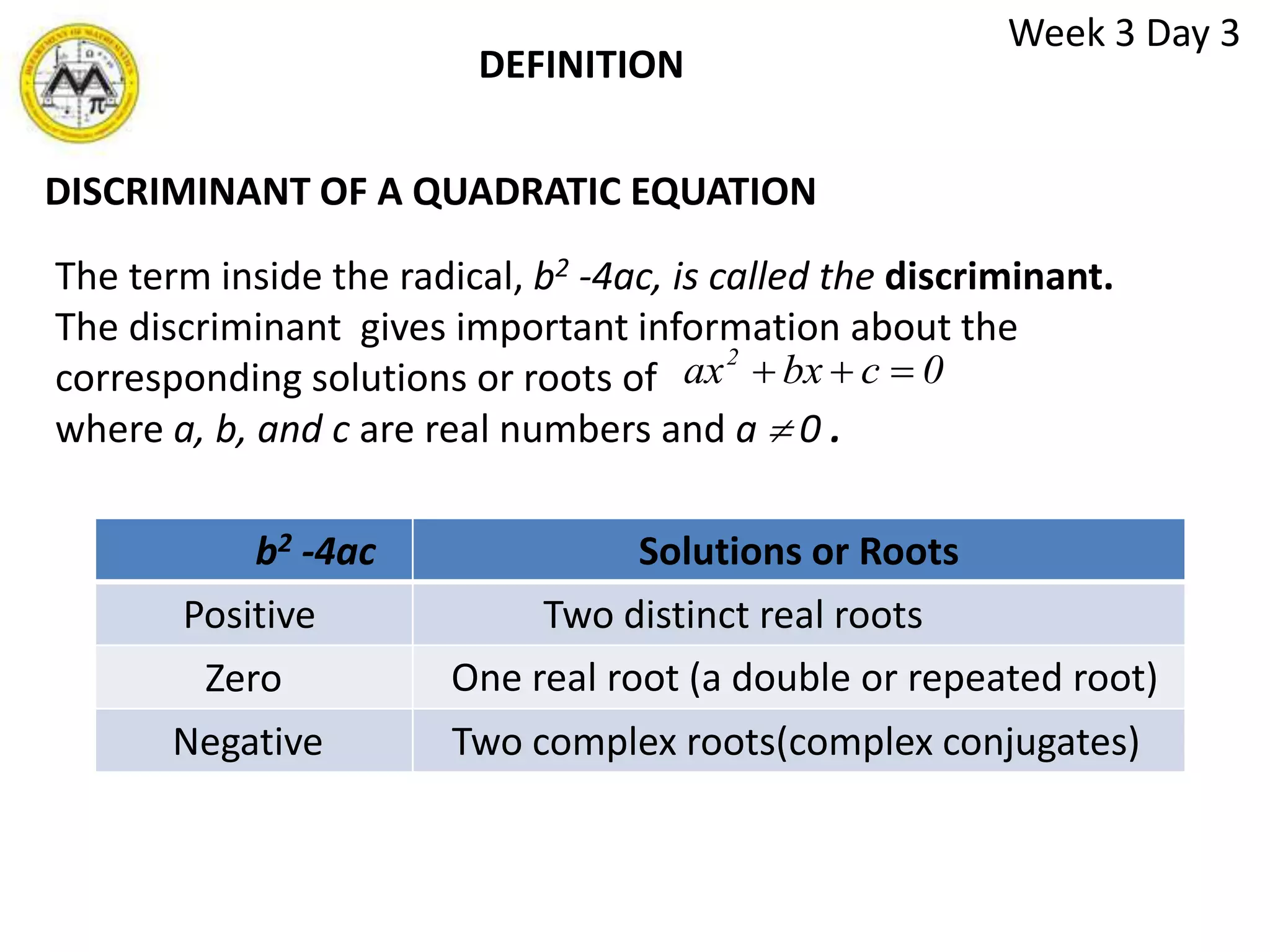
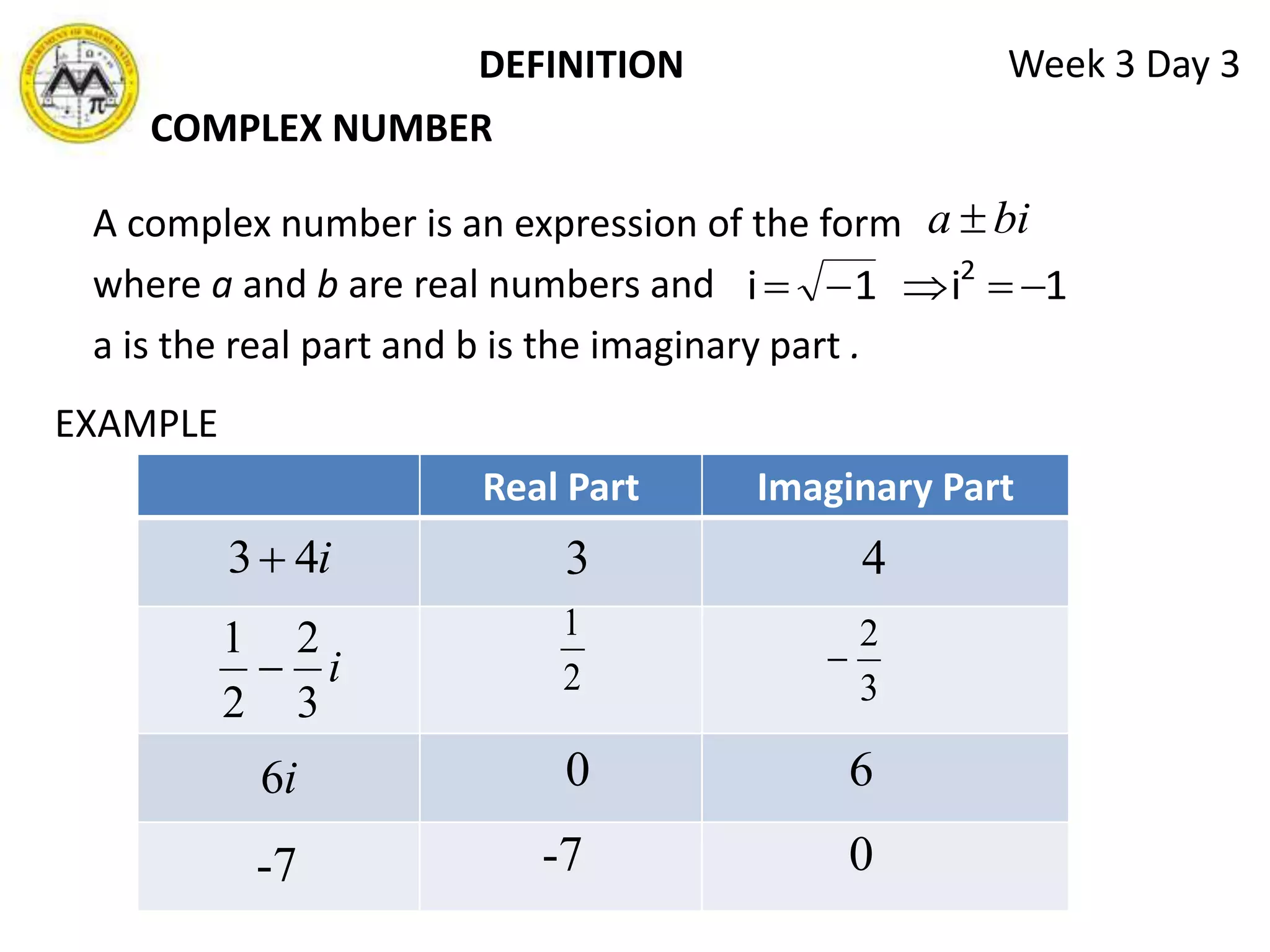
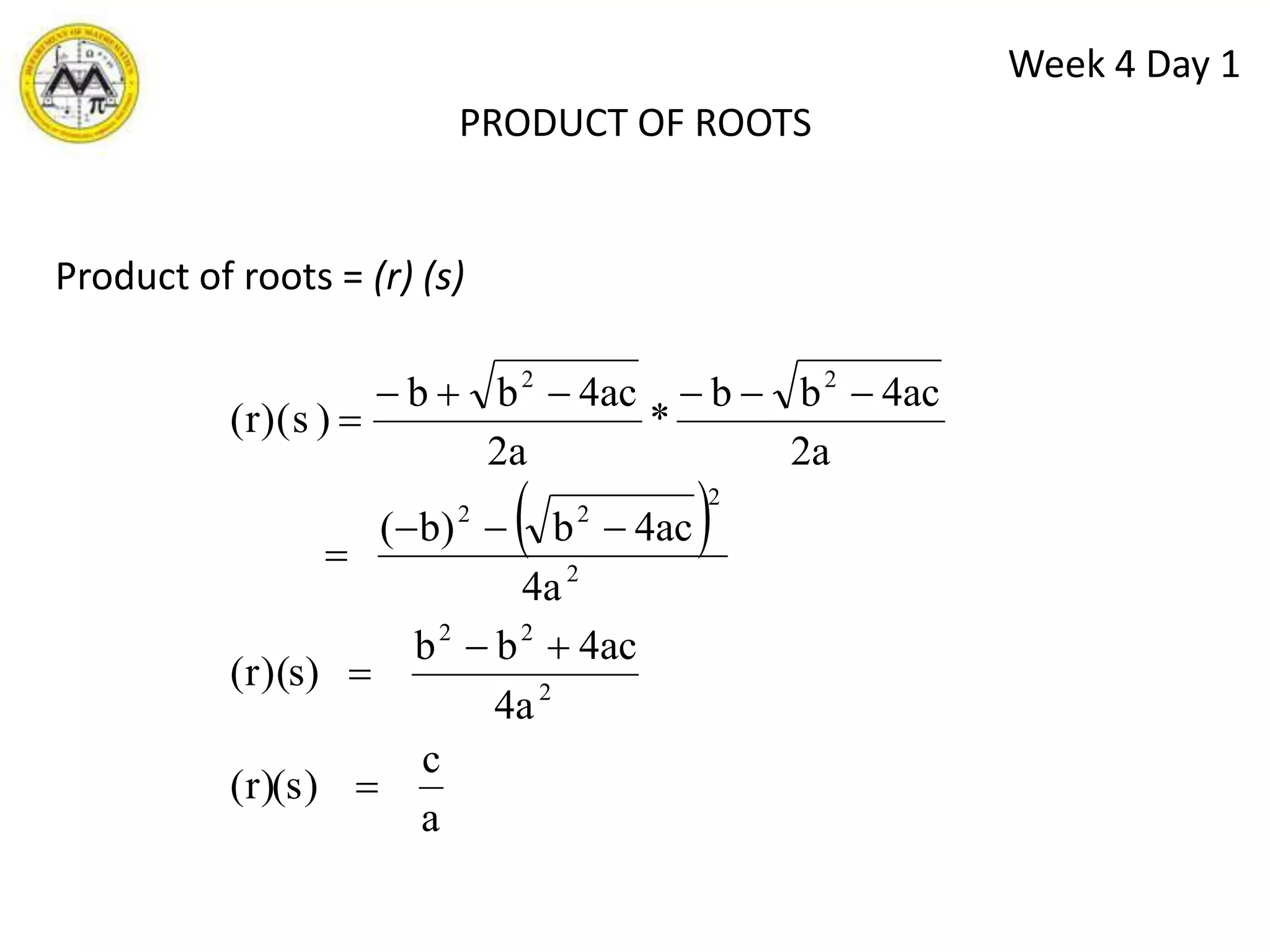
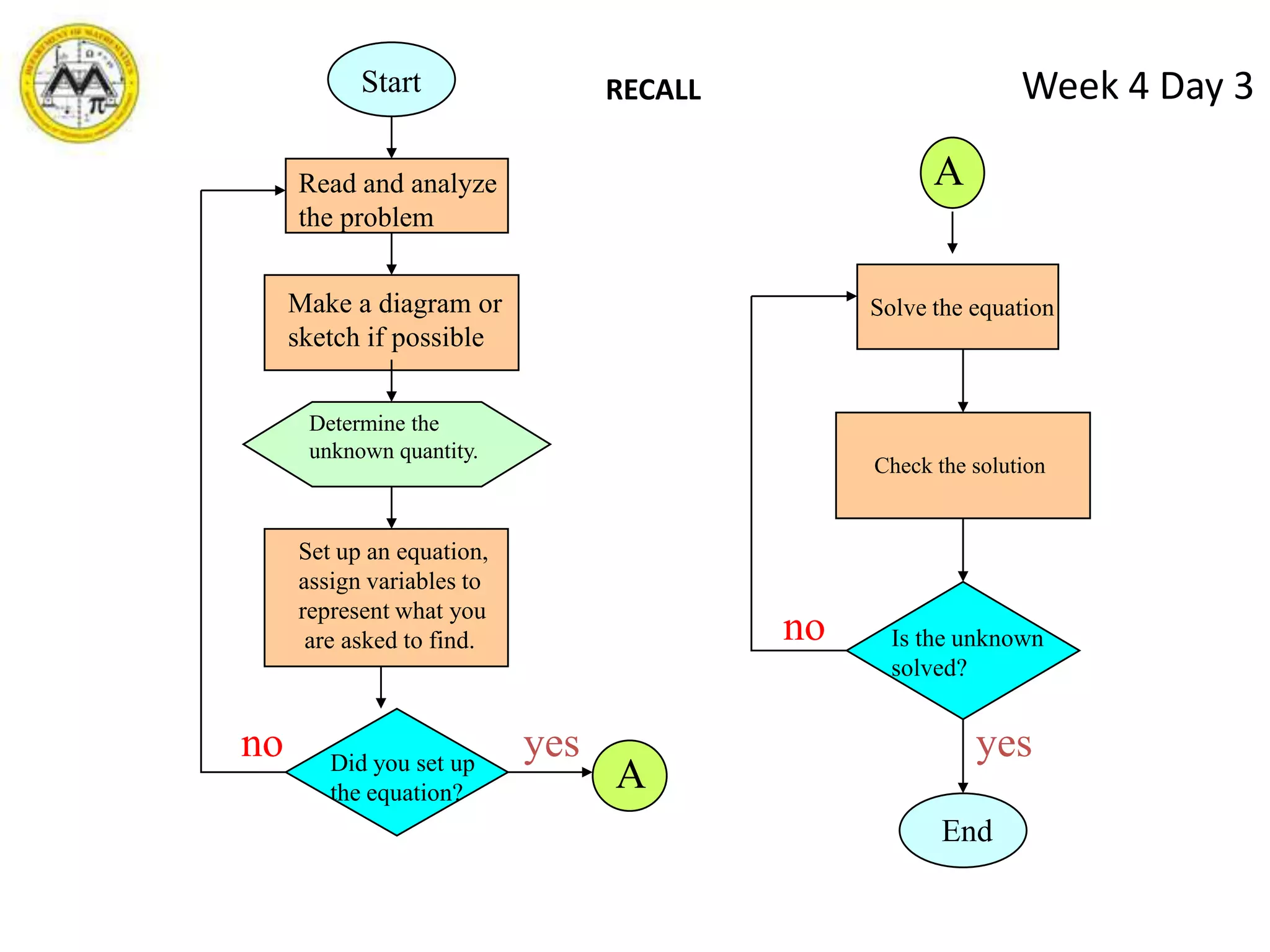
The document discusses various methods for solving quadratic equations, including factoring, square root method, completing the square, and the quadratic formula. It also covers solving other types of equations that are quadratic in form, such as radical equations, through transformations. The objectives are to solve quadratic, radical, and other equations that are quadratic in form and to find sums and products of roots, the quadratic equation given roots, and solve application problems involving these equation types.

1. QUADRATIC EQUATIONS MATH10 ALGEBRAQuadratic Equations (Algebra and Trigonometry, Young 2nd Edition, page 113-135)

2. Week 3 Day 3GENERAL OBJECTIVEAt the end of the chapter the students are expected to:Solve quadratic equations using different methods,

3. Solve equations in quadratic form,

4. Solve equations leading to quadratic equation, and

5. Solve real-world problems that involve quadratic equation.Week 3 Day 3TODAY’S OBJECTIVEAt the end of the lesson the students are expected to: To distinguish between pure quadratic equation and complete quadratic equation,

6. To determine the number and type of solutions or roots of a quadratic equation based on the discriminant,

7. To define complex numbers, and

8. To solve quadratic equations by factoring, square root method, completing the square and quadratic formula. Week 3 Day 3DEFINITIONQUADRATIC EQUATIONA quadratic equation in x is an equation that can be written in the standard form where a, b, and c are real numbers and a  0 .a represents the numerical coefficient of x2 , b represents the numerical coefficient of x, and c represents the constant numerical term. Example:

9. Week 3 Day 3Pure Quadratic EquationIf b=0, then the quadratic equation is termed a "pure" quadratic equation. Example: 3x2 +6=0 Complete Quadratic EquationIf the equation contains both an x and x2 term, then it is a "complete" quadratic equation. The numerical coefficient c may or may not be zero in a complete quadratic equation. Example: x2 +5x+6=0 and 2x2 - 5x = 0

10. Week 3 Day 3DEFINITIONDISCRIMINANT OF A QUADRATIC EQUATIONThe term inside the radical, b2 -4ac, is called the discriminant.The discriminant gives important information about the corresponding solutions or roots of where a, b, and c are real numbers and a  0 .PositiveTwo distinct real rootsOne real root (a double or repeated root)ZeroNegativeTwo complex roots(complex conjugates)

11. Week 3 Day 3EXAMPLEDetermine the nature of roots of the following quadratic equation.

12. Week 3 Day 3DEFINITIONCOMPLEX NUMBER A complex number is an expression of the form where a and b are real numbers and a is the real part and b is the imaginary part .EXAMPLE3406-70-7

13. Week 3 Day 3SOLVING QUADRATIC EQUATIONSThere are four algebraic methods of solving quadratic equation in one variable, namely: solution by factoring

14. solution by square root method

15. solution by completing the square

16. solution by quadratic formulaWeek 3 Day 3SOLVING QUADRATIC EQUATIONS BY FACTORINGThe Factoring Method applies the Zero Product Property whichstates that if the product of two ormore factors equals zero, then at least one of the factors equals zero. Thus if B·C=0, then B=0 or C=0 or both.STEPS:Write the equation in standard form ax2 + bx + c = 0.Factor the left side completely.Apply the Zero Product Property to find the solution set.

17. Week 3 Day 3EXAMPLESolve the following equations.

18. Week 3 Day 3SOLVING QUADRATIC EQUATIONS BY SQUARE ROOT METHODThe Square Root Property states that if an expression squared is equal to a constant , then the expression is equal to the positive or negative square root of the constant.

19. Week 3 Day 3EXAMPLESolve the following equations.

20. Week 3 Day 3SOLVING QUADRATIC EQUATIONS BY COMPLETING THE SQUARESTEPS:

21. Week 3 Day 3SOLVING QUADRATIC EQUATIONS BY COMPLETING THE SQUARE

22. Week 3 Day 3EXAMPLESolve the following equations.

23. Week 3 Day 3SOLVING QUADRATIC EQUATIONS BY QUADRATIC FORMULATHE QUADRATIC FORMULAThe roots of the quadratic equation ax2 + bx + c = 0, where a, b, and c are constants and a  0 are given by:

24. DERIVATION OF QUADRATIC FORMULA BY COMPLETING THE SQUAREConsider the most general quadratic equation: Solve by completing the square: Divide the equation by the leading coefficient a.2. Subtract from both sides.3. Subtract half of and add the result to both sides.4. Write the left side of the equation as a perfect square and the right side as a single fraction.

25. DERIVATION OF QUADRATIC FORMULA BY COMPLETING THE SQUARESolve using the square root method.6. Subtract from both sides and simplify the radical.7. Write as a single fraction.8. We have derived the quadratic formula.

26. Week 3 Day 3EXAMPLESolve the following equations using the quadratic formula.

27. Week 3 Day 3SUMMARY The four methods for solving quadratic equations are: 3. completing the square1. factoring 2. square root method4. quadratic formulaFactoring and the square root method are the quickest and easiest but cannot always be used.

28. Quadratic formula and completing the square work for all quadratic equations and can yield three types of solutions: two distinct real rootsone real root (repeated)or two complex roots (conjugates of each other)

29. Week 4 Day 1EQUATIONS IN QUADRATIC FORM(OTHER TYPES)

30. Week 4 Day 1CLASSWORK

31. TODAY’S OBJECTIVEWeek 4 Day 1At the end of the lesson the students are expected to:To find the sum and product of roots of a quadratic equation.

32. To find the quadratic equation given the roots.

33. To transform a difficult equation into a simpler linear or quadratic equation,

34. To recognize the need to check solutions when the transformation process may produce extraneous solutions,

35. To solve radical equations.Week 4 Day 1RECALL The four methods for solving quadratic equations are: 3. completing the square1. factoring 2. square root method4. quadratic formulaFactoring and the square root method are the quickest and easiest but cannot always be used.

36. Quadratic formula and completing the square work for all quadratic equations and can yield three types of solutions: two distinct real rootsone real root (repeated)or two complex roots (conjugates of each other)

37. SUM AND PRODUCT OF ROOTS Recall from the quadratic formula that when Week 4 Day 1

38. Week 4 Day 1SUM OF ROOTSSum of roots = r + s

39. Week 4 Day 1PRODUCT OF ROOTSProduct of roots = (r) (s)

40. Week 4 Day 1EXAMPLEDetermine the value of k that satisfies the given condition

41. Week 4 Day 1FINDING THE QUADRATIC EQUATION GIVEN THE ROOTS Example: Find the quadratic equations with the given roots.

42. Week 4 Day 1RADICAL EQUATIONSRadical Equations are equations in which the variable isinside aradical (that is square root, cube root, or higher root).

43. Week 4 Day 1RADICAL EQUATIONSSteps in solving radical equations:Isolate the term with a radical on one side.Raise both (entire)sides of the equation to the power that will eliminate this radical and simplify the equation.If a radical remains, repeat steps 1 and 2.Solve the resulting linear or quadratic equation.Check the solutions and eliminate any extraneous solutions.Note: When both sides of the equations are squared extraneous solutions can arise , thus checking is part of the solution.

44. EXAMPLEWeek 4 Day 1Solve the following equations.

45. Week 4 Day 1CATCH THE MISTAKE

46. SUMMARY Week 4 Day 1.

47. Steps in solving radical equations:Isolate the term with a radical on one side.Raise both (entire)sides of the equation to the power that will eliminate this radical and simplify the equation.If a radical remains, repeat steps 1 and 2.Solve the resulting linear or quadratic equation.Check the solutions and eliminate any extraneous solutions.

48. TODAY’S OBJECTIVEWeek 4 Day 2At the end of the lesson the students are expected to:To solve equations that are quadratic in form,

49. To realize that not all polynomial equations are factorable.

50. To solve equations that are factorable.Week 4 Day 2EQUATIONS QUADRATIC IN FORM: u-SUBSTITUTIONEquations that are higher order or that have fractional powers often can be transformed into quadratic equation by introducing a u-substitution, thus the equation is in quadratic form.Example:

51. Week 4 Day 2EQUATIONS QUADRATIC IN FORM: u-SUBSTITUTIONSteps in solving equations quadratic in form:Identify the substitution.Transform the equation into a quadratic equation.Apply the substitution to rewrite the solution in terms the original variable.Solve the resulting equation.Check the solution in the original equation.

52. EXAMPLEWeek 4 Day 2Solve the following equations.

53. Week 4 Day 2FACTORABLE EQUATIONS EQUATIONS WITH RATIONAL EXPONENTS BY FACTORING

54. POLYNOMIALEQUATION USING FACTORING BY GROUPINGWeek 4 Day 2SUMMARYRadical equations, equations quadratic in form, and factorable equations can often be solved by transforming them into simpler linear or quadratic equations. Radical Equations: Isolate the term containing a radical and raise it to the appropriate power that will eliminate the radical. If there is more than one radical, it does not matter which radical is isolated first. Raising radical equations to powers may cause extraneous solutions, so check each solutions.Equations quadratic in form: Identify the u-substitution that transforms the equation into a quadratic equation. Solve the quadratic equation and then remember to transform back to the original equation.

55. Factorable equations: Look for a factor common to all terms or factor by grouping. APPLICATION PROBLEMS

56. Week 4 Day 3StartRECALLARead and analyze the problemMake a diagram or sketch if possibleSolve the equationDetermine the unknown quantity. Check the solution Set up an equation, assign variables to represent what you are asked to find.noIs the unknown solved?noyesyesDid you set up the equation?AEnd

57. Week 4 Day 3APPLICATION PROBLEMS1. If a person drops a water balloon off the rooftop of an 81 foot building, the height of the water balloon is given by the equation where t is in seconds. When will the water balloon hit the ground?(Classroom example 1.3.12 page 122)You have a rectangular box in which you can place a 7 foot long fishing rod perfectly on the diagonal. If the length of the box is 6 feet, how wide is that box?(Classroom example 1.3.13 page 123)3. A base ball diamond is a square. The distance from base to base is 90 feet. What is the distance from the home plate to the second base? (#108 page 125)

58. Week 4 Day 34. Lindsay andKimmie, working together, can balance the financials for the Kappa Kappa Gama sorority in 6days. Lindsay by herself can complete the job in 5days less than Kimmie. How long will it take Lindsay to complete the job by herself? (# 113 page 125)5.A rectangular piece of cardboard whose length is twice its width is used to construct an open box. Cutting a I foot by 1 foot square off of each corner and folding up the edges will yield an open box. If the desired volume is 12 cubic feet, what are the dimensions of the original piece of cardboard? (# 110 page 125)6.Aspeed boat takes 1 hour longer to go 24 miles up a river than to return. If the boat cruises at 10mph in still water, what is the rate of the current? (#140 page 126)

59. Week 4 Day 37.Cost for health insurance with a private policy is given by where C is the cost per day and a is the insured’s age in years. Health insurance for a six year old, a=6, is $4 a day (or $1,460 per year). At what age would someone be paying $9 a day (or $3,285 per year).(#73 page 134)8. The period (T) of a pendulum is related to the length (L) of the pendulum and acceleration due to gravity (g) by the formula . If the gravity is and the period is 1 second find the approximate length of the pendulum. Round to the nearest inch. (#80 page 134)

60. Week 4 Day 3HOMEWORK #s 8,31,44,53,56,66, 68,72,83,84,102, 104,106,114, 118,142 page124-127 #s 28, 50,72 page 133