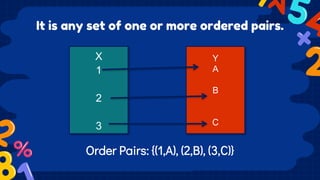
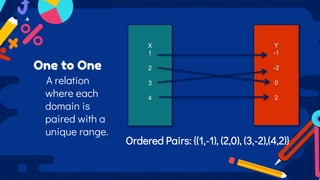
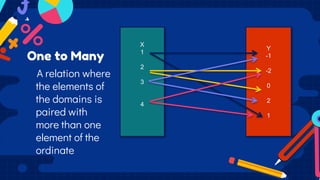
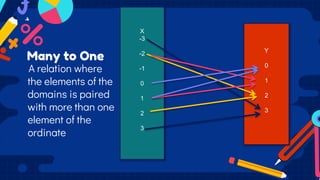
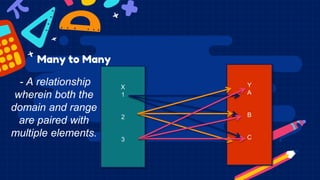
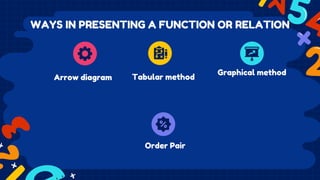
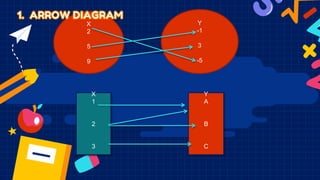
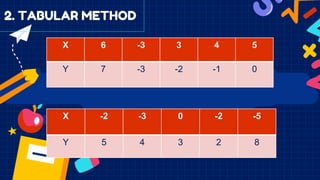
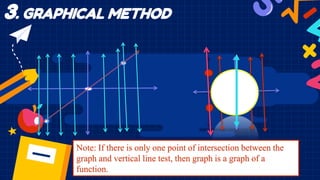
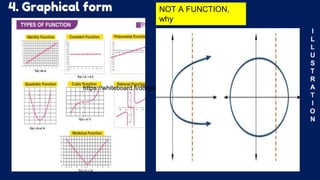
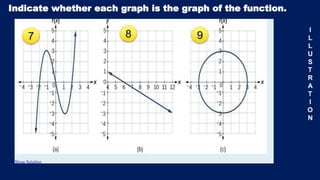
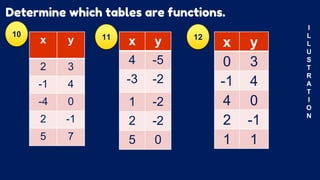
This document discusses functions and relations. It defines a relation as a set of ordered pairs and provides examples. It then defines a function as a special type of relation where each element of the domain corresponds to exactly one element of the range, meaning no two ordered pairs can have the same first element. The document discusses different types of relations including one-to-one, one-to-many, many-to-one, and many-to-many. It also discusses how functions can be presented using arrow diagrams, tables, graphs, and ordered pairs. Finally, it discusses function notation and evaluating functions by substituting values into the function.

1. Function and
Relation
Prepared by: Engr. Nora G. Yulo, BSChE , MS in Math, LPT

2. RELATION
01

3. It is any set of one or more ordered pairs.
X
1
2
3
Y
A
B
C
Order Pairs: {(1,A), (2,B), (3,C)}

4. 1. Relation – is a set of ordered pairs (x, y).
Examples:
1. A = {(0, 1), (1,2), (2, 3), (3, 4)}
2. B = {(STEM, Engineering), (ABM, Business Economics),
(HUMSS, AB Philosophy), (GAS, BS Education)}

5. Ordered Pairs: {(1,A), (2,B), (3,C)}
Range
Is the set of all
abscissa in a
relation
D: ( 1 , 2 , 3)
Is the set of all
ordinate in a
relation.
R: ( A , B , C)
Domain

6. KINDS OF RELATION
One to One One to Many Many to One
Many to
Many
A relation where
each domain is
paired with a
unique range.
A relation where
the elements of
the domains is
paired with more
than one element
of the ordinate
A relation
wherein more
than one
element of the
domain are
paired to an
element of the
range.
A relationship
wherein both the
domain and
range are paired
with multiple
elements.

7. One to One
A relation
where each
domain is
paired with a
unique range.
X
1
2
3
4
Y
-1
-2
0
2
Ordered Pairs: {(1,-1), (2,0), (3,-2),(4,2)}

8. One to Many
A relation where
the elements of
the domains is
paired with
more than one
element of the
ordinate
X
1
2
3
4
Y
-1
-2
0
2
1

9. Many to One
A relation where
the elements of the
domains is paired
with more than one
element of the
ordinate
X
-3
-2
-1
0
1
2
3
Y
0
1
2
3

10. Many to Many
- A relationship
wherein both the
domain and range
are paired with
multiple elements.
X
1
2
3
Y
A
B
C

11. FUNCTION 02
In mathematics, a function is a set of inputs with a
single output in each case.
Every function has a domain and range. The
domain is the set of independent values of the
variable x for a relation or a function is defined.
In simple words, the domain is a set of x-
values that generate the real values of y when
substituted in the function.

12. FUNCTIONS
- Is a correspondence between two sets
in which each element of the domain
corresponds to exactly one range.
- In other words, it may be described as a
special type of relation wherein no two
ordered pairs have the same abscissa.
What is a Function?
It is a relation in which repetition
of any element of its domain is not
allowed. Examples:
C = {(0, 0), (-1,1), (1, 1), (-2, 4), (2, 4)} is a function.
D = {(0, 0), (1, -1)), (1, 1), (4, -2), (4, 2)} is not a function.

13. WAYS IN PRESENTING A FUNCTION OR RELATION
Arrow diagram Tabular method
Graphical method
Order Pair

14. X
2
5
9
Y
-1
3
-5
X
1
2
3
Y
A
B
C

15. 2. TABULAR METHOD
X 6 -3 3 4 5
Y 7 -3 -2 -1 0
X -2 -3 0 -2 -5
Y 5 4 3 2 8

16. 3. GRAPHICAL METHOD
Note: If there is only one point of intersection between the
graph and vertical line test, then graph is a graph of a
function.

17. 4. Graphical form NOT A FUNCTION,
why
https://whiteboard.fi/d83ye

18. 4. ORDERED PAIRS
I = { ( -1 , 2) , (0, 4) , (1 , 6) }
A = { -2,4) , (6,3) , (2,2) , (2, 5) }
N = { -1 ,6 ) , ( -2 , 4) , (-4 , 4) , (2 , -6) }

19. Its your
time to
practice…
Write F if function and NF in not a
function

20. Determine which of the equation define a function or not.
1. Y - x² = 1
2. y² - x = 1
3. x³- y = 2
4. x² - y² = 1
5. Y =
𝟐𝒙 −𝒂
𝒙 −𝟏
6. Y = 4³ˣˉ¹

21. Indicate whether each graph is the graph of the function.
7 8 9

22. Determine which tables are functions.
x y
4 -5
-3 -2
1 -2
2 -2
5 0
x y
2 3
-1 4
-4 0
2 -1
5 7
x y
0 3
-1 4
4 0
2 -1
1 1
10 11 12

23. Indicate whether each graph is the graph of the function
13
14
15
16
17
18

24. FUNCTION NOTATI0N
● The most frequently used function notation is f(x) which is read as “f” of
“x”. In this case, the letter x, placed within the parentheses and the entire
symbol f(x), stand for the domain set and range set respectively.

25. Evaluation of Function
Note: Substitute all x`s of the given function by the given numerical value.
Apply the PEMDAS then simplify.
Given:
1. Find the numerical value of 𝑓 𝑥 = −2𝑥 + 9 𝑎𝑡 𝑓 3 .
2. Find the numerical value of 𝑓 𝑥 = 𝑥2
− 3𝑥 − 4 𝑎𝑡 𝑓 −1 𝑎𝑛𝑑 𝑓
1
2
.

26. Find the numerical value of 𝑓 𝑥 = −2𝑥 + 9 𝑎𝑡 𝑓 3 .

27. 2. Find the numerical value of 𝒇 𝒙 = 𝒙𝟐 − 𝟑𝒙 − 𝟒
𝒂𝒕 𝒇 −𝟏 .
Find the numerical value of 𝒇 𝒙 = 𝒙𝟐
− 𝟑𝒙 − 𝟒 𝒂𝒕 𝒇 −𝟏/𝟐 .

28. 3. Let g(x)=3x²+7x.
Evaluate a. g(4) b. -2 c. 0 d. ½ e. 2a

29. 3. Let g(x)=3x²+7x.
Evaluate a. g(4) b. -2 c. 0 d. ½ e. 2a

30. 3. Let g(x)=3x²+7x.
Evaluate a. g(4) b. -2 c. 0 d. ½ e. 2a

31. THANK YOU
AND
GODBLESS