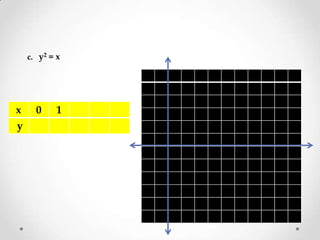
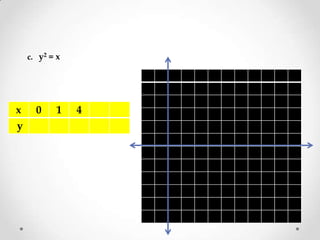
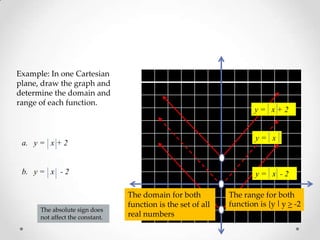
The document discusses different types of functions and their graphs. It provides examples of constant functions, linear functions, quadratic functions, and absolute value functions. It shows how to graph each type of function by plotting points and describes their domains and ranges. For linear functions, the domain is all real numbers and the range is also all real numbers. For quadratic functions, the graph is a parabola and the range only includes positive values. Absolute value functions have a domain of all real numbers and a range that is positive and excludes negative values below the constant.

1. GRAPH OF
FUNCTIONS

2. • A relation can be described as a graph
a. A = {(-5, -5), (-3, -3), (-1, -1), (1, 1),(3, 3), (5, 5)}
Since the domain is limited to
the set D = {-5, -3, -1, 1, 3, 5} ,
points should not be connected

3. An Equation can also be described as a graph
b. y = 2x + 1
x
y
-2
-1
0
1
2

4. An Equation can also be described as a graph
b. y = 2x + 1
x
y
-2
-3
-1
0
1
2

5. An Equation can also be described as a graph
b. y = 2x + 1
x
y
-2
-3
-1
-1
0
1
2

6. An Equation can also be described as a graph
b. y = 2x + 1
x
y
-2
-3
-1
-1
0
1
1
2

7. An Equation can also be described as a graph
b. y = 2x + 1
x
y
-2
-3
-1
-1
0
1
1
3
2

8. An Equation can also be described as a graph
b. y = 2x + 1
x
y
-2
-3
-1
-1
0
1
1
3
2
5

9. An Equation can also be described as a graph
b. y = 2x + 1
x
y
-2
-3
-1
-1
0
1
1
3
No domain is specified
when a function is
defined
2
5

10. c. y2 = x
x
y
0

11. c. y2 = x
x
y
0
1

12. c. y2 = x
x
y
0
1
4

13. c. y2 = x
x
y
0
1
4
9

14. c. y2 = x
x
y
0
0
1
4
9
16

15. c. y2 = x
x
y
0
0
1
+1
4
9

16. c. y2 = x
x
y
0
0
1 4
+1 +2
9

17. c. y2 = x
x
y
0
0
1 4 9
+1 +2 +3

18. c. y2 = x
x
y
0
0
1 4 9
+1 +2 +3
The domain of this kind
of relation is { x x > 0 }

19. The Vertical Line Test
• A graph of a relation is a function if any vertical line
drawn passing through the graph intersects it at
exactly one point.
 Determine which of the following graphs of relation represents a
function.

20. • Constant Functions

A constant function C consists of a single real number k in its range for
all real numbers x in its domain.

21. IDENTITY
FUNCTION
I(x) = x
If the domain is specified to be the set of
all real numbers, the range of the identity
function is also the set of all real numbers

22. • Some points on the graph of an I(x) = x are
(-2, -2), (-1, -1), (0, 0),(1, 1), (2, 2)

23. POLYNOMIAL
FUNCTIONS
A constant function is a polynomial function
of the degree 0. If a polynomial function is of
the first degree, then it is called a linear
function

24. Polynomial Functions:
Linear Function
f (x) = mx + b
Note: f(x) = y

25. • Draw the graph of a linear function
f(x) = -2x + 5
x
f(x
)
-1
0
1
2
3

26. • Draw the graph of a linear function
f(x) = -2x + 5
x
-1
f(x
)
7
0
1
2
3

27. • Draw the graph of a linear function
f(x) = -2x + 5
x
-1
0
f(x
)
7
5
1
2
3

28. • Draw the graph of a linear function
f(x) = -2x + 5
x
-1
0
1
f(x
)
7
5
3
2
3

29. • Draw the graph of a linear function
f(x) = -2x + 5
x
-1
0
1
2
f(x
)
7
5
3
1
3

30. • Draw the graph of a linear function
f(x) = -2x + 5
x
-1
0
1
2
3
f(x
)
7
5
3
1
-1
The domain is x x is
a real number and it
follows that the range
is y y is a real number

31. If a polynomial function is of the second
degree, then it is called a quadratic
function

32. Polynomial Functions:
Quadratic Function
f (x) = ax2 + bx + c

33. • Draw the graph of the quadratic equation
g(x) = x2
x
g(x
)
-2
-1
0
1
2

34. • Draw the graph of the quadratic equation
g(x) = x2
x
-2
g(x
)
4
-1
0
1
2

35. • Draw the graph of the quadratic equation
g(x) = x2
x
-2
-1
g(x
)
4
1
0
1
2

36. • Draw the graph of the quadratic equation
g(x) = x2
x
-2
-1
0
g(x
)
4
1
0
1
2

37. • Draw the graph of the quadratic equation
g(x) = x2
x
-2
-1
0
1
g(x
)
4
1
0
1
2

38. • Draw the graph of the quadratic equation
g(x) = x2
x
-2
-1
0
1
2
g(x
)
4
1
0
1
4
A quadratic function
is a parabola.
The range for both
function is {y ǀ y > 0
}

39. Absolute Value Functions:
f (x) = x

40. The domain of an absolute
value function is the set of real
numbers and the range is {f(x)
f(x) > 0 }

41. Example: In one Cartesian
plane, draw the graph and
determine the domain and
range of each function.
y= x
a. y = x + 2
Simply shift to the
left
b. y = x - 2
Simply shift to the
right
y= x+2
The domain for both
function is the set of all
real numbers
y= x-2
The range for both
function is {y ǀ y > 0
}

42. Example: In one Cartesian
plane, draw the graph and
determine the domain and
range of each function.
y= x+2
y= x
a. y = x + 2
b. y = x - 2
The absolute sign does
not affect the constant.
y= x -2
The domain for both
function is the set of all
real numbers
The range for both
function is {y ǀ y > -2
}

43. • Draw the graph of each function. Determine its
domain and range.
1. y = 7
6. y = 3x – 1
2. y = -5
7. y = 2x2
3. y = 2x + 3
8.
4. y = ǀ x + 3 ǀ
9. y = ǀ x – 3 ǀ
5. y = ǀxǀ - 4
y = x2 + 2
10. y = ǀxǀ + 4