Embed presentation
Downloaded 21 times









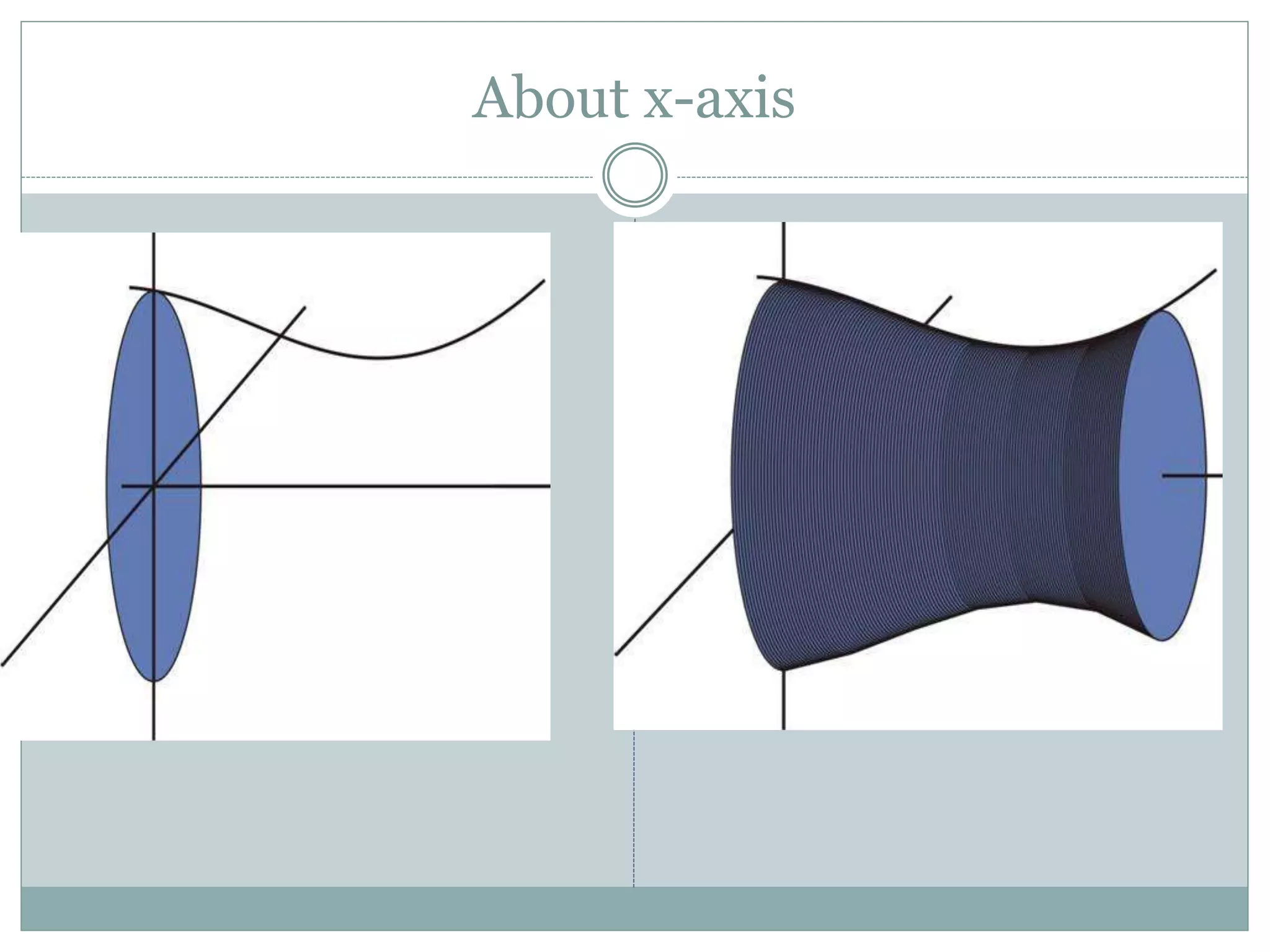
![Example 2: (pg: 425)
Find the volume of the
solid that is obtained
when the region under
the curve
over the interval [1, 4]
is revolved about the x-
axis.
xxfy )(](https://image.slidesharecdn.com/6-160721084500/75/6-2-volume-of-solid-of-revolution-15-2048.jpg)
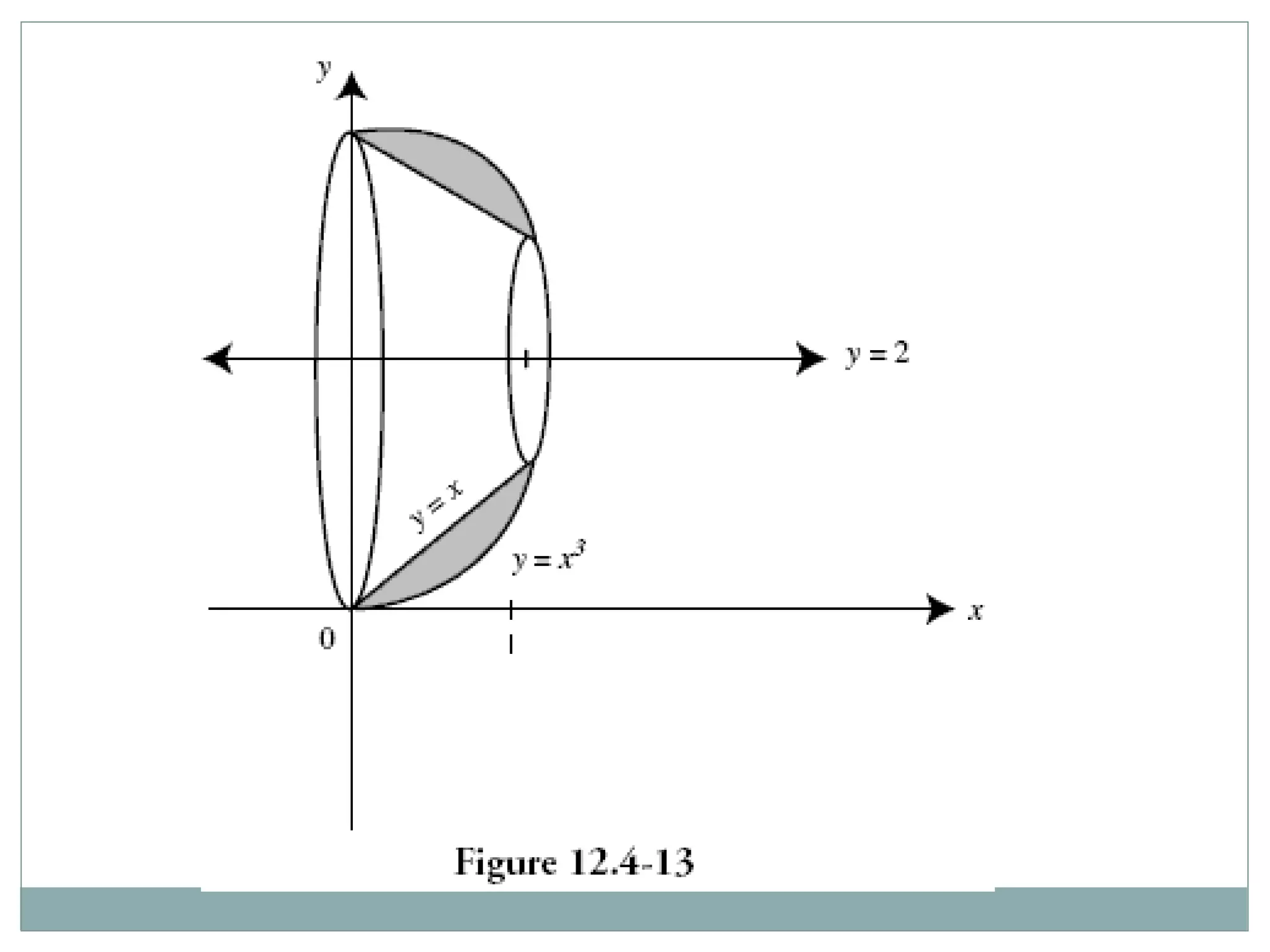
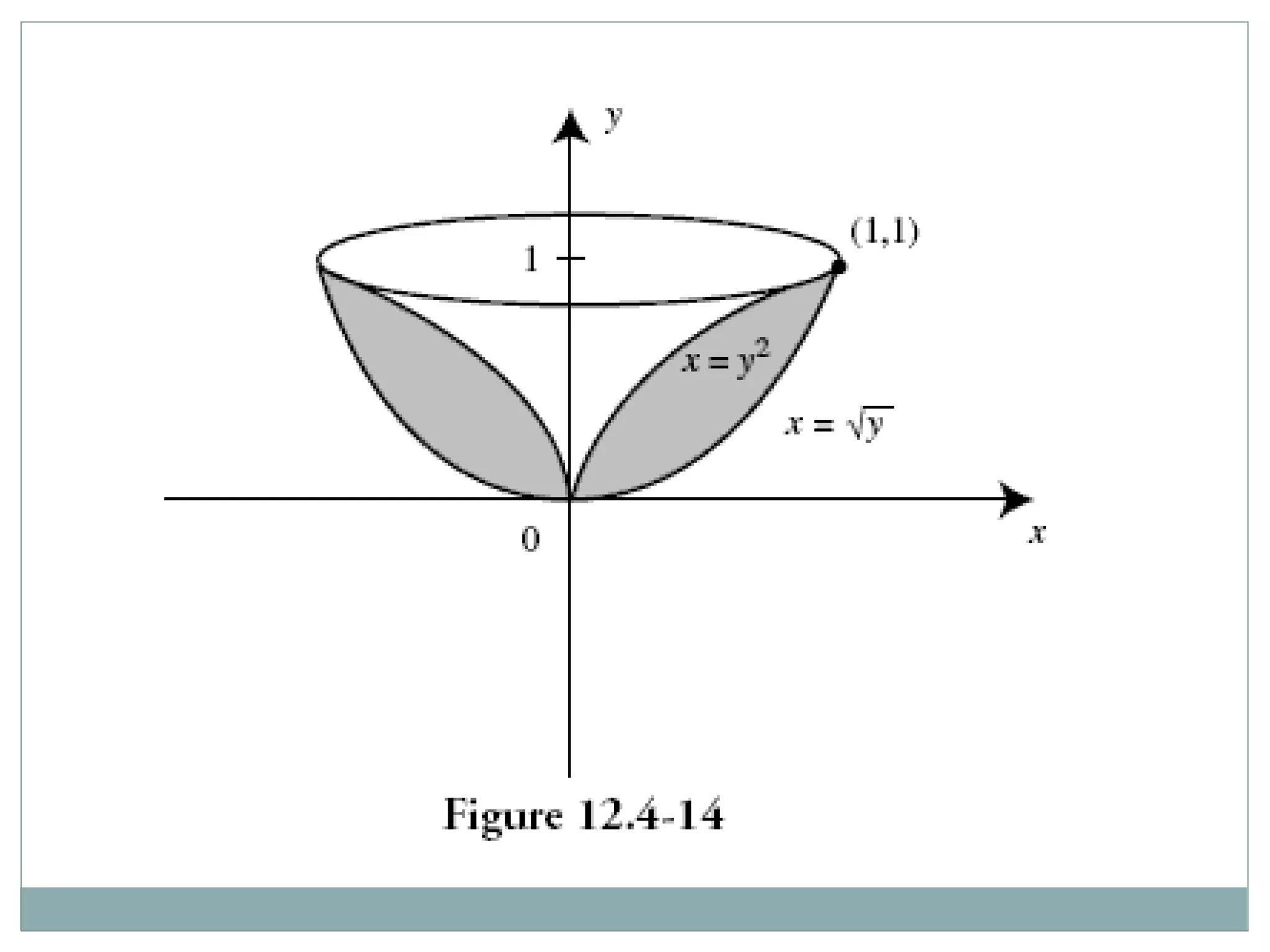
![11–18 Find the volume of the solid that results when the
region
enclosed by the given curves is revolved about the x-
axis. "
11. y = '25 − x2, y = 3
12. y = 9 − x2, y = 0
13. x = 'y, x = y/4
14. y = sin x, y = cos x, x = 0, x = "/4
[Hint: Use the identity cos 2x = cos2 x − sin2 x.]
15. y = ex, y = 0, x = 0, x = ln 3
16. y = e−2x, y = 0, x = 0, x = 1
17. y =1'4 + x2
, x = −2, x = 2, y = 0
18. y =
e3x
'1 + e6x
, x = 0, x = 1, y = 0](https://image.slidesharecdn.com/6-160721084500/75/6-2-volume-of-solid-of-revolution-16-2048.jpg)




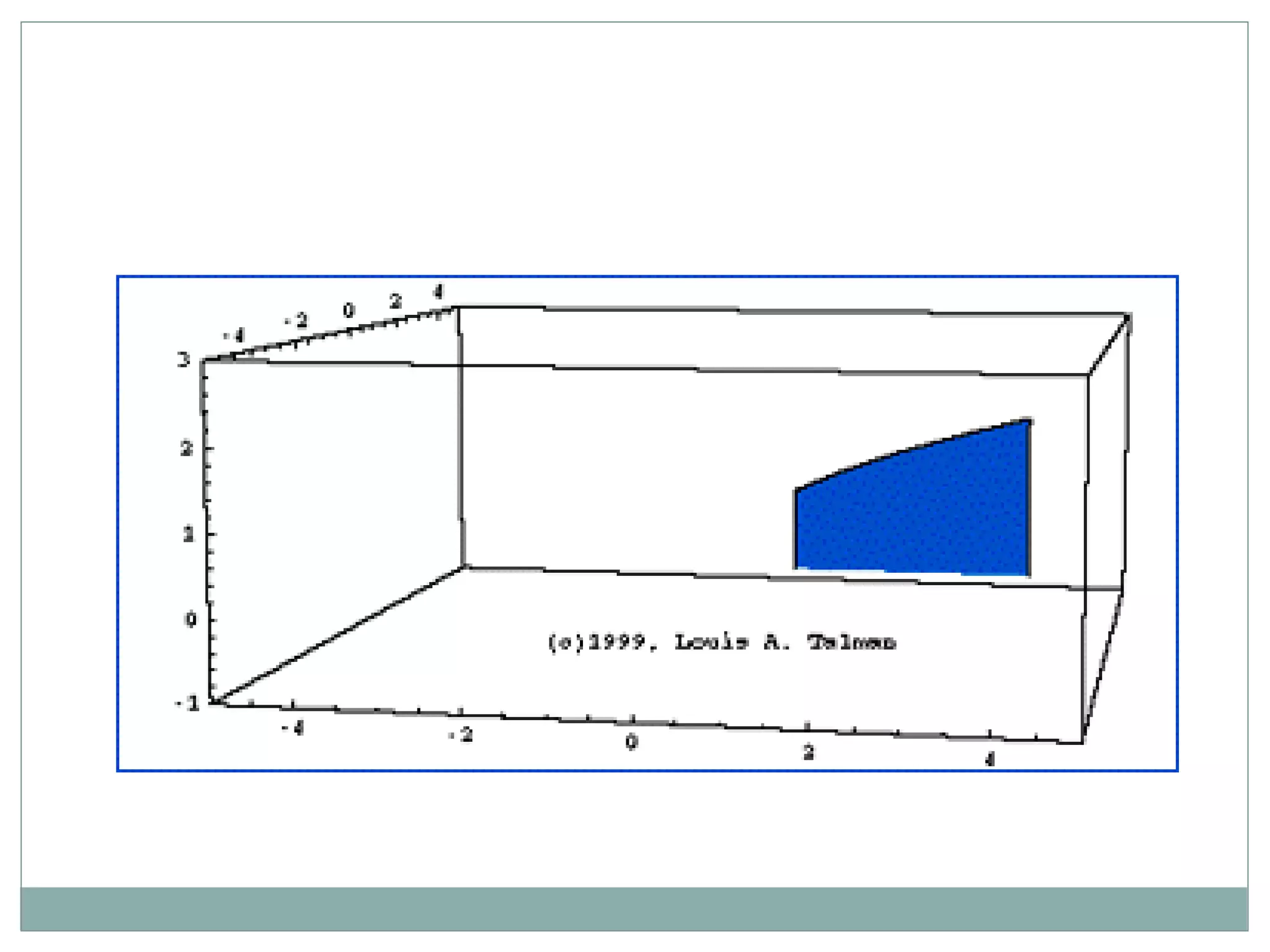


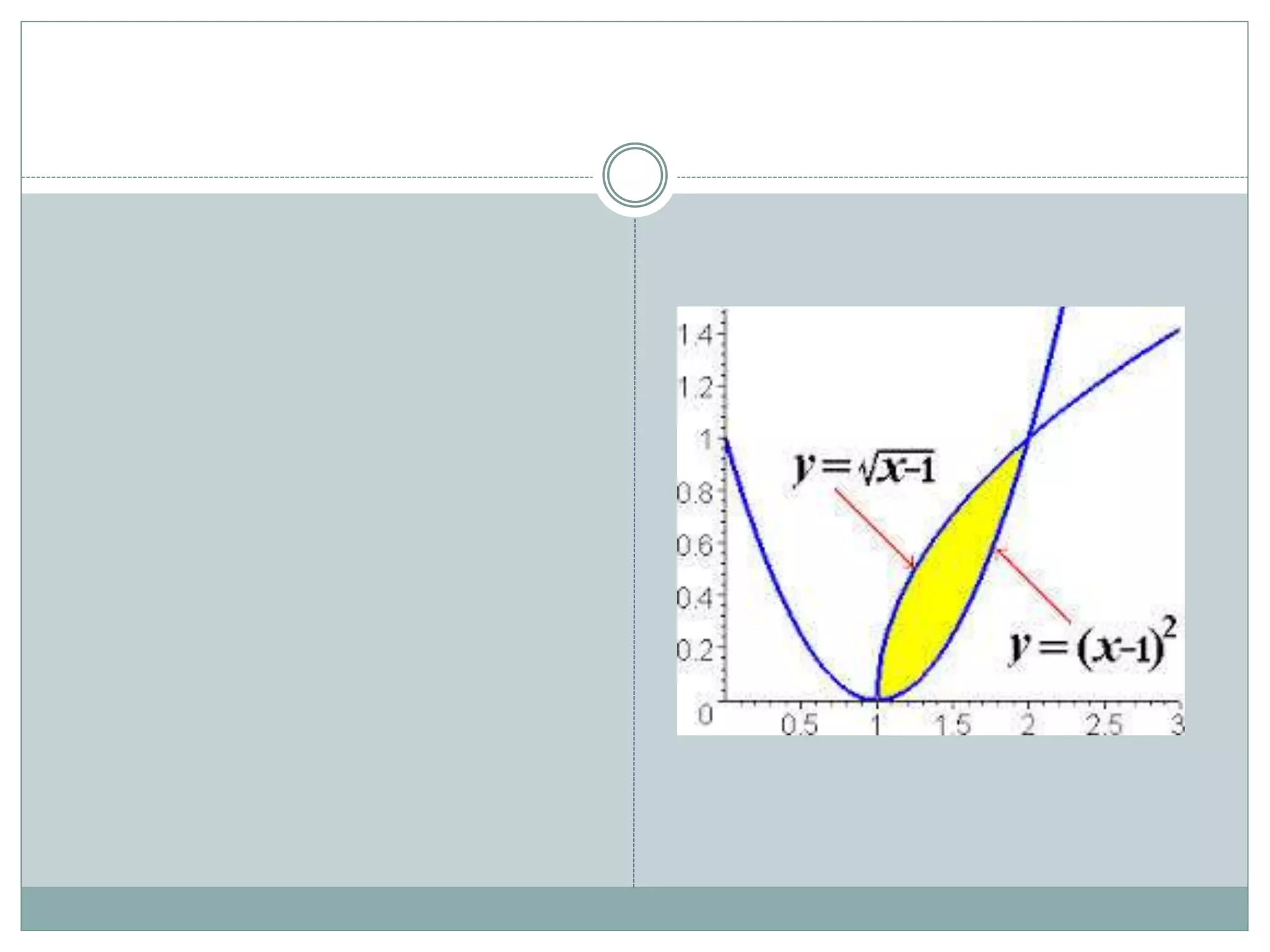
![Example 4: (pg: 426)
Find the volume of the
solid generated when
the region between the
graphs of the equations
and g(x)=x over the
interval [0, 2] is
revolved about the x-
axis.
2
2
1
)( xxf ](https://image.slidesharecdn.com/6-160721084500/75/6-2-volume-of-solid-of-revolution-24-2048.jpg)







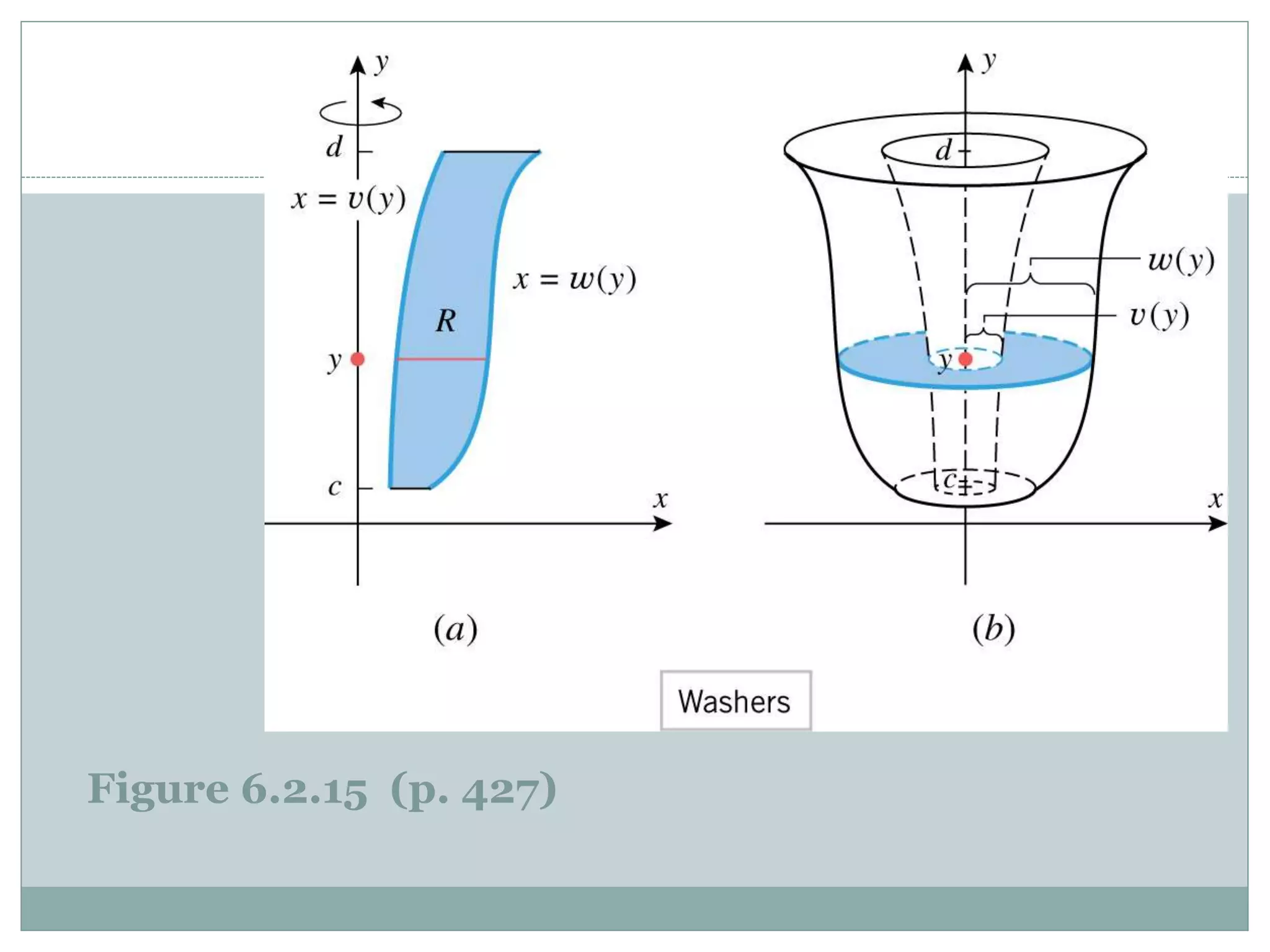


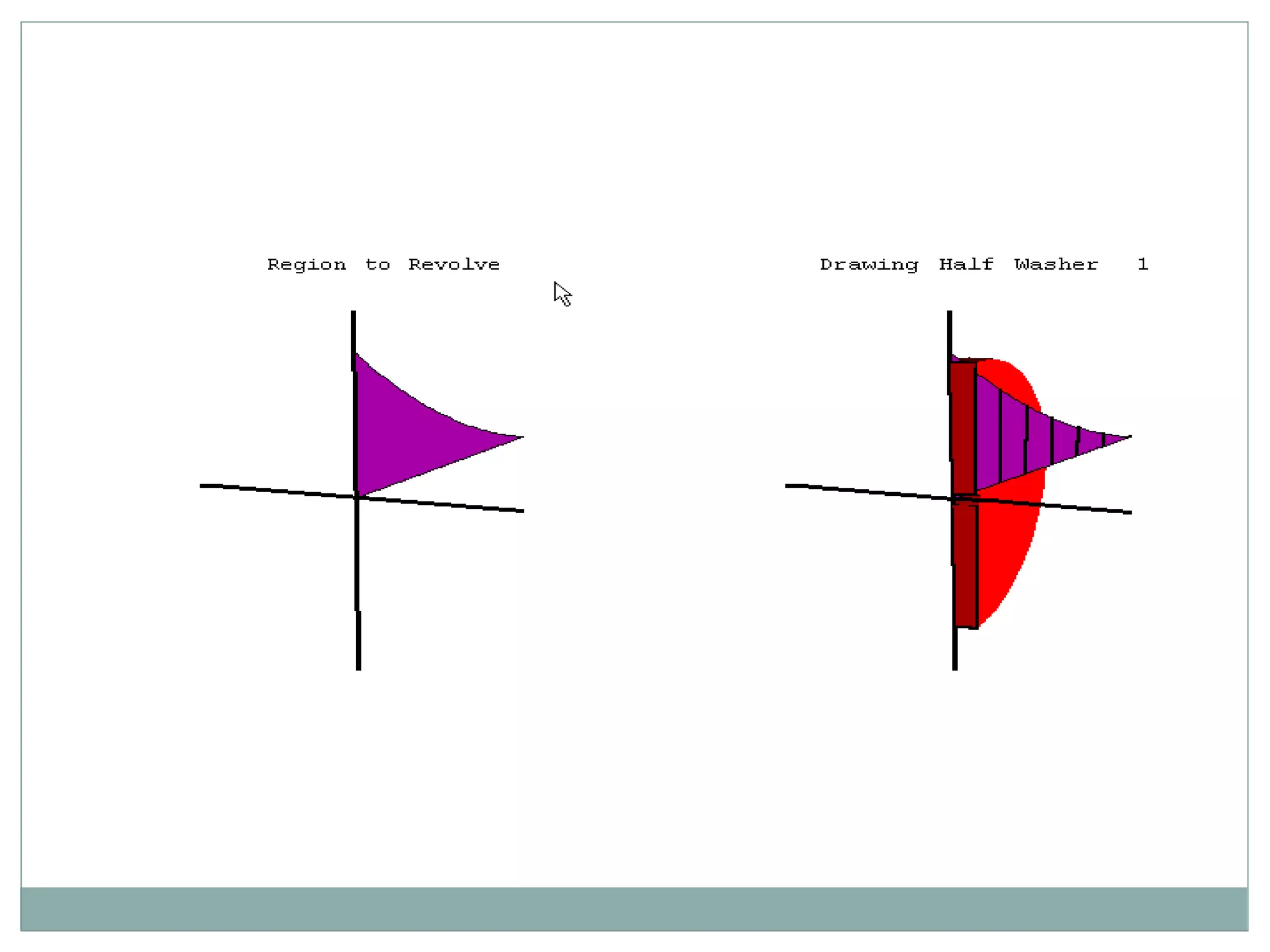




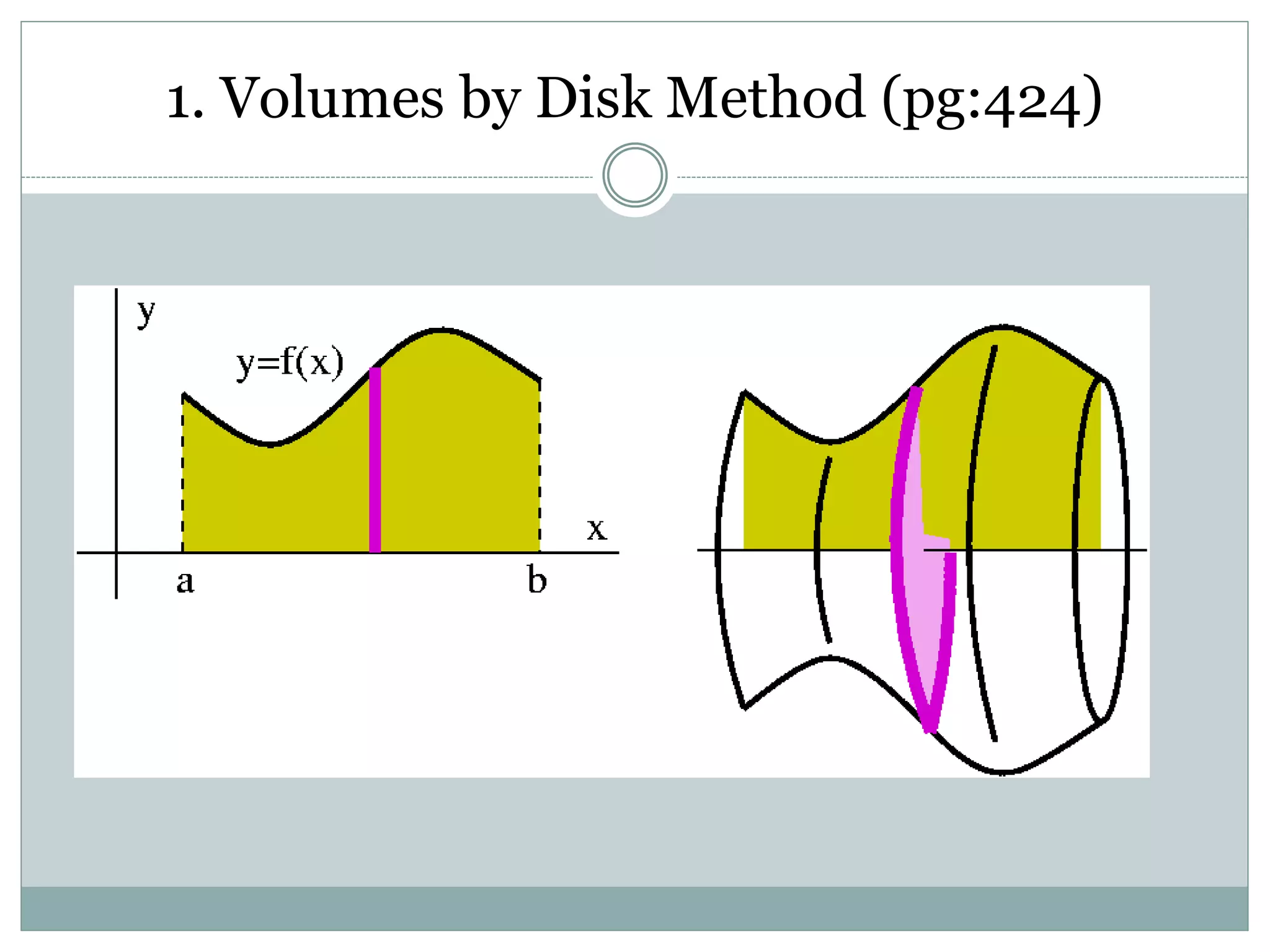
1. The document discusses different methods for calculating the volume of solids obtained by revolving a region about an axis, including the disk method, washer method, and examples applying each method. 2. The disk method is used when the region is revolved about the x-axis, and the washer method is used when the region is revolved about the y-axis. 3. Examples are provided to demonstrate calculating the volume of solids generated by revolving regions between curves over intervals about the x-axis and y-axis.














![Example 2: (pg: 425)
Find the volume of the
solid that is obtained
when the region under
the curve
over the interval [1, 4]
is revolved about the x-
axis.
xxfy )(](https://image.slidesharecdn.com/6-160721084500/75/6-2-volume-of-solid-of-revolution-15-2048.jpg)
![11–18 Find the volume of the solid that results when the
region
enclosed by the given curves is revolved about the x-
axis. "
11. y = '25 − x2, y = 3
12. y = 9 − x2, y = 0
13. x = 'y, x = y/4
14. y = sin x, y = cos x, x = 0, x = "/4
[Hint: Use the identity cos 2x = cos2 x − sin2 x.]
15. y = ex, y = 0, x = 0, x = ln 3
16. y = e−2x, y = 0, x = 0, x = 1
17. y =1'4 + x2
, x = −2, x = 2, y = 0
18. y =
e3x
'1 + e6x
, x = 0, x = 1, y = 0](https://image.slidesharecdn.com/6-160721084500/75/6-2-volume-of-solid-of-revolution-16-2048.jpg)







![Example 4: (pg: 426)
Find the volume of the
solid generated when
the region between the
graphs of the equations
and g(x)=x over the
interval [0, 2] is
revolved about the x-
axis.
2
2
1
)( xxf ](https://image.slidesharecdn.com/6-160721084500/75/6-2-volume-of-solid-of-revolution-24-2048.jpg)

















