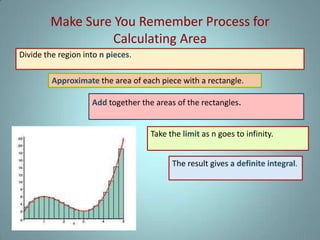
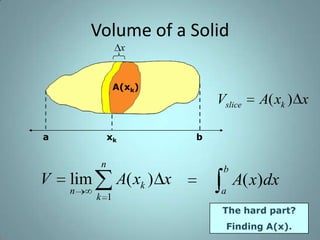
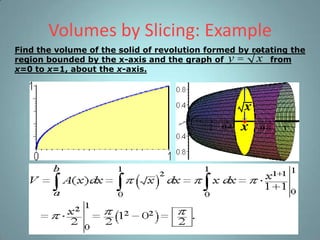
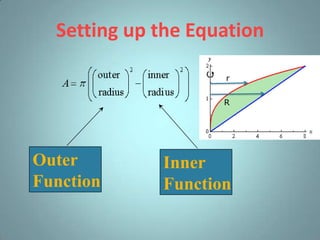
This document provides information about calculating volumes of solids of revolution using integral calculus. It discusses the disk method and washer method for setting up integrals to solve for volumes. Examples are provided for finding the volume of a solid rotated about the x-axis using each method. Students are reminded of the definition of a definite integral and the process for calculating areas. Helpful links and sources are listed at the end.

1. AP CALCULUS
Mrs. DiCosmo
Volumes of Solids of Revolution:
• Disk Method
• Washer Method

3. You will be able to calculate volumes
of irregular shaped solids

4. Some of the Professional fields that
are using this particular concepts of
Integral Calculus
MRI & CAT
scan
Construction
Idustrial
Designs
Containers
and Packaging

5. Reminder !!!!!!!!
Definition of a Definite Integral
n
lim
n
f ( xk ) x
k 1
x
xk
b a
n
a k x
b
a
f ( x)dx

6. Make Sure You Remember Process for
Calculating Area
Divide the region into n pieces.
Approximate the area of each piece with a rectangle.
Add together the areas of the rectangles.
Take the limit as n goes to infinity.
The result gives a definite integral.

7. General Idea - Slicing
1.
Divide the solid into n pieces (slices).
2.
Approximate the volume of each slice.
3.
Add together the volumes of the slices.
4.
Take the limit as n goes to infinity.
5.
The result gives a definite integral.

8. Disk Method

9. Volume of a Slice
Volume of a cylinder?
V
r
2
r h
What if the ends are
not circles?
V
A
h
Ah
What if the ends are not
perpendicular to the side?
No difference!
(note: h is the distance
between the ends)

10. Volume of a Solid
x
A(xk)
Vslice
a
xk
n
V
lim
n
A( xk ) x
k 1
A( xk ) x
b
b
a
A( x)dx
The hard part?
Finding A(x).

11. Volumes by Slicing: Example
Find the volume of the solid of revolution formed by rotating the
x from
region bounded by the x-axis and the graph of y =
x=0 to x=1, about the x-axis.

12. Here is a Problem for You:
Find the volume of the solid of revolution formed by rotating the
region bounded by the x-axis and the graph of y = x4, from x=1 to
x=2, about the x-axis.
Ready?
A(x) = p(x4)2= px8.

13. Washer Method

14. • Consider the area between two functions
rotated about the axis
• Now we have a hollow solid
• We will sum the volumes of washers

15. Setting up the Equation
r
R
Outer
Function
Inner
Function

16. Solids of Revolution
A solid obtained by revolving a region around a line.
When the axis of rotation is
NOT a border of the region.
f(x)
g(x)
Creates a “pipe” and the
slice will be a washer.
Find the volume of the solid
and subtract the volume of
the hole.
V
V
b
b
2
f ( x) dx
a
b
a
f ( x)
2
a
2
g ( x) dx
a
xk
b
2
g ( x) dx
NOTE: Cross-section is
perpendicular to the
axis of rotation.

17. Example:
Find the volume of the solid formed by revolving the
region bounded by y = (x) and y = x² over the interval [0,
1] about the x – axis.
b
([ f ( x)]2 [ g ( x)]2 )dx
V
a
1
V
2
x
x
2 2
0
V = p ò (x - x )dx
1
4
0
æx x ö
3
V =pç - ÷ =
è 2 5 ø 0 10
2
5
1
dx

18. Here is a Problem for You:
Ready?

19. So……how do you calculate
volumes of revolution?
• Graph your functions to create the region.
• Spin the region about the appropriate axis.
• Set up your integral.
• Integrate the function.
• Evaluate the integral.

20. ANY QUESTIONS ?

21. HOMEFUN !!!
Pg. 423 / ex. 3-13 all
Helpful Links:
http://www.learnerstv.com/Free-maths-Videolectures-ltv295-Page1.htm
https://www.khanacademy.org/math/calculus/integra
l-calculus

22. Sources:
http://www2.bc.cc.ca.us/resperic/Math6A/
Lectures/ch6/2/washer.htm
http://tutorial.math.lamar.edu/Classes/Cal
cI/VolumeWithRings.aspx
http://math.hws.edu/~mitchell/Math131S1
3/tufte-latex/Volume2.pdf
https://www.google.com
http://www.learnerstv.com/Free
-maths-Video-lectures-ltv295Page1.htm
https://www.khanacademy.org/
math/calculus/integral-calculus

23. Assessment