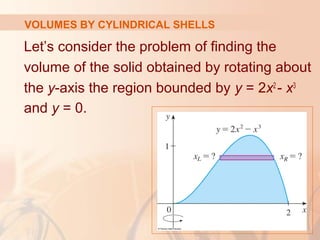
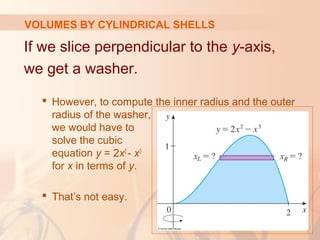
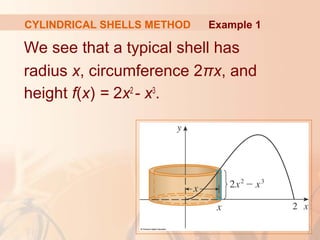
This document discusses using the method of cylindrical shells to calculate volumes of solids of revolution. It provides an example calculating the volume of the solid obtained by rotating the region between the curves y=2x^2 - x^3 and y=0 about the y-axis. The method involves imagining the solid as being composed of cylindrical shells and using the formula V=2π∫_{a}^{b} x*f(x) dx to calculate the volume, where f(x) is the height of each shell.









![The equation can be remembered as:
V = [circumference] [height] [thickness]
CYLINDRICAL SHELLS METHOD
2V rh rπ= ∆](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-12-320.jpg)
![Now, let S be the solid
obtained by rotating
about the y-axis the
region bounded by
y = f(x) [where f(x) ≥ 0],
y = 0, x = a and x = b,
where b > a ≥ 0.
CYLINDRICAL SHELLS METHOD](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-13-320.jpg)
![Divide the interval [a, b] into n subintervals
[xi - 1, xi ] of equal width and let be
the midpoint of the i th subinterval.
x∆ix
CYLINDRICAL SHELLS METHOD](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-14-320.jpg)
![The rectangle with
base [xi - 1, xi ] and
height is rotated
about the y-axis.
The result is a
cylindrical shell with
average radius ,
height , and
thickness ∆x.
( )if x
( )if x
ix
CYLINDRICAL SHELLS METHOD](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-15-320.jpg)
![Thus, by Formula 1, its volume is
calculated as follows:
(2 )[ ( )]i i iV x f x xπ= ∆
CYLINDRICAL SHELLS METHOD](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-16-320.jpg)




![Here’s the best way to remember
the formula.
Think of a typical shell,
cut and flattened,
with radius x,
circumference 2πx,
height f(x), and
thickness ∆x or dx:
( ){
[ ] {2 ( )
b
a
thicknesscircumference height
x f x dxπ∫ 123
CYLINDRICAL SHELLS METHOD](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-21-320.jpg)


















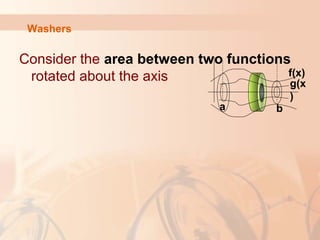
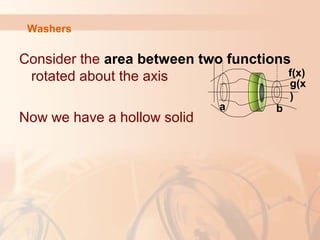

![Washers
f(x)
a b
g(x
)[ ] [ ]{ }2 2
( ) ( )
b
a
V f x g x dxπ= −∫
Outer
Function
Inner
Function](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-44-320.jpg)
![Find the volume of the solid formed by revolving the
region bounded by y = √(x) and y = x² over the interval
[0, 1] about the x – axis.](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-45-320.jpg)
![Find the volume of the solid formed by revolving the
region bounded by y = √(x) and y = x² over the interval
[0, 1] about the x – axis.
2 2
([ ( )] [ ( )] )
b
a
V f x g x dxπ= −∫](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-46-320.jpg)
![Find the volume of the solid formed by revolving the
region bounded by y = √(x) and y = x² over the interval
[0, 1] about the x – axis.
2 2
([ ( )] [ ( )] )
b
a
V f x g x dxπ= −∫
( ) ( )∫ −=
1
0
222
dxxxV π](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-47-320.jpg)
![Find the volume of the solid formed by revolving the
region bounded by y = √(x) and y = x² over the interval
[0, 1] about the x – axis.
2 2
([ ( )] [ ( )] )
b
a
V f x g x dxπ= −∫
( ) ( )∫ −=
1
0
222
dxxxV π
( )∫ −=
1
0
4
dxxxV π](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-48-320.jpg)
![Find the volume of the solid formed by revolving the
region bounded by y = √(x) and y = x² over the interval
[0, 1] about the x – axis.
2 2
([ ( )] [ ( )] )
b
a
V f x g x dxπ= −∫
( ) ( )∫ −=
1
0
222
dxxxV π
( )∫ −=
1
0
4
dxxxV π
1
0
52
5
1
2
1
−= xxV π](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-49-320.jpg)
![Find the volume of the solid formed by revolving the
region bounded by y = √(x) and y = x² over the interval
[0, 1] about the x – axis.
2 2
([ ( )] [ ( )] )
b
a
V f x g x dxπ= −∫
( ) ( )∫ −=
1
0
222
dxxxV π
( )∫ −=
1
0
4
dxxxV π
1
0
52
5
1
2
1
−= xxV π
10
3π
=](https://image.slidesharecdn.com/1-160506152816/85/Application-of-integration-50-320.jpg)