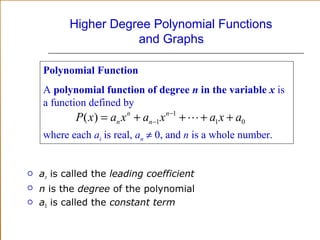
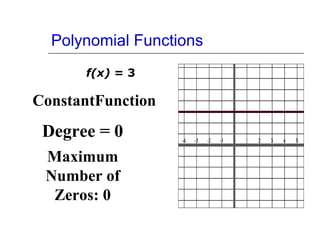
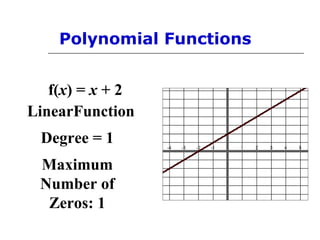
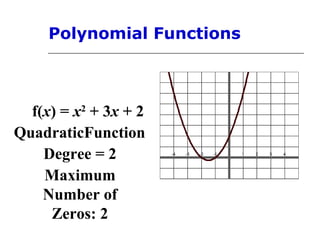
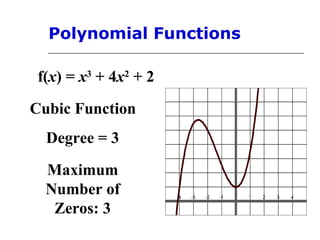
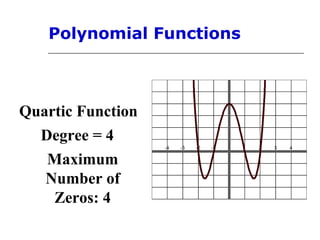
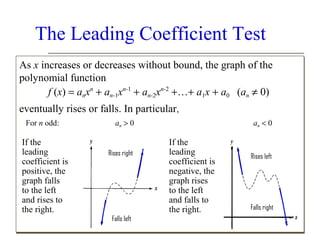
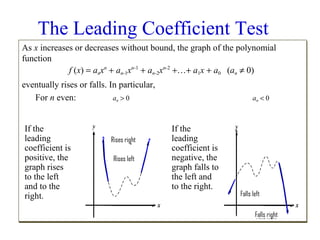
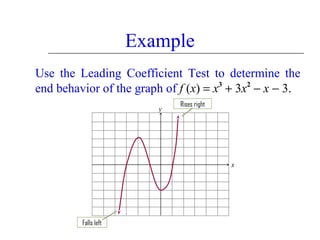
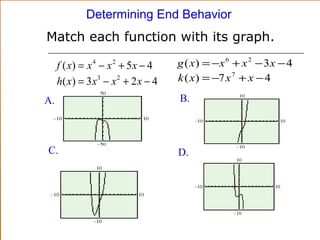
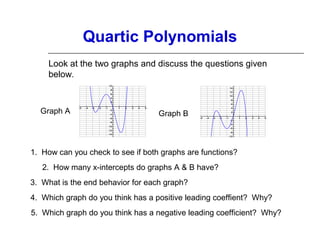
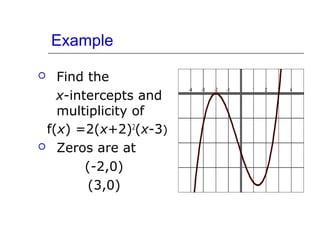
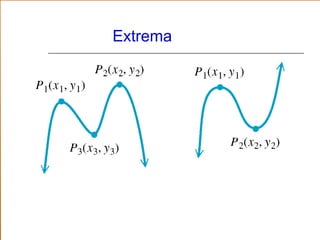
This document discusses polynomial functions and their graphs. It defines polynomial functions as functions of the form P(x) = anxn + an-1xn-1 + ... + a1x + a0, where an is the leading coefficient. The degree of the polynomial determines features of its graph like the maximum number of x-intercepts. The leading coefficient test determines the end behavior of the graph. Key features of polynomial graphs are intercepts, extrema, and end behavior.

1. Polynomial Functions and
Graphs

2. Higher Degree Polynomial Functions
and Graphs
Polynomial Function
A polynomial function of degree n in the variable x is
a function defined by
P( x) = an x + an−1 x
n
n −1
+  + a1 x + a0
where each ai is real, an ≠ 0, and n is a whole number.

an is called the leading coefficient

n is the degree of the polynomial
a0 is called the constant term


3. Polynomial Functions
Polynomial
Function in
General Form
y = ax + b
y = ax 2 + bx + c
y = ax 3 + bx 2 + cx + d
y = ax 4 + bx 3 + cx 2 + dx + e
Degree
Name of
Function
1
2
3
4
Linear
Quadratic
Cubic
Quartic
The largest exponent within the
polynomial determines the degree of the
polynomial.

4. Polynomial Functions
f(x) = 3
ConstantFunction
Degree = 0
Maximum
Number of
Zeros: 0

5. Polynomial Functions
f(x) = x + 2
LinearFunction
Degree = 1
Maximum
Number of
Zeros: 1

6. Polynomial Functions
f(x) = x2 + 3x + 2
QuadraticFunction
Degree = 2
Maximum
Number of
Zeros: 2

7. Polynomial Functions
f(x) = x3 + 4x2 + 2
Cubic Function
Degree = 3
Maximum
Number of
Zeros: 3

8. Polynomial Functions
Quartic Function
Degree = 4
Maximum
Number of
Zeros: 4

9. Leading Coefficient
The leading coefficient is the coefficient of
the first term in a polynomial when the
terms are written in descending order by
degrees.
For example, the quartic function
f(x) = -2x4 + x3 – 5x2 – 10 has a leading
coefficient of -2.

10. The Leading Coefficient Test
As x increases or decreases without bound, the graph of the
polynomial function
n
n-1
n-2
f (x) = anxn + an-1xn-1 + an-2xn-2 +…+ a1x + a0 (an ≠ 0)
n
n-1
n-2
1
0
n
eventually rises or falls. In particular,
For n odd:
If the
leading
coefficient is
positive, the
graph falls
to the left
and rises to
the right.
an > 0
n
Rises right
Falls left
an < 0
n
If the
leading
coefficient is
negative, the
graph rises
to the left
and falls to
the right.
Rises left
Falls right

11. The Leading Coefficient Test
As x increases or decreases without bound, the graph of the polynomial
function
n
n-1
n-2
f (x) = anxn + an-1xn-1 + an-2xn-2 +…+ a1x + a0 (an ≠ 0)
n
n-1
n-2
1
0
n
eventually rises or falls. In particular,
For n even:
an > 0
an < 0
n
n
If the
leading
coefficient is
positive, the
graph rises
to the left
and to the
right.
Rises right
Rises left
If the
leading
coefficient is
negative, the
graph falls to
the left and
to the right.
Falls left
Falls right

12. Example
Use the Leading Coefficient Test to determine the
end behavior of the graph of f (x) = x3 + 3x2 − x − 3.
y
Rises right
x
Falls left

13. Determining End Behavior
Match each function with its graph.
f ( x) = x − x + 5 x − 4
h( x ) = 3 x 3 − x 2 + 2 x − 4
4
A.
C.
2
g ( x ) = −x 6 + x 2 − 3 x − 4
k ( x ) = −7 x 7 + x − 4
B.
D.

14. Quartic Polynomials
Look at the two graphs and discuss the questions given
below.
10
14
8
12
6
10
4
8
2
Graph A
-5
-4
-3
-2
-1
-2
-4
-6
6
1
2
3
4
5
Graph B
4
2
-5
-4
-3
-8
-10
-12
-14
-2
-1
-2
1
2
3
4
5
-4
-6
-8
-10
1. How can you check to see if both graphs are functions?
2. How many x-intercepts do graphs A & B have?
3. What is the end behavior for each graph?
4. Which graph do you think has a positive leading coeffient? Why?
5. Which graph do you think has a negative leading coefficient? Why?

15. x-Intercepts (Real Zeros)
Number Of x-Intercepts of a Polynomial Function
A polynomial function of degree n will have a maximum
of n x- intercepts (real zeros).
Find all zeros of f (x) = -x4 + 4x3 - 4x2.
−x4 + 4x3 − 4x2 = 0
x4 − 4x3 + 4x2 = 0
x2(x2 − 4x + 4) = 0
x2(x − 2)2 = 0
x2 = 0
x=0
or
(x − 2)2 = 0
x=2
We now have a polynomial equation.
Multiply both sides by −1. (optional step)
Factor out x2.
Factor completely.
Set each factor equal to zero.
Solve for x.
(0,0)
(2,0)

16. Multiplicity and x-Intercepts
If r is a zero of even multiplicity, then
the graph touches the x-axis and
turns around at r. If r is a zero of
odd multiplicity, then the graph
crosses the x-axis at r. Regardless
of whether a zero is even or odd,
graphs tend to flatten out at zeros
with multiplicity greater than one.

17. Example
Find the
x-intercepts and
multiplicity of
f(x) =2(x+2)2(x-3)
 Zeros are at
(-2,0)
(3,0)


18. Extrema

Turning points – where the graph of a function changes from
increasing to decreasing or vice versa. The number of turning points
of the graph of a polynomial function of degree n ≥ 1 is at most n – 1.

Local maximum point – highest point or “peak” in an interval
 function values at these points are called local maxima

Local minimum point – lowest point or “valley” in an interval
 function values at these points are called local minima

Extrema – plural of extremum, includes all local maxima and local
minima

19. Extrema

20. Number of Local Extrema





A linear function has degree 1 and no local
extrema.
A quadratic function has degree 2 with one
extreme point.
A cubic function has degree 3 with at most
two local extrema.
A quartic function has degree 4 with at most
three local extrema.
How does this relate to the number of
turning points?

21. Comprehensive Graphs

The most important features of the graph of a
polynomial function are:
intercepts,
2.
extrema,
3.
end behavior.
A comprehensive graph of a polynomial function
will exhibit the following features:
1.
all x-intercepts (if any),
2.
the y-intercept,
3.
all extreme points (if any),
4.
enough of the graph to exhibit end
behavior.
1.
