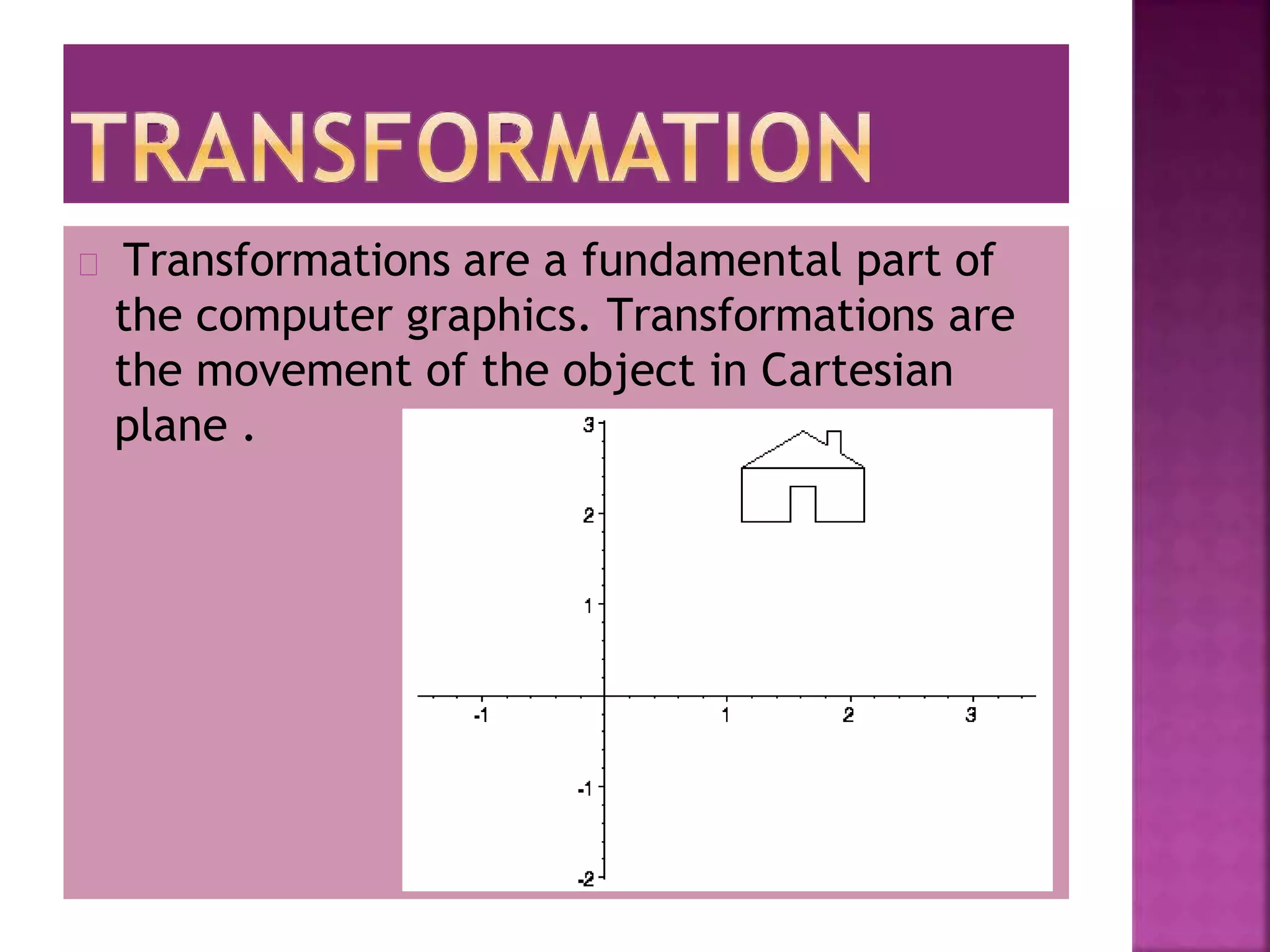
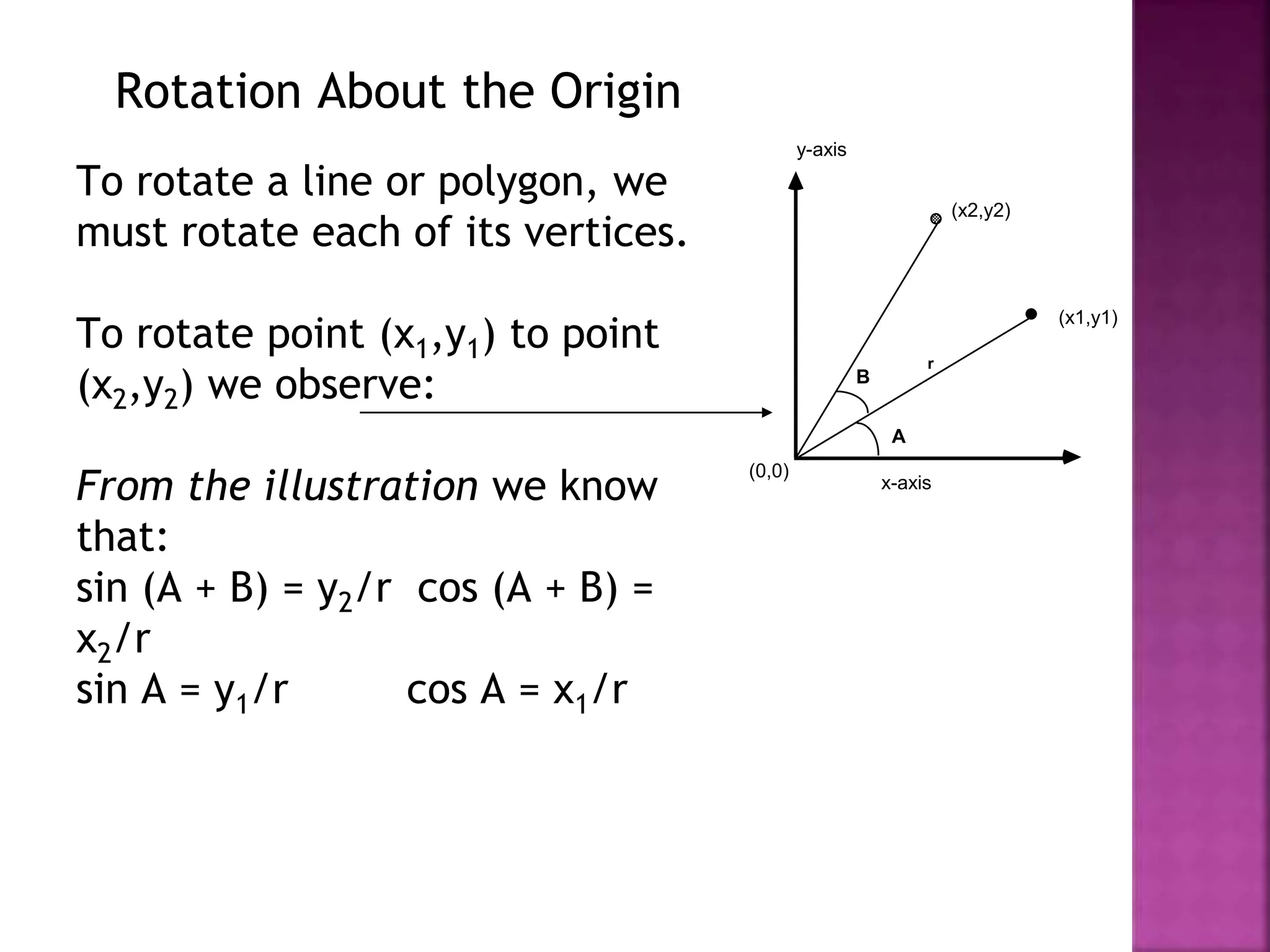
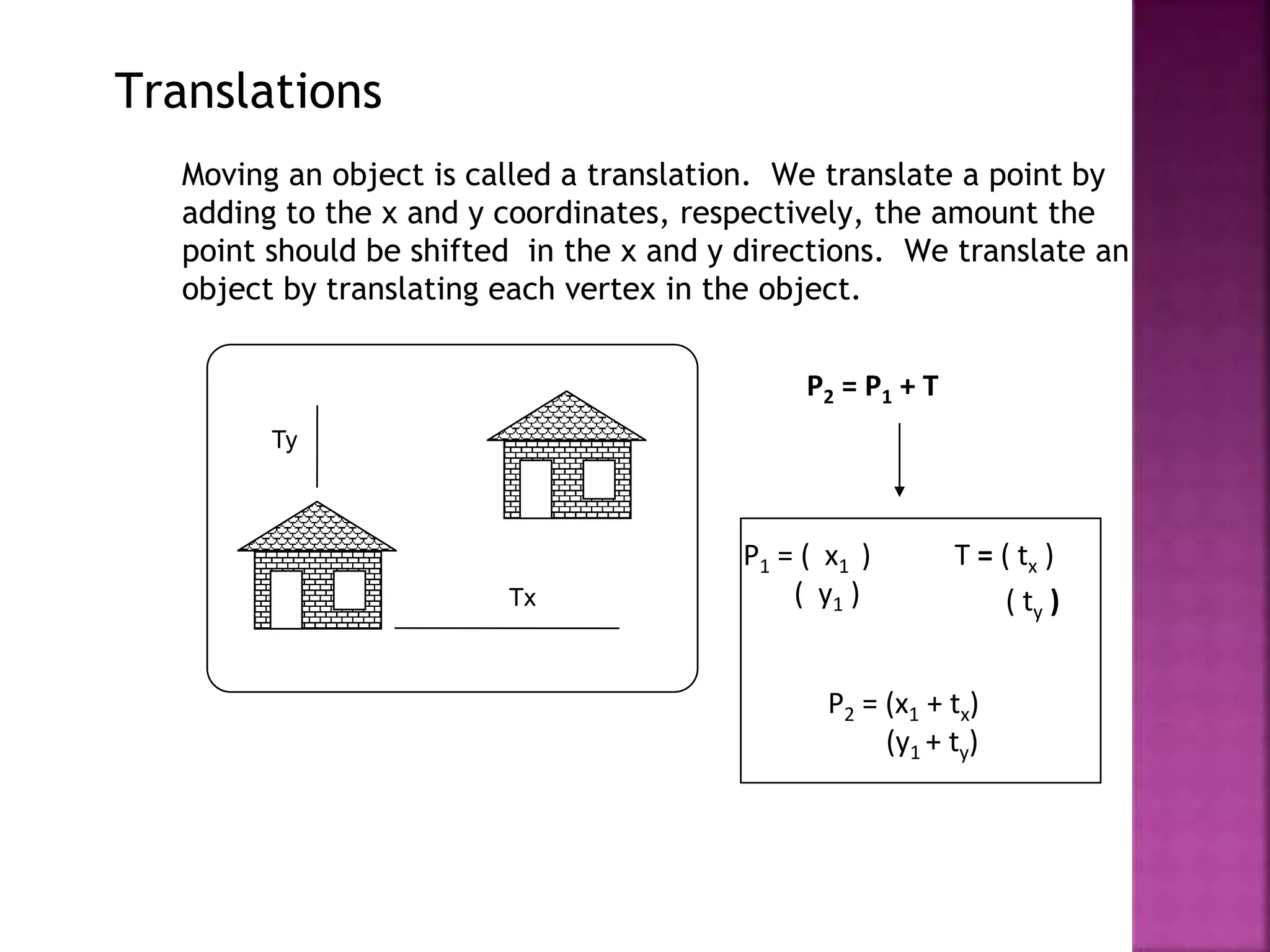
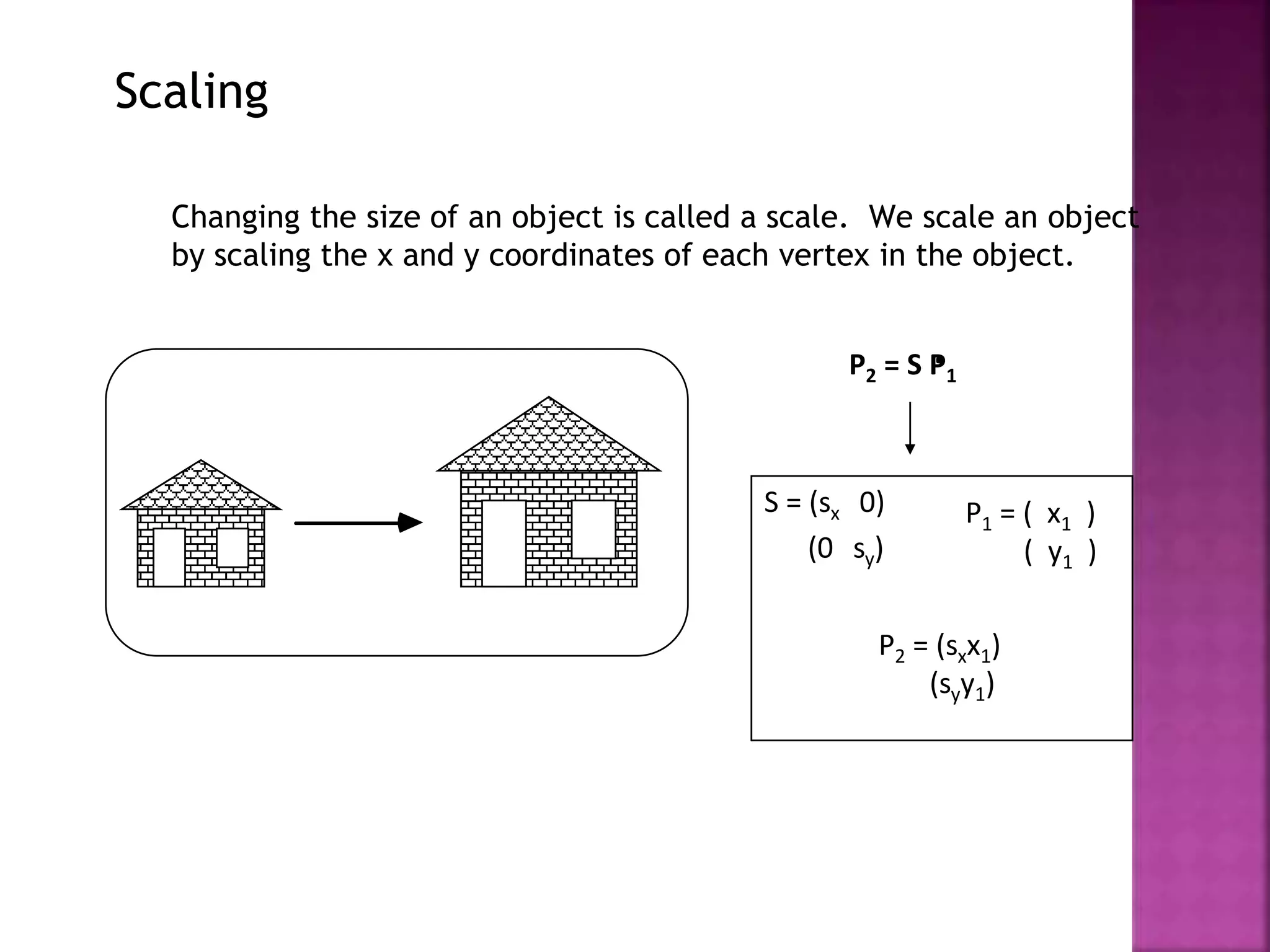
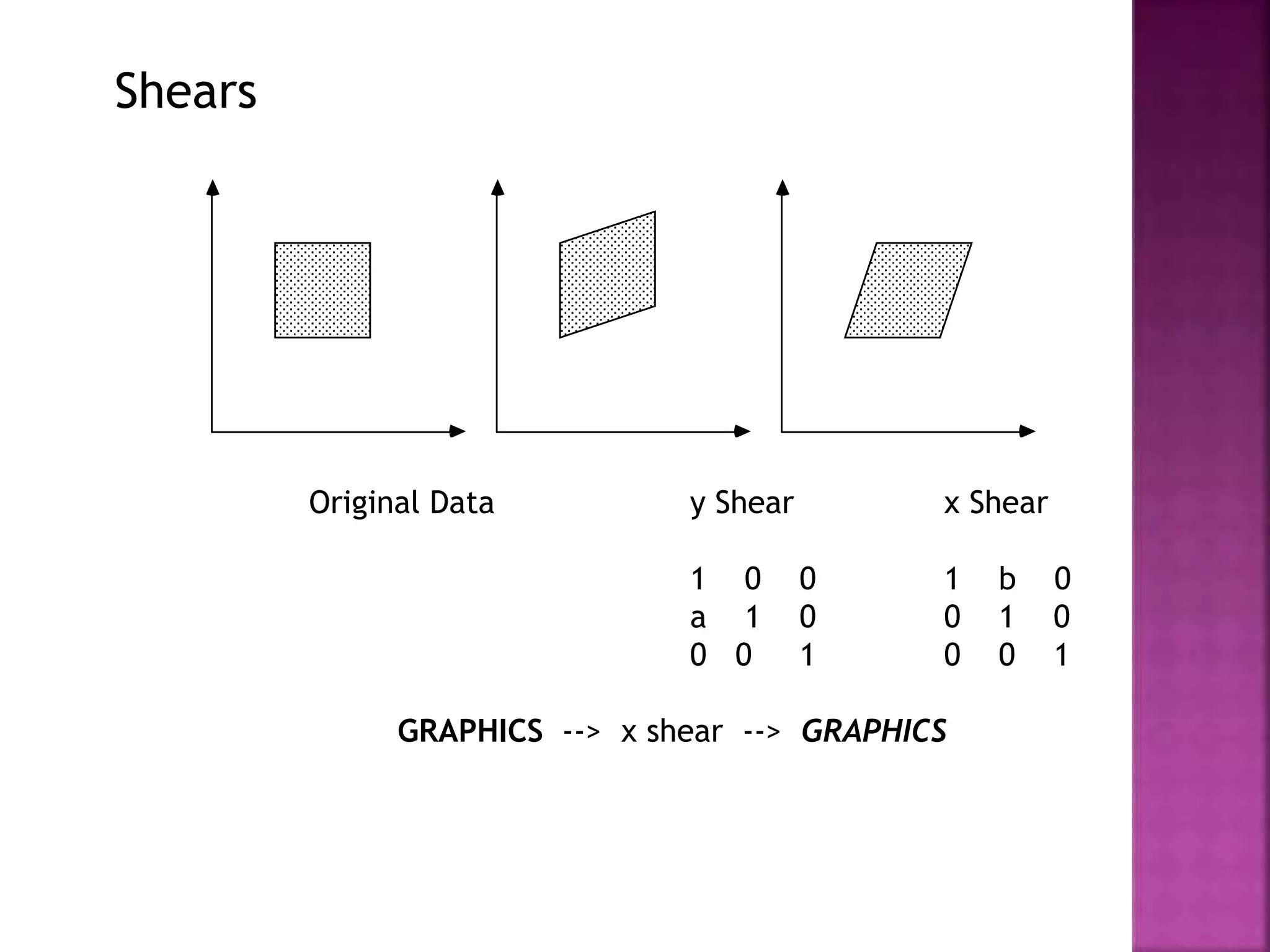
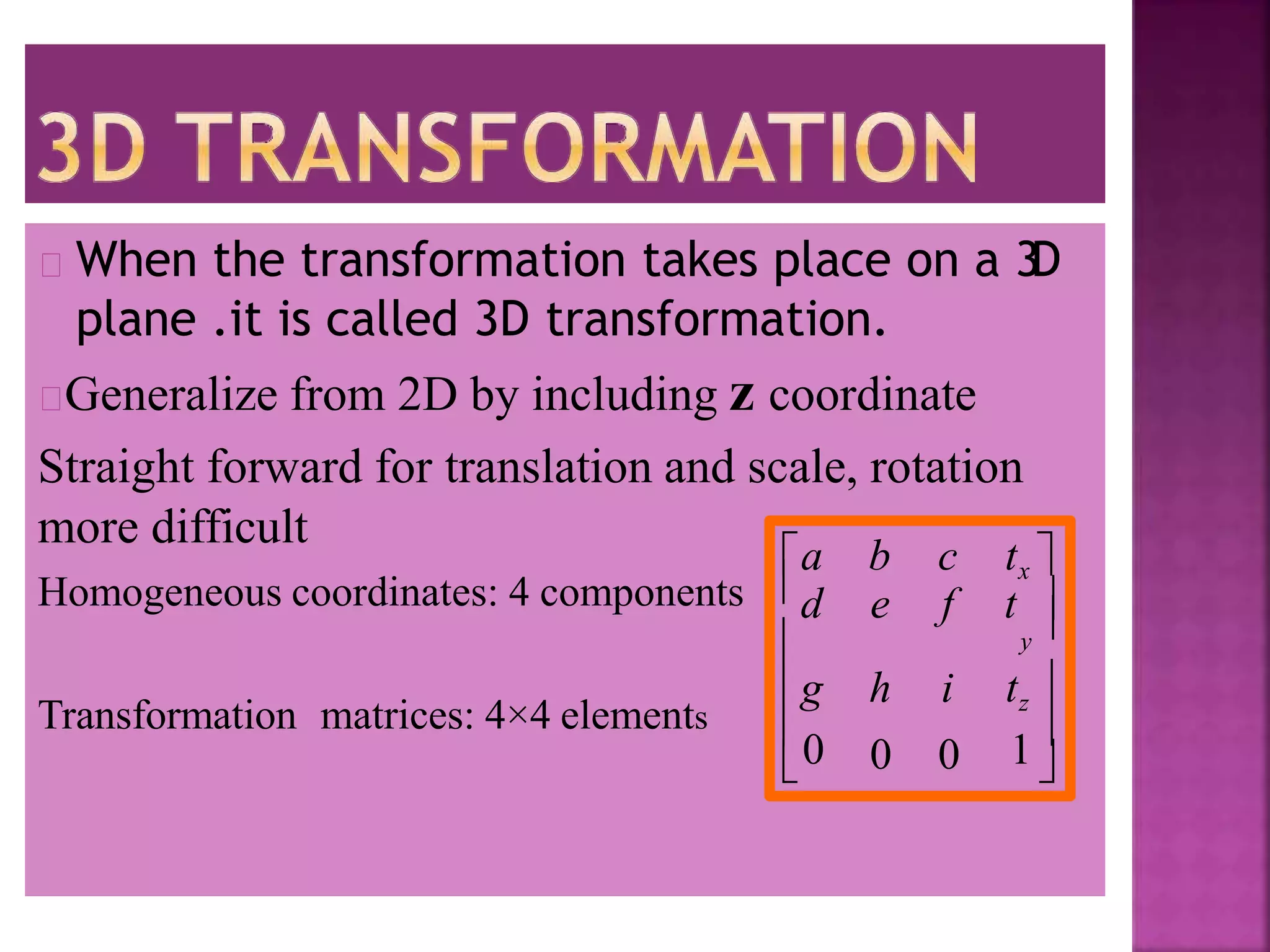
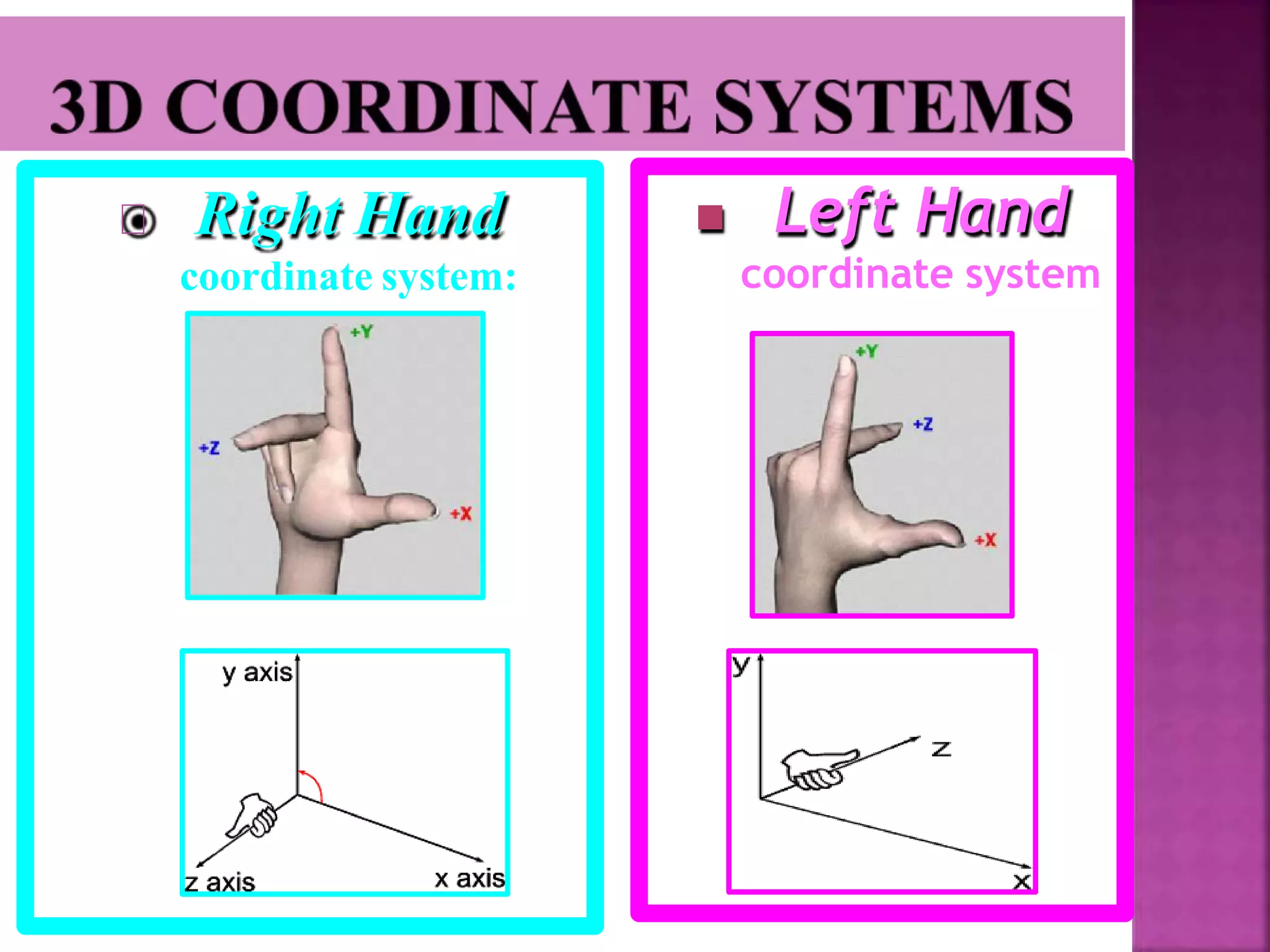
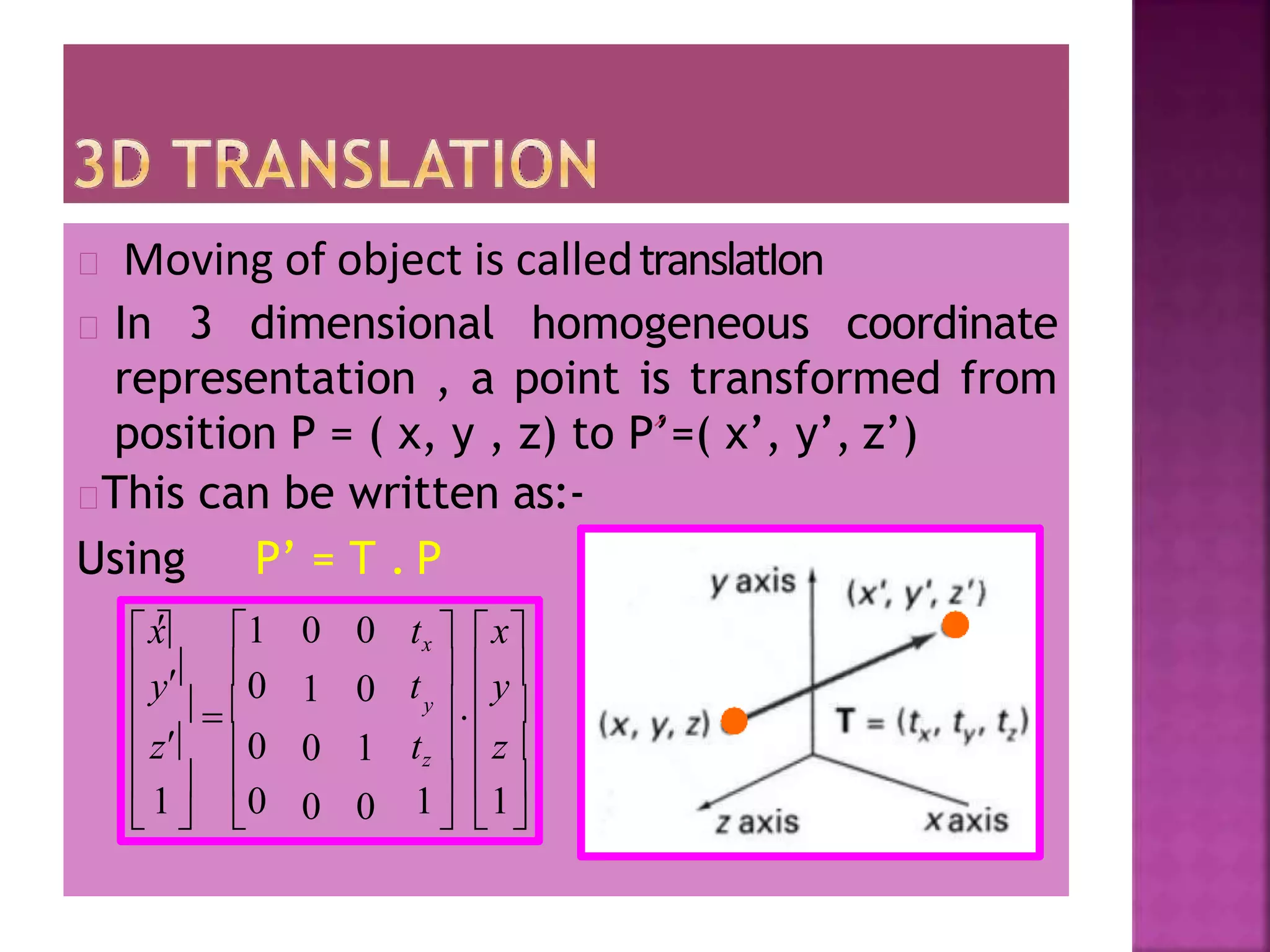
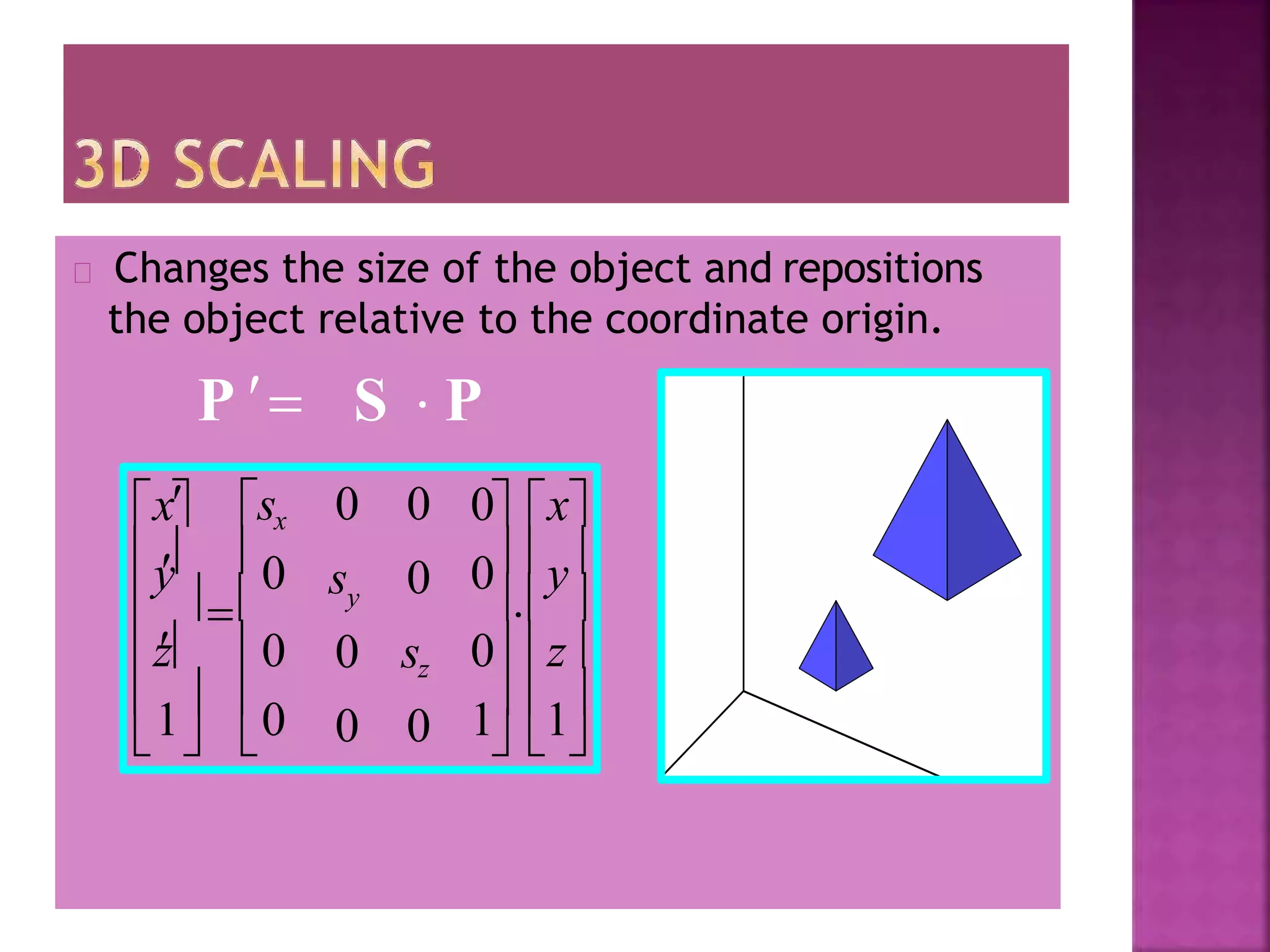
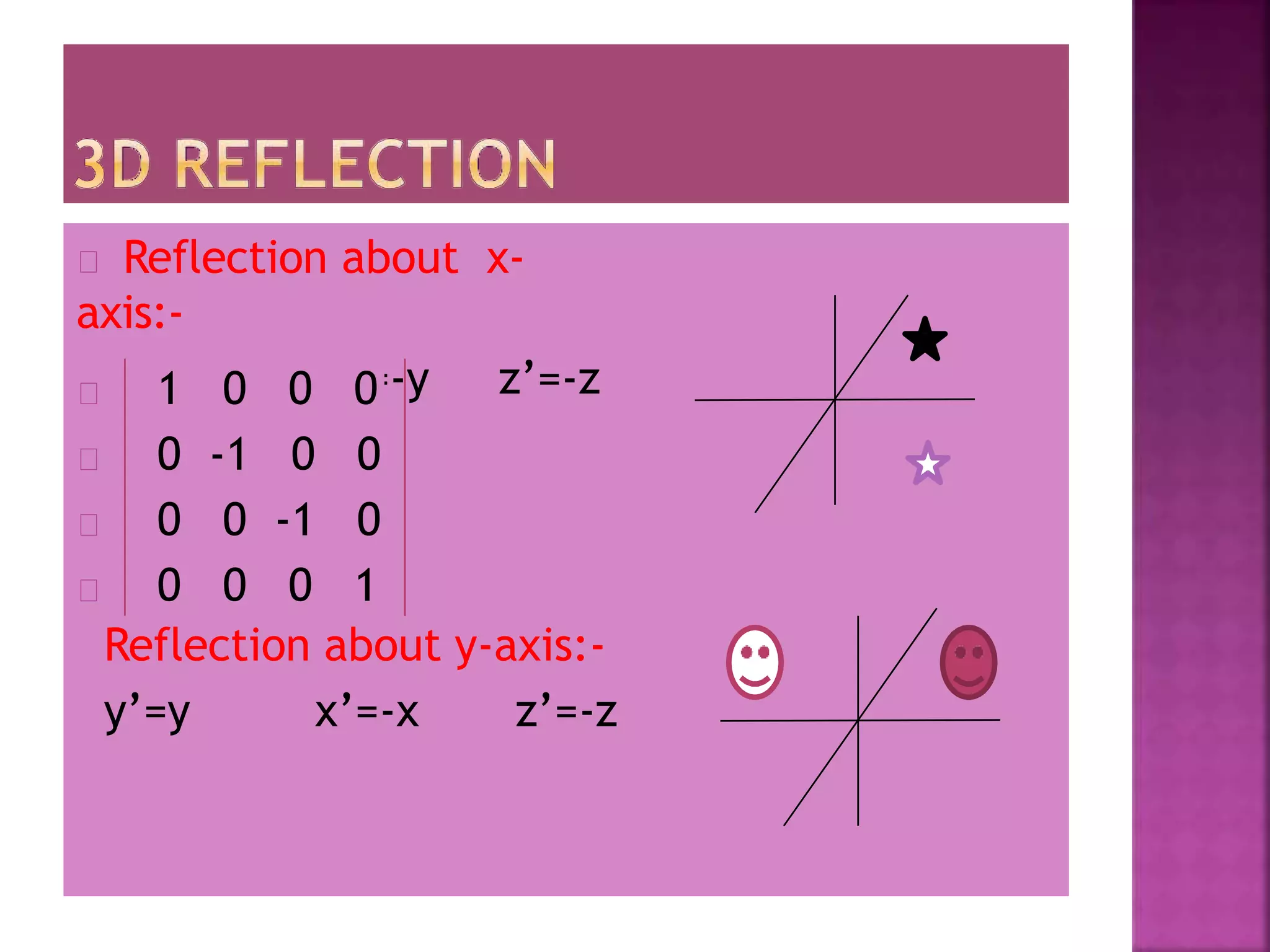
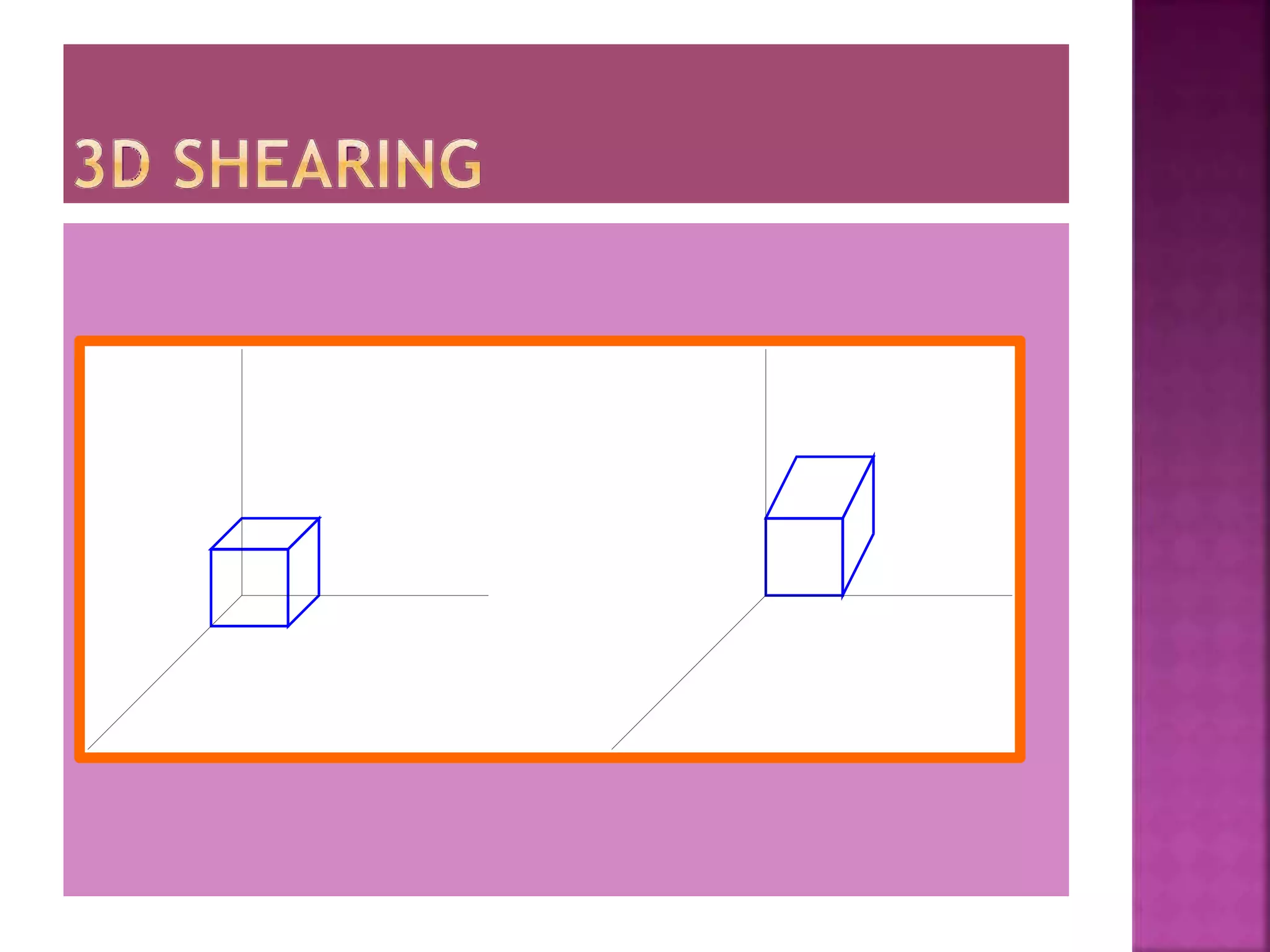
This document discusses different types of 2D and 3D geometric transformations in computer graphics, including translation, rotation, scaling, shearing, and reflection. It provides examples of how to mathematically represent these transformations using matrix multiplication and homogeneous coordinates. Transformations are used to position and modify 3D objects, change viewing positions, and affect how something is viewed.

1. GEOMETRIC TRANFORMATION
2D & 3D

2. Daffodil International University
Submitted To:
Umme Hafsa Billah
Sr. Lecturer
Daffodil International University
Submitted By:
Nirnay Mukharjee – 143-15-4421

3. Transformations are a fundamental part of
the computer graphics. Transformations are
the movement of the object in Cartesian
plane .

4. There are two types of transformation in
computer graphics.
1) 2D transformation
2) 3D transformation
Types of 2D and 3D transformation
1) Translation
2) Rotation
3) Scaling
4) Shearing
5) Mirror reflection

5. Transformation are used to position
objects , to shape object , to change
even howviewing positions , and
something is viewed.
In simple words transformation is used for
1) Modeling
2) viewing

6. When the transformation takes place on a 2D
plane .it is called 2D transformation.
2D means two dimensional (x-axis and Y-axis)
Object Transformation in 2D
 Alter the coordinates descriptions an object
 Translation , rotation , scaling , shearing,
 reflection.
 Coordinate system unchanged
Coordinate transformation in 2D
 Produce a different coordinate system

7. Rotation About the Origin
To rotate a line or polygon, we
must rotate each of its vertices.
To rotate point (x1,y1) to point
(x2,y2) we observe:
From the illustration we know
that:
sin (A + B) = y2/r cos (A + B) =
x2/r
sin A = y1/r cos A = x1/r
x-axis
(x1,y1)
(x2,y2)
A
B
r
(0,0)
y-axis

8. Translations
Moving an object is called a translation. We translate a point by
adding to the x and y coordinates, respectively, the amount the
point should be shifted in the x and y directions. We translate an
object by translating each vertex in the object.
P2 = P1 + T
T = ( tx )
( ty )
P1 = ( x1 )
( y1 )
P2 = (x1 + tx)
(y1 + ty)
Ty
Tx

9. Scaling
Changing the size of an object is called a scale. We scale an object
by scaling the x and y coordinates of each vertex in the object.
P2 = S P1
.
S = (sx 0)
(0 sy)
P1 = ( x1 )
( y1 )
P2 = (sxx1)
(syy1)

10. Shears
Original Data y Shear x Shear
1 0 0 1 b 0
a 1 0 0 1 0
0 0 1 0 0 1
GRAPHICS --> x shear --> GRAPHICS

11. When the transformation takes place on a 3D
plane .it is called 3D transformation.
Generalize from 2D by including z coordinate
Straight forward for translation and scale, rotation
more difficult
Homogeneous coordinates: 4 components
Transformation matrices: 4×4 elements

 10
tz 
a b c tx 
d e f t  y
g h i
0 0

12. Right Hand
coordinate system:
 Left Hand
coordinate system

13. Moving of object is calledtranslatIon
In 3 dimensional homogeneous coordinate
representation , a point is transformed from
position P = ( x, y , z) to P’=( x’, y’, z’)
This can be written as:-
Using P’ = T . P
  
   
   1 1
1 0 0
1 0
0 1
0 0
1  0
t  y
z 0
y 0
x
tz  z
y  
tx  x

14. where an object is to be rotated about an axis that is
parallel to one of the coordinate axis, we can
obtain the desired rotation with the following
transformation sequence.
Coordinate axis rotation
Z- axis Rotation(Roll)
Y-axis Rotation(Yaw)
X-axis Rotation(Pitch)

15. Changes the size of the object and repositions
the object relative to the coordinate origin.
P  S  P
 
  
 
   1 11 0
0 z
0 y
0 x
z 0
y 0
x
y
sx 0 0
s 0
0 sz
0 0

16. , and
Reflection in computer graphics is used to
emulate reflective objects like mirrors and
shiny surfaces
Reflection may be an x-axis
y-axis , z-axis. and also in
the planes xy-plane,yz-plane
zx-plane.
Reflection relative to a given
Axis are equivalent to 180
Degree rotations

17. Reflection about x-
axis:-
x’=x y’=-y z’=-z
Reflection about y-axis:-
y’=y x’=-x z’=-z
1 0 0 0
0 -1 0 0
0 0 -1 0
0 0 0 1

18.  Modify object shapes
 Useful for perspective projections
 When an object is viewed from different
directions and at different distances, the
appearance of the object will be different.
Such view is called perspective view.
Perspective projections mimic what the
human eyes see.
E.g. draw a cube (3D) on a screen (2D) Alter the
values for x and y by an amount proportional to
the distance from zref

20. Thank you!!