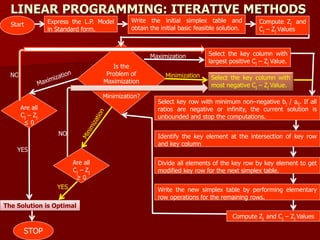
This document discusses linear programming iterative methods. It introduces the simplex method, two-phase simplex method, and Big M method. An example problem is provided to illustrate solving a linear programming problem using these iterative methods. The problem involves maximizing profit from producing tables and chairs given resource constraints. The problem is formulated and solved using the simplex method in multiple steps.

1. ADVANCED
OPERATIONS
RESEARCH
By: -
Hakeem–Ur–Rehman
IQTM–PU
A RO
LP: ITERATIVE METHODS

2. LINEAR PROGRAMMING: ITERATIVE METHODS
1. Simplex Method
2. The "Big M method" or the Charnes method of penalty
3. Two Phase Simplex Method
BASIC CONCEPTS:
 Basic Solution (BS): Each solution to any system of equations is called a Basic Solution (BS).
 Basic Feasible Solution (BFS): A Basic Feasible Solution (BFS) satisfies the model constraints and has
the same number of variables with nonnegative values as there are constraints.
 Non-Basic Variables (NBV): The variables that equal to zero at a basic feasible solution point are
called Non-Basic Variables (NBV).
 Basic Variables (BV): The variables which have values (other than zero) at a basic feasible solution point
are called Basic Variables (BV).
 Slack & Surplus: Slack is the leftover of a resource. Surplus is the excess of production.
 Entering Basic Variables (Incoming variable): The variables that go from non-basic variables (which
increase from Zero) to basic variables are called the Entering Basic Variables.
 Leaving Basic Variables (Outing Variable): The variables that go from basic variables (which drop to
Zero) to non-basic variables are called the Leaving Basic Variables.
 Minimum Replacement Ratio Test: The Minimum replacement Ratio Test is to determine which basic
variable drops to zero first as the entering basic variable increased.

3. LINEAR PROGRAMMING: ITERATIVE METHODS
EXAMPLE: ABC Furniture Company produces computer tables and chairs on a daily basis. Each
computer table produced results in Rs. 160 in profit; each chair results in Rs. 200 in profit. The
production of computer tables and chairs is dependent on the availability of limited resources:
Labor, Wood, and Storage Space. The resource requirements for the production of tables and
chairs and the total resources available are as follows.
RESOURCE REQUIREMENTS
Resources Computer Table Chair Total Available per day
Labor (hour) 2 4 40
Wood (feet) 18 18 216
Storage (Square feet) 24 12 240
The company wants to know the number of computer tables and chairs to produce per day in order
to maximize the profit.
SOLUTION: Let ‘X1’ and ‘X2’ be the number of computer tables and chairs are
produced respectively.
The complete formulation of the LP problem is as follow:
Maximize: Z = 160X1 + 200X2
Subject to:
2X1 + 4X2 ≤ 40 (Labor Constraint)
18X1 + 18X2 ≤ 216 (Wood Constraint)
24X1 + 12X2 ≤ 240 (Storage Constraint)
X1, X2 ≥ 0

4. LINEAR PROGRAMMING: ITERATIVE METHODS
Start Express the L.P. Model
in Standard form.
Write the initial simplex table and
obtain the initial basic feasible solution.
Compute Zj and
Cj – Zj Values
Is the
Problem of
Maximization
or
Minimization?
Maximization Select the key column with
largest positive Cj – Zj Value.
Select key row with minimum non–negative bj / aij. If all
ratios are negative or infinity, the current solution is
unbounded and stop the computations.
Select the key column with
most negative Cj – Zj Value.
Minimization
Identify the key element at the intersection of key row
and key column
Divide all elements of the key row by key element to get
modified key row for the next simplex table.
Write the new simplex table by performing elementary
row operations for the remaining rows.
Compute Zj and Cj – Zj Values
Are all
Cj – Zj
≤ 0
The Solution is Optimal
YES
Are all
Cj – Zj
≥ 0
YES
NO
NO
STOP

5. LINEAR PROGRAMMING: ITERATIVE METHODS
Standard LP Form:
Maximize: Z = 160X1 + 200X2 + 0S1 + 0S2 + 0S3
Subject to:
2X1 + 4X2 + S1 = 40
18X1 + 18X2 + S2 = 216
24X1 + 12X2 + S3 = 240
X1, X2, S1, S2, S3 ≥ 0
SOLUTION: Let ‘X1’ and ‘X2’ be the number of computer tables and chairs are
produced respectively.
The complete formulation of the LP problem is as follow:
Maximize: Z = 160X1 + 200X2
Subject to:
2X1 + 4X2 ≤ 40 (Labor Constraint)
18X1 + 18X2 ≤ 216 (Wood Constraint)
24X1 + 12X2 ≤ 240 (Storage Constraint)
X1, X2 ≥ 0

6. LINEAR PROGRAMMING: ITERATIVE METHODS
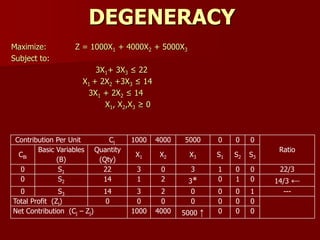
Standard LP Form:
Maximize: Z = 160X1 + 200X2 + 0S1 + 0S2 + 0S3
Subject to:
2X1 + 4X2 + S1 = 40
18X1 + 18X2 + S2 = 216
24X1 + 12X2 + S3 = 240
X1, X2, S1, S2, S3 ≥ 0
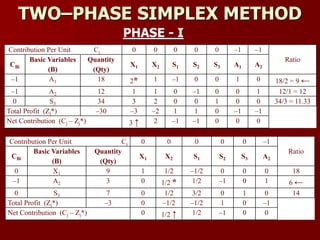
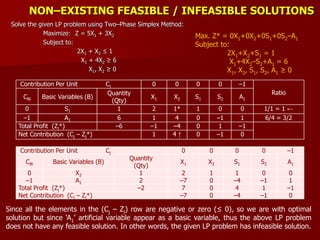
Contribution Per Unit Cj 160 200 0 0
0
Ratio = [Qty / PE > 0]
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 S3
0 S1 40 2 4* 1 0 0 40/4 = 10 ←
0 S2 216 18 18 0 1 0 216/18 = 12
0 S3 240 24 12 0 0 1 240/12 = 20
Total Profit (Zj) 0 0 0 0 0 0
Net Contribution (Cj – Zj) 160 200 ↑ 0 0
0

7. LINEAR PROGRAMMING: ITERATIVE METHODS
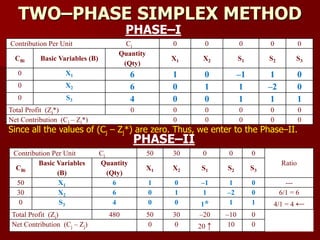
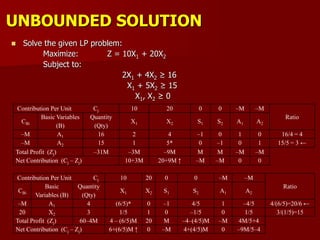
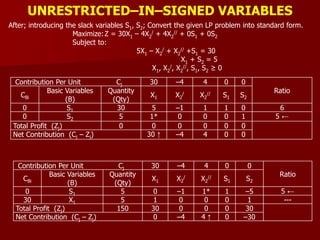
Contribution Per Unit Cj 160 200 0 0 0
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 S3
200 X2 8 0 1 1/2 –1/18 0
160 X1 4 1 0 –1/2 1/9 0
0 S3 48 0 0 6 –2 1
Total Profit (Zj) 2240 160 200 20 20/3 0
Net Contribution (Cj – Zj) 0 0 –20 –20/3 0
Since all the values of (Cj – Zj) ≤ 0; so, the solution is optimal. Optimal solution is
2240 for Max. ‘Z’; at X1= 4, X2= 8.
Contribution Per Unit Cj 160 200 0 0 0
Ratio = [Qty / PE > 0]
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 S3
200 X2 10 1/2 1 1/4 0 0 10/(1/2) = 20
0 S2 36 9* 0 –9/2 1 0 36/9 = 4 ←
0 S3 120 18 0 –3 0 1 120/18 = 20/3
Total Profit (Zj) 2000 100 200 50 0 0
Net Contribution (Cj – Zj) 60 ↑ 0 –50 0 0

8. BIG ‘M’ METHOD: QUESTION
Use Big ‘M’ method to solve the LP problem.
Minimize: Z = 8X1 + 4X2
Subject to:
3X1 + X2 ≥ 27
X1 + X2 = 21
X1 + 2X2 ≤ 40
X1 , X2 ≥ 0
LINEAR PROGRAMMING: ITERATIVE METHODS

9. LINEAR PROGRAMMING: ITERATIVE METHODS
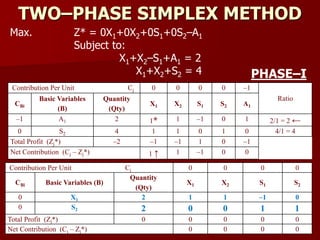
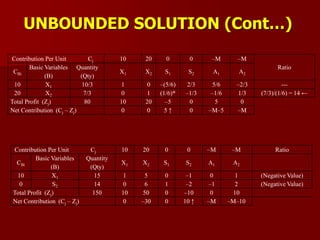
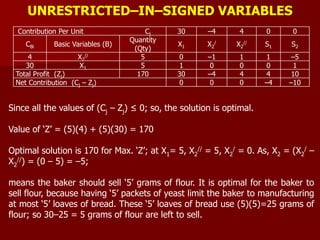
Maximize: Z = –8X1 –4X2 + 0S1 + 0S2 – MA1 – MA2
Subject to:
3X1+ X2–S1+A1 = 27
X1+ X2+A2 = 21
X1+2X2+S2 = 40
X1, X2, S1, S2, A1, A2 ≥ 0
Contribution Per Unit Cj –8 –4 0 0 –M –M
Ratio=
[Qty/PE>0]CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 A1 A2
–M A1 27 3* 1 –1 0 1 0 27/3 = 9 ←
–M A2 21 1 1 0 0 0 1 21/1 = 21
0 S2 40 1 2 0 1 0 0 40/1 = 40
Total Profit (Zj) –48M –4M –2M M 0 –M –M
Net Contribution (Cj – Zj) –8+4M ↑ –4+2M –M 0 0 0
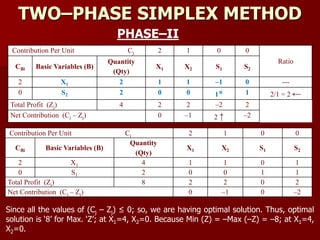
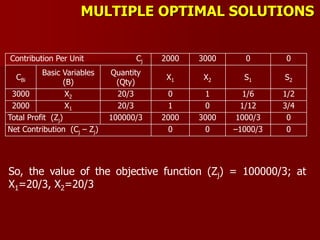
Contribution Per Unit
Cj
–8 –4 0 0 –M –M
Ratio
CBi
Basic
Variables (B)
Quantity
(Qty)
X1 X2 S1 S2 A1 A2
–8 X1 9 1 1/3 –1/3 0 1/3 0 27
–M A2 12 0 (2/3)* 1/3 0 –1/3 1 18 ←
0 S2 31 0 5/3 1/3 1 –1/3 0 18.6
Total Profit (Zj) –72–12M –8 –8/3–(2/3)M 8/3–M/3 0 –8/3+M/3 –M
Net Contribution (Cj – Zj) 0 –4/3+(2/3)M
↑
–8/3+M/3 0 8/3– (2/3)M 0

10. LINEAR PROGRAMMING: ITERATIVE METHODS
Contribution Per Unit Cj –8 –4 0 0 –M –M
CBi Basic Variables (B)
Quantity
(Qty)
X1 X2 S1 S2 A1 A2
–8 X1 3 1 0 –1/2 0 1/2 –1/2
–4 X2 18 0 1 1/2 0 –1/2 3/2
0 S2 1 0 0 –1/2 1 1/2 –5/2
Total Profit (Zj) –96 –8 –4 2 0 –2 –2
Net Contribution (Cj – Zj) 0 0 –2 0 –M+2 –M+2
Optimal solution is –96 for Max. ‘Z’; at X1= 3, X2= 18.
Because Min (Z) = –Max (–Z) = 96; at X1= 3, X2= 18.
Use Big ‘M’ method to solve the LP problem.
Minimize: Z = –2X1 – X2
Subject to:
X1+ X2 ≥ 2
X1 + X2 ≤ 4
X1, X2 ≥ 0

11. TWO PHASE SIMPLEX METHOD
 The Two–Phase Simplex method consists of the following steps:
PHASE–1
 STEP–1:
– The objective function of the given LP problem must be in the form of Maximized. If it is to
be minimized then we convert it into a problem of Maximization by Max Z = – Min (–Z).
– Check whether all the values on the right hand side of the constraints must be positive. If
any one of them is negative then multiply that constraint with (–1).
 STEP–2:
– Express the problem in standard form by introducing slack, surplus and artificial variables.
And Assign a cost ‘–1’ to each artificial variable while a cost ‘0’ to all other variables and
formulate a new objective function ‘Z*’.
– Write down the auxiliary LP problem in which new objective function is to be maximized
subject to the given constraints.
 STEP–3: Solve the auxiliary LP problem by simplex method until and obtain the optimum
basic feasible solution. If (Cj – Zj*) row indicates optimal solution as it contains all zero or
negative elements and if:
– the artificial variable appears as a basic variable then the given LP problem has infeasible
solution so we terminate our solution in Phase–1.
– the artificial variable does not appear as a basic variable then the given LP problem has a
feasible solution and we proceed to Phase–II.

12. TWO PHASE SIMPLEX METHOD
PAHSE–II
Use the optimum basic feasible solution of Phase–I as a
starting solution for the original LP problem.
Assign the actual costs to the variables in the objective
function and a zero cost to every artificial variable in the
basis at zero level.
Delete the artificial variable columns from the table which
is eliminated from the basis in Phase–I.
Apply simplex algorithm to the modified simplex table
obtained at the end of Phase–I till an optimum basic
feasible is obtained or till there is an indication of
unbounded solution.

13. TWO–PHASE SIMPLEX METHOD
EXAMPLE:
Use Two–Phase Simplex method to solve the LP problem.
Maximize: Z = 50X1 + 30X2
Subject to:
2X1+ X2 ≥ 18
X1 + X2 ≥ 12
3X1+2X2 ≤ 34
X1, X2 ≥ 0
STANDARD FORM:
Max. Z* = 0X1+0X2+0S1+0S2+0S3–A1–A2
Subject to:
2X1+X2–S1+A1 = 18
X1+X2–S2+A2 = 12
3X1+2X2+S3 = 34

14. TWO–PHASE SIMPLEX METHOD
Contribution Per Unit Cj 0 0 0 0 0 –1 –1
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 S3 A1 A2
–1 A1 18 2* 1 –1 0 0 1 0 18/2 = 9 ←
–1 A2 12 1 1 0 –1 0 0 1 12/1 = 12
0 S3 34 3 2 0 0 1 0 0 34/3 = 11.33
Total Profit (Zj*) –30 –3 –2 1 1 0 –1 –1
Net Contribution (Cj – Zj*) 3 ↑ 2 –1 –1 0 0 0
PHASE - I
Contribution Per Unit Cj 0 0 0 0 0 –1
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 S3 A2
0 X1 9 1 1/2 –1/2 0 0 0 18
–1 A2 3 0 1/2 * 1/2 –1 0 1 6 ←
0 S3 7 0 1/2 3/2 0 1 0 14
Total Profit (Zj*) –3 0 –1/2 –1/2 1 0 –1
Net Contribution (Cj – Zj*) 0 1/2 ↑ 1/2 –1 0 0

15. TWO–PHASE SIMPLEX METHOD
PHASE–I
Contribution Per Unit Cj 0 0 0 0 0
CBi Basic Variables (B)
Quantity
(Qty)
X1 X2 S1 S2 S3
0 X1 6 1 0 –1 1 0
0 X2 6 0 1 1 –2 0
0 S3 4 0 0 1 1 1
Total Profit (Zj*) 0 0 0 0 0 0
Net Contribution (Cj – Zj*) 0 0 0 0 0
PHASE–II
Since all the values of (Cj – Zj*) are zero. Thus, we enter to the Phase–II.
Contribution Per Unit Cj 50 30 0 0 0
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 S3
50 X1 6 1 0 –1 1 0 ---
30 X2 6 0 1 1 –2 0 6/1 = 6
0 S3 4 0 0 1* 1 1 4/1 = 4 ←
Total Profit (Zj) 480 50 30 –20 –10 0
Net Contribution (Cj – Zj) 0 0 20 ↑ 10 0

16. TWO–PHASE SIMPLEX METHOD
PHASE–II
Contribution Per Unit Cj 50 30 0 0 0
CBi Basic Variables (B)
Quantity
(Qty)
X1 X2 S1 S2 S3
50 X1 10 1 0 0 2 1
30 X2 2 0 1 0 –3 –1
0 S1 4 0 0 1 1 1
Total Profit (Zj) 560 50 30 0 10 20
Net Contribution (Cj – Zj) 0 0 0 –10 –20
Since all the values of (Cj – Zj) ≤ 0; So, we are having optimal
solution.
Thus, Zj = 560 at X1=10 and X2=2.
Use Two–Phase Simplex method to solve the LP problem.
Minimize: Z = –2X1 – X2
Subject to:
X1+ X2 ≥ 2
X1 + X2 ≤ 4
X1, X2 ≥ 0

17. TWO–PHASE SIMPLEX METHOD
Max. Z* = 0X1+0X2+0S1+0S2–A1
Subject to:
X1+X2–S1+A1 = 2
X1+X2+S2 = 4
Contribution Per Unit Cj 0 0 0 0 –1
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 A1
–1 A1 2 1* 1 –1 0 1 2/1 = 2 ←
0 S2 4 1 1 0 1 0 4/1 = 4
Total Profit (Zj*) –2 –1 –1 1 0 –1
Net Contribution (Cj – Zj*) 1 ↑ 1 –1 0 0
Contribution Per Unit Cj 0 0 0 0
CBi Basic Variables (B)
Quantity
(Qty)
X1 X2 S1 S2
0 X1 2 1 1 –1 0
0 S2 2 0 0 1 1
Total Profit (Zj*) 0 0 0 0 0
Net Contribution (Cj – Zj*) 0 0 0 0
PHASE–I

18. TWO–PHASE SIMPLEX METHOD
PHASE–II
Contribution Per Unit Cj 2 1 0 0
Ratio
CBi Basic Variables (B)
Quantity
(Qty)
X1 X2 S1 S2
2 X1 2 1 1 –1 0 ---
0 S2 2 0 0 1* 1 2/1 = 2 ←
Total Profit (Zj) 4 2 2 –2 2
Net Contribution (Cj – Zj) 0 –1 2 ↑ –2
Contribution Per Unit Cj 2 1 0 0
CBi Basic Variables (B)
Quantity
(Qty)
X1 X2 S1 S2
2 X1 4 1 1 0 1
0 S1 2 0 0 1 1
Total Profit (Zj) 8 2 2 0 2
Net Contribution (Cj – Zj) 0 –1 0 –2
Since all the values of (Cj – Zj) ≤ 0; so, we are having optimal solution. Thus, optimal
solution is ‘8’ for Max. ‘Z’; at X1=4, X2=0. Because Min (Z) = –Max (–Z) = –8; at X1=4,
X2=0.

19. LINEAR PROGRAMMING: SPECIAL
CASES USING ITERATIVE METHODS
The following variants are being considered:
1. Tie for the key (Pivot) column
2. Degeneracy (Tie for the Key (Pivot) row)
3. Unbounded solution
4. Multiple solutions
5. Non-existing feasible solution / Infeasible
solution
6. Unrestricted–in–sign variables

20. DEGENERACY:
(Tie for the Key (Pivot) row)
 Graphically, degeneracy occurs when three or more
constraints intersect in the solution of a problem
with two variables
 Degeneracy will arise at the initial stage of the
simplex method if at least one basic variable should
be zero in the initial basic feasible solution
 Degeneracy will arise at any iteration of the simplex
method where more than one variable is eligible to
leave the basis (i.e. Tie for the key (pivot) row)

21. METHOD TO RESOLVE DEGENERACY
 Step–1: First find out the rows for which the minimum non–
negative ratio is the same (Tie).
 Step–2: Now rearrange the columns of the simplex table so that
the columns forming the identity (Unit) matrix come first.
 Step–3: Now find the minimum ratios of the simplex table
columns from left to right one by one which shows the identity
matrix, only for the tied rows until tie had not been broken.
Whenever tie has been broken, choose that particular row which
has minimum positive ratio as a Key row. Use the formula for the
minimum ratios is:
=(Elements of the particular identity matrix column)/(Corresponding
elements of the Key column)
 After resolve the degeneracy, Simplex method is applied to obtain
the optimum solution.

22. DEGENERACY
Maximize: Z = 1000X1 + 4000X2 + 5000X3
Subject to:
3X1+ 3X3 ≤ 22
X1 + 2X2 +3X3 ≤ 14
3X1 + 2X2 ≤ 14
X1, X2,X3 ≥ 0
Contribution Per Unit Cj 1000 4000 5000 0 0 0
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 X3 S1 S2 S3
0 S1 22 3 0 3 1 0 0 22/3
0 S2 14 1 2 3* 0 1 0 14/3 ←
0 S3 14 3 2 0 0 0 1 ---
Total Profit (Zj) 0 0 0 0 0 0 0
Net Contribution (Cj – Zj) 1000 4000 5000 ↑ 0 0 0

23. DEGENERACY (Cont…)
Contribution Per Unit Cj 1000 4000 5000 0 0 0
Ratio
CBi
Basic
Variables
Quantity
(Qty)
X1 X2 X3 S1 S2 S3
0 S1 8 2 –2 0 1 –1 0 ---
5000 X3 14/3 1/3 (2/3) 1 0 1/3 0 (14/3) / (2/3) = 7
TIE
0 S3 14 3 2 0 0 0 1 14 / 2 = 7
Total Profit (Zj) 70,000/3 5000/3 10,000/3 5000 0 5000/3 0
Net Contribution (Cj – Zj) –2000/3 2000/3 ↑ 0 0 –5000/3 0
Contribution Per Unit Cj 0 5000 0 1000 4000 0 Ratio
CBi
Basic
Variables
Quantity
(Qty)
S1 X3 S3 X1 X2 S2 (S1/X2) (X3/X2)
0 S1 8 1 0 0 2 –2 –1 --- ---
5000 X3 14/3 0 1 0 1/3 2/3 1/3 0/(2/3)=0 1/(2/3) =3/2
0 S3 14 0 0 1 3 2* 0 0/2 = 0 0/2 = 0 ←
Total Profit (Zj) 70,000/3 0 5000 0 5000/3 10,000/3 5000/3
Net Contribution (Cj – Zj) 0 0 0 –2000/3 2000/3 ↑ –5000/3

24. DEGENERACY (Cont…)
Contribution Per Unit Cj 0 5000 0 1000 4000 0
CBi
Basic
Variables (B)
Quantity
(Qty)
S1 X3 S3 X1 X2 S2
0 S1 22 1 0 1 5 0 –1
5000 X3 0 0 1 –1/3 –2/3 0 1/3
4000 X2 7 0 0 1/2 3/2 1 0
Total Profit (Zj) 28000 0 5000 1000/3 8000/3 4000 5000/3
Net Contribution (Cj – Zj) 0 0 –1000/3 –5000/3 0 –5000/3
Optimal solution is 28000 for Max. ‘Z’; at X1=0, X2=7, X3=0.

25. UNBOUNDED SOLUTION
 When no variable qualifies to be the outgoing
(leaving) variable then a linear programming
problem would be unbounded such situation
arise if the incoming (entering) variable could
be increased indefinitely without giving negative
values to any of the current basic variables. In
tabular form, this means that every coefficient
in the key column (excluding rows Zj and (Cj –
Zj)) is either negative or zero.

26. UNBOUNDED SOLUTION
 Solve the given LP problem:
Maximize: Z = 10X1 + 20X2
Subject to:
2X1 + 4X2 ≥ 16
X1 + 5X2 ≥ 15
X1, X2 ≥ 0
Contribution Per Unit Cj 10 20 0 0 –M –M
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 A1 A2
–M A1 16 2 4 –1 0 1 0 16/4 = 4
–M A2 15 1 5* 0 –1 0 1 15/5 = 3 ←
Total Profit (Zj) –31M –3M –9M M M –M –M
Net Contribution (Cj – Zj) 10+3M 20+9M ↑ –M –M 0 0
Contribution Per Unit Cj 10 20 0 0 –M –M
Ratio
CBi
Basic
Variables (B)
Quantity
(Qty)
X1 X2 S1 S2 A1 A2
–M A1 4 (6/5)* 0 –1 4/5 1 –4/5 4/(6/5)=20/6 ←
20 X2 3 1/5 1 0 –1/5 0 1/5 3/(1/5)=15
Total Profit (Zj) 60–4M 4 – (6/5)M 20 M –4–(4/5)M –M 4M/5+4
Net Contribution (Cj – Zj) 6+(6/5)M ↑ 0 –M 4+(4/5)M 0 –9M/5–4

27. UNBOUNDED SOLUTION (Cont…)
Contribution Per Unit Cj 10 20 0 0 –M –M
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 A1 A2
10 X1 10/3 1 0 –(5/6) 2/3 5/6 –2/3 ---
20 X2 7/3 0 1 (1/6)* –1/3 –1/6 1/3 (7/3)/(1/6) = 14 ←
Total Profit (Zj) 80 10 20 –5 0 5 0
Net Contribution (Cj – Zj) 0 0 5 ↑ 0 –M–5 –M
Contribution Per Unit Cj 10 20 0 0 –M –M Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2 A1 A2
10 X1 15 1 5 0 –1 0 1 (Negative Value)
0 S2 14 0 6 1 –2 –1 2 (Negative Value)
Total Profit (Zj) 150 10 50 0 –10 0 10
Net Contribution (Cj – Zj) 0 –30 0 10 ↑ –M –M–10

28. MULTIPLE OPTIMAL SOLUTIONS
After the simplex method finds one optimal basic feasible
solution, you can detect other optimal basic feasible solutions
if there are any and find them as follows:
Whenever a problem has more than one optimal basic feasible
solution, at least one of the non–basic variables has a
coefficient of zero in the (Cj – Zj) row Zero (0), so increasing
any such variable will not change the value of the objective
function. Therefore, these other optimal basic feasible
solutions can be identified (if desired) by performing
additional iterations of the simplex method, each time
choosing a non–basic variable with Zero (0) coefficient as the
entering (incoming) variable.

29. MULTIPLE OPTIMAL SOLUTIONS
Maximize: Z = 2000X1 + 3000X2
Subject to:
6X1 + 9X2 ≤ 100
2X1 + X2 ≤ 20
X1, X2 ≥ 0
Max. Z = 2000X1 + 3000X2 + 0S1 + 0S2
Subject to:
2X1 + 4X2 + S1 = 16
X1 + 5X2 + S2 = 15
Contribution Per Unit Cj 2000 3000 0 0
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2
0 S1 100 6 9* 1 0 100/9 ←
0 S2 20 2 1 0 1 20/1
Total Profit (Zj) 0 0 0 0 0
Net Contribution (Cj – Zj) 2000 3000 ↑ 0 0
Contribution Per Unit Cj 2000 3000 0 0
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2
3000 X2 100/9 2/3 1 1/9 0 (100/9)/(2/3)=50/3
0 S2 80/9 (4/3)* 0 –1/9 1 (80/9)/(4/3)=20/3 ←
Total Profit (Zj) 100000/3 2000 3000 1000/3 0
Net Contribution (Cj – Zj) 0 ↑ 0 –1000/3 0
Since all the values in the above table of (Cj – Zj) ≤ 0; so, we having optimal solution. (X1 = 0,
X2 = 100/9, Zj = 100000/3).

30. MULTIPLE OPTIMAL SOLUTIONS
Contribution Per Unit Cj 2000 3000 0 0
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2 S1 S2
3000 X2 20/3 0 1 1/6 1/2
2000 X1 20/3 1 0 1/12 3/4
Total Profit (Zj) 100000/3 2000 3000 1000/3 0
Net Contribution (Cj – Zj) 0 0 –1000/3 0
So, the value of the objective function (Zj) = 100000/3; at
X1=20/3, X2=20/3

31. NON–EXISTING FEASIBLE / INFEASIBLE
SOLUTIONS
 The infeasibility (mean’s no feasible solutions
exist) condition occurs when the LP problem has
incompatible constraints. Science final simplex
table as shown optimal solution as all (Cj – Zj)
row elements are negative or zero. However,
observing the solution basis, if we find any
artificial variable is present as a basic variable
then the LP problem has infeasible solution.
Because the artificial variables have no meaning
therefore the values of the artificial variables
are totally meaningless.

32. NON–EXISTING FEASIBLE / INFEASIBLE SOLUTIONS
Solve the given LP problem using Two–Phase Simplex Method:
Maximize: Z = 5X1 + 3X2
Subject to:
2X1 + X2 ≤ 1
X1 + 4X2 ≥ 6
X1, X2 ≥ 0
Max. Z* = 0X1+0X2+0S1+0S2–A1
Subject to:
2X1+X2+S1 = 1
X1+4X2–S2+A1 = 6
X1, X2, S1, S2, A1 ≥ 0
Contribution Per Unit Cj 0 0 0 0 –1
Ratio
CBi Basic Variables (B)
Quantity
(Qty)
X1 X2 S1 S2 A1
0 S1 1 2 1* 1 0 0 1/1 = 1 ←
–1 A1 6 1 4 0 –1 1 6/4 = 3/2
Total Profit (Zj*) –6 –1 –4 0 1 –1
Net Contribution (Cj – Zj*) 1 4 ↑ 0 –1 0
Contribution Per Unit Cj 0 0 0 0 –1
CBi Basic Variables (B)
Quantity
(Qty)
X1 X2 S1 S2 A1
0 X2 1 2 1 1 0 0
–1 A1 2 –7 0 –4 –1 1
Total Profit (Zj*) –2 7 0 4 1 –1
Net Contribution (Cj – Zj*) –7 0 –4 –1 0
Since all the elements in the (Cj – Zj) row are negative or zero (≤ 0), so we are with optimal
solution but since ‘A1’ artificial variable appear as a basic variable, thus the above LP problem
does not have any feasible solution. In other words, the given LP problem has infeasible solution.

33. UNRESTRICTED–IN–SIGNED VARIABLES
 In the Simplex Method, we used the replacement ratio to determine the row in which the
entering (incoming) variable became a basic variable. Recall that the minimum non–negative
ratio in which we used to find the pivot (key) row that depended on the fact that any feasible
point required all variables to be non–negative. Thus, if some variables are allowed to be
unrestricted in sign then the minimum non–negative ratio may not be find therefore the
simplex algorithm are no longer valid.
 Thus, for each unrestricted in sign variable ‘Xi’, we begin by defining two new variables “Xi
/”
and “Xi
//”. Then substitute (Xi
/–Xi
//) for ‘Xi’ in each constraint and in the objective function.
Also add the sign restrictions “Xi
/ ≥ 0” and “Xi
// ≥ 0”.
 The effect of this substitution is to express ‘Xi’ as the difference of the two non–negative
variables “Xi
/” and “Xi
//”. Because all variables are now required to be non–negative, so we
can proceed with the simplex method. As we will soon see, no basic feasible solution can
have both “Xi
/ > 0” and “Xi
// > 0”. This means that for any basic feasible solution, each
unrestricted in sign variable ‘Xi’ must fall into one of the following three cases:
 Case–1: If (“Xi
/ > 0” and “Xi
// = 0”); this case occurs if a basic feasible solution has “Xi > 0”.
In this case, Xi = (Xi
/–Xi
//) = Xi
/. Thus, Xi = Xi
/.
– For Example; if Xi=5 in a basic feasible solution, this will be indicated by Xi
/ = 5 & Xi
// =
0.
 Case–2: If (“Xi
/ = 0” and “Xi
// > 0”); this case occurs if a basic feasible solution has “Xi < 0”.
Because Xi = (Xi
/–Xi
//) so we obtain Xi = “–Xi
//”.
– For Example; if Xi = –5 in a basic feasible solution, we will have Xi
/ = 0 & Xi
// = –5.
 Case–3: If (“Xi
/ = 0” and “Xi
// = 0”); in this case, Xi = 0 – 0 = 0.

34. UNRESTRICTED–IN–SIGNED VARIABLES
 A baker has ‘30’ gram flour and ‘5’ packets of yeast. Baking a loaf of bread requires ‘5’ gram
of flour and ‘1’ packet of yeast. Each loaf of bread can be sold for Rs. 30. The baker may
purchase additional flour at Rs. 4 per gram or sell leftover flour at the same price. Solve the
problem in such a way that helps the baker to maximize his profit.
SOLUTION:
Let ‘X1’ & ‘X2’ be the number of loaves of bread baked & number of grams of flour supply
increased.
Note: As ‘X2’ represents the number of grams of flour supply increased, therefore, if ‘X2 > 0’
means that ‘X2’ grams of flour were purchased while ‘X2 < 0’ means that ‘–X2’ grams of flour
were sold but if ‘X2 = 0’ means that no flour was bought or sold.
The complete LP model is:
Maximize: Z = 30X1 – 4X2
Subject to:
5 X1 ≤ 30 + X2  5X1 – X2 ≤ 30 (Flour constraint)
X1 ≤ 5 (Yeast Constraint)
X1 ≥ 0, X2 (Unrestricted in sign)
Because ‘X2’ is unrestricted in sign, so we substitute (X2
/ – X2
//) for ‘X2’ in the objective function and also in
the constraints. We get:
Maximize: Z = 30X1 – 4(X2
/ – X2
//)  30X1 – 4X2
/ + 4X2
//
Subject to:
5X1 – (X2
/ – X2
//) ≤ 30  5X1 – X2
/ + X2
// ≤ 30
X1 ≤ 5
X1, X2
/, X2
// ≥ 0

35. UNRESTRICTED–IN–SIGNED VARIABLES
After; introducing the slack variables S1, S2; Convert the given LP problem into standard form.
Maximize:Z = 30X1 – 4X2
/ + 4X2
// + 0S1 + 0S2
Subject to:
5X1 – X2
/ + X2
// +S1 = 30
X1 + S2 = 5
X1, X2
/, X2
//, S1, S2 ≥ 0
Contribution Per Unit Cj 30 –4 4 0 0
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2
/ X2
// S1 S2
0 S1 30 5 –1 1 1 0 6
0 S2 5 1* 0 0 0 1 5 ←
Total Profit (Zj) 0 0 0 0 0 0
Net Contribution (Cj – Zj) 30 ↑ –4 4 0 0
Contribution Per Unit Cj 30 –4 4 0 0
Ratio
CBi
Basic Variables
(B)
Quantity
(Qty)
X1 X2
/ X2
// S1 S2
0 S1 5 0 –1 1* 1 –5 5 ←
30 X1 5 1 0 0 0 1 ---
Total Profit (Zj) 150 30 0 0 0 30
Net Contribution (Cj – Zj) 0 –4 4 ↑ 0 –30

36. UNRESTRICTED–IN–SIGNED VARIABLES
Contribution Per Unit Cj 30 –4 4 0 0
CBi Basic Variables (B)
Quantity
(Qty)
X1 X2
/ X2
// S1 S2
4 X2
// 5 0 –1 1 1 –5
30 X1 5 1 0 0 0 1
Total Profit (Zj) 170 30 –4 4 4 10
Net Contribution (Cj – Zj) 0 0 0 –4 –10
Since all the values of (Cj – Zj) ≤ 0; so, the solution is optimal.
Value of ‘Z’ = (5)(4) + (5)(30) = 170
Optimal solution is 170 for Max. ‘Z’; at X1= 5, X2
// = 5, X2
/ = 0. As, X2 = (X2
/ –
X2
//) = (0 – 5) = –5;
means the baker should sell ‘5’ grams of flour. It is optimal for the baker to
sell flour, because having ‘5’ packets of yeast limit the baker to manufacturing
at most ‘5’ loaves of bread. These ‘5’ loaves of bread use (5)(5)=25 grams of
flour; so 30–25 = 5 grams of flour are left to sell.

37. FUNDAMENTAL THEOREM
OF LINEAR PROGRAMMING
37
 Every Linear Programming (LP) Problem is either
feasible, or unbounded, or infeasible.
 If it has a feasible solution then it has a basic
feasible solution.
 If it has an optimal solution then it is basic
feasible solution.

38. QUESTIONS