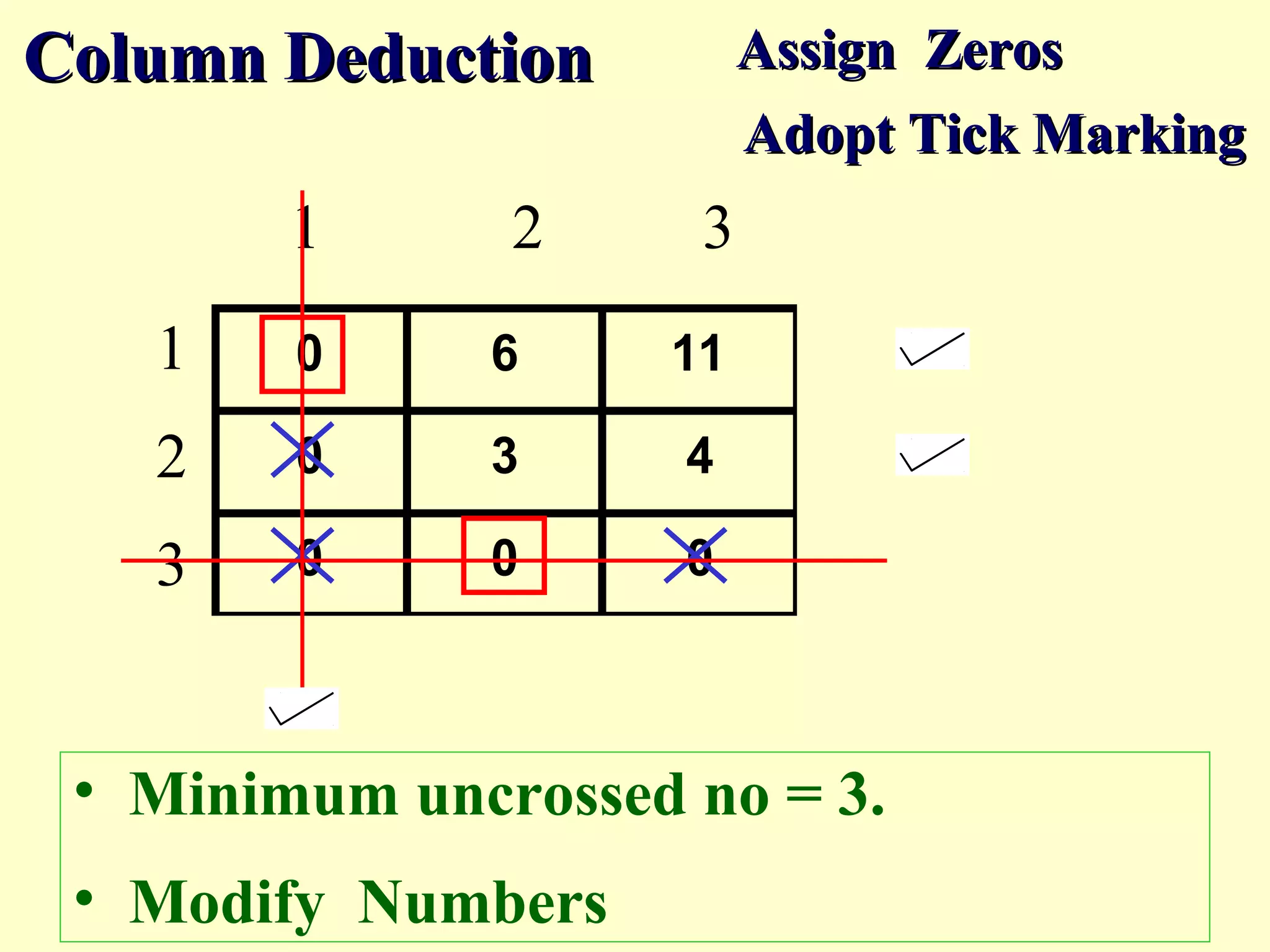
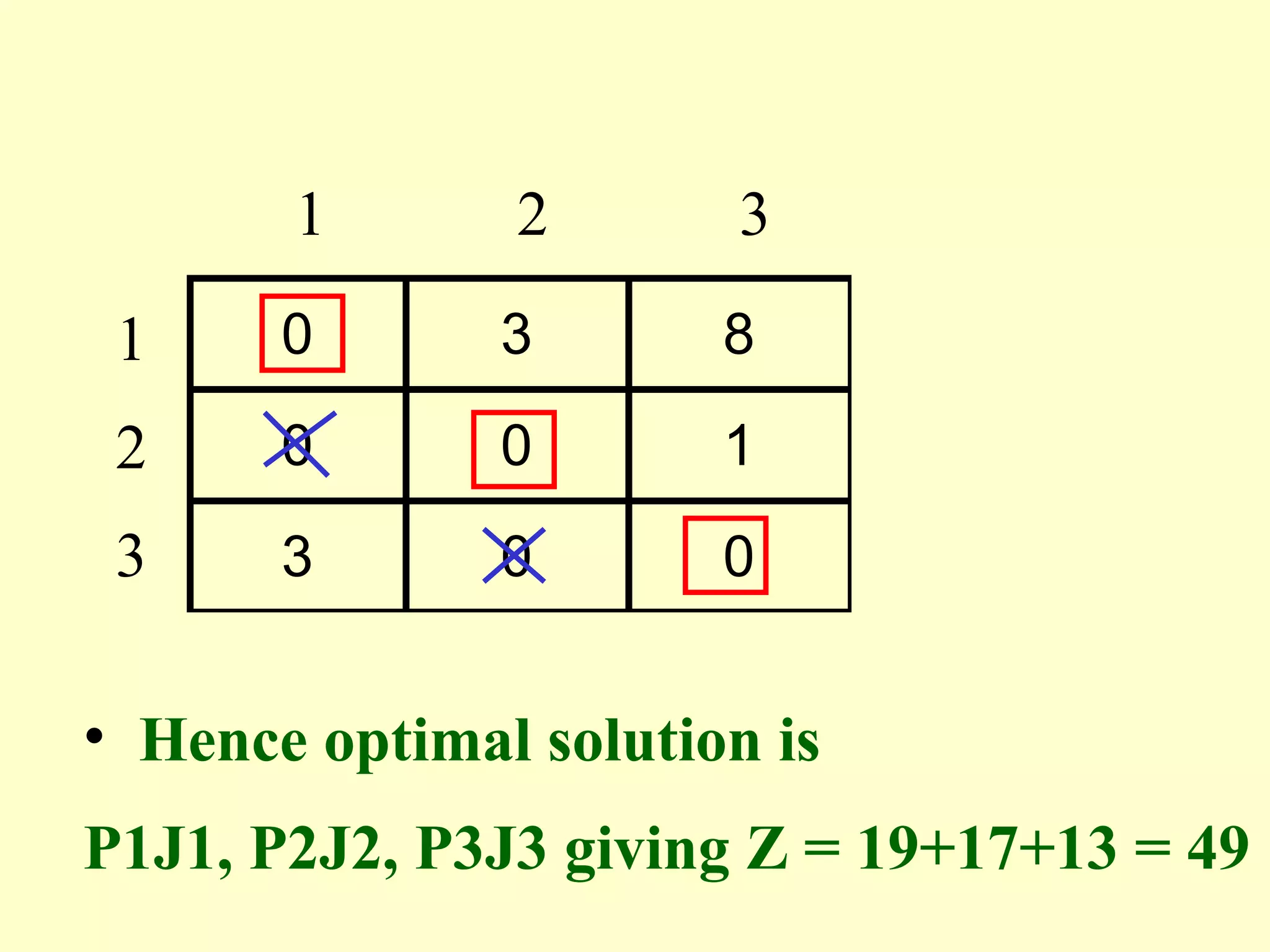
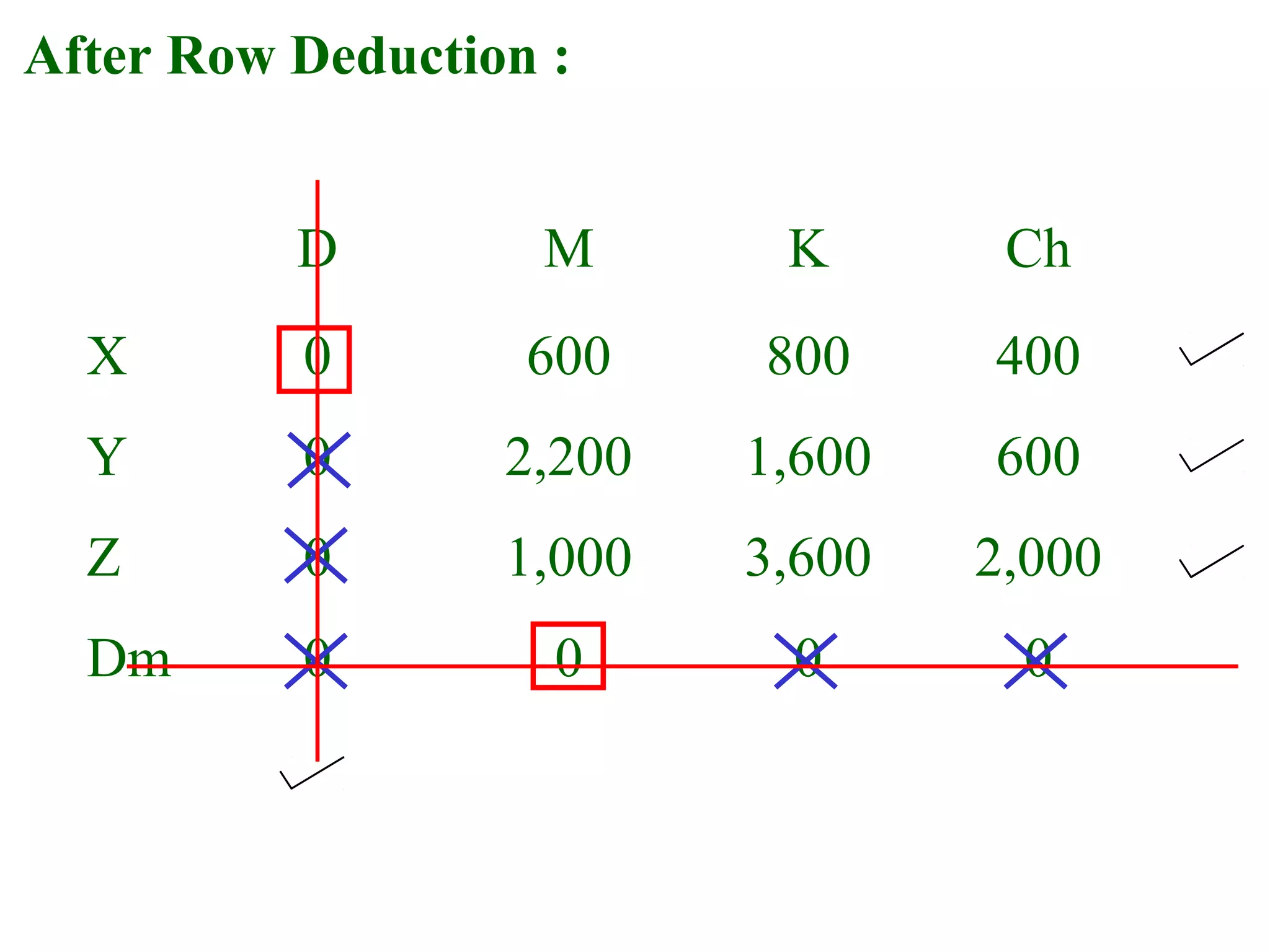
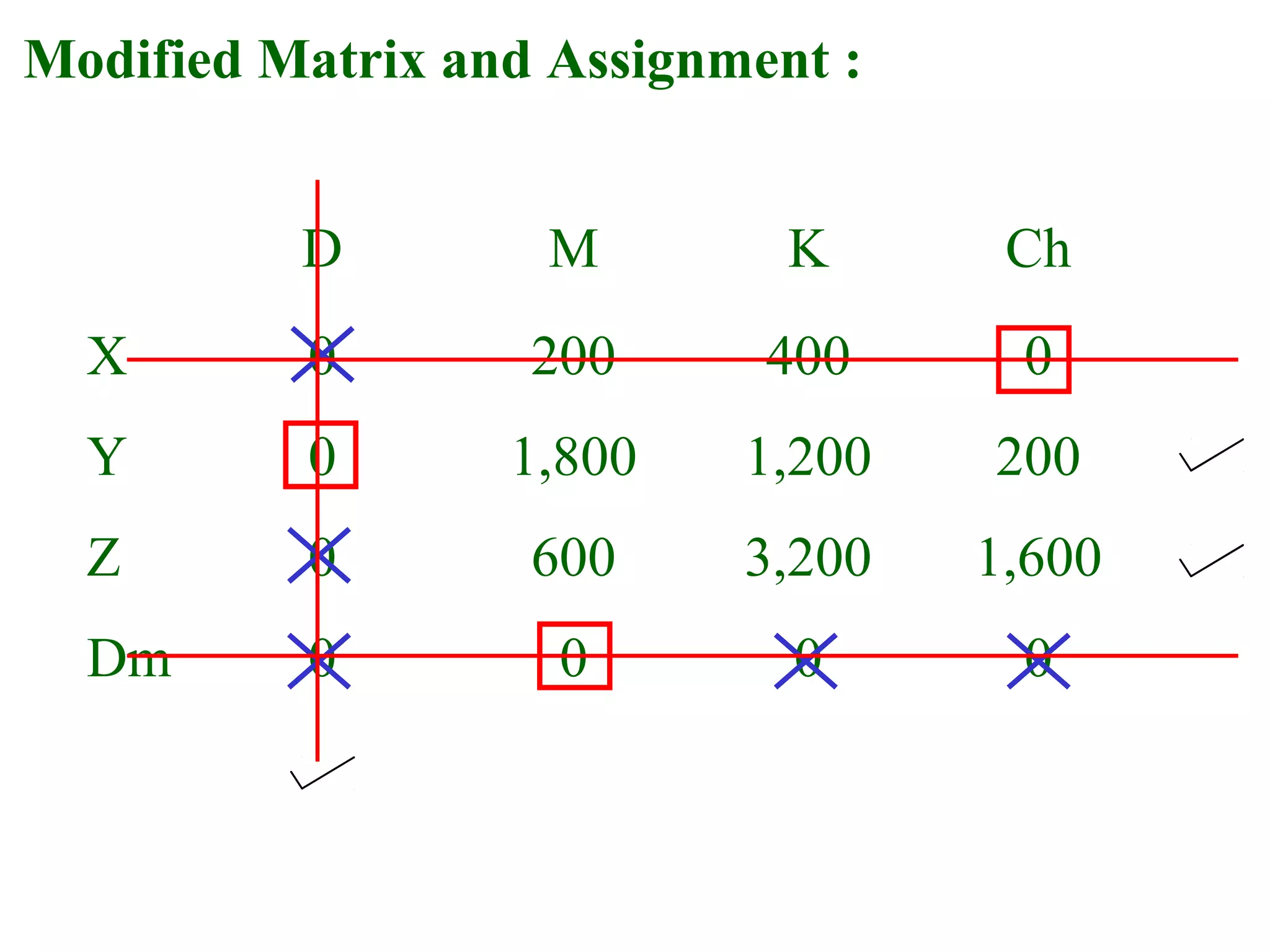
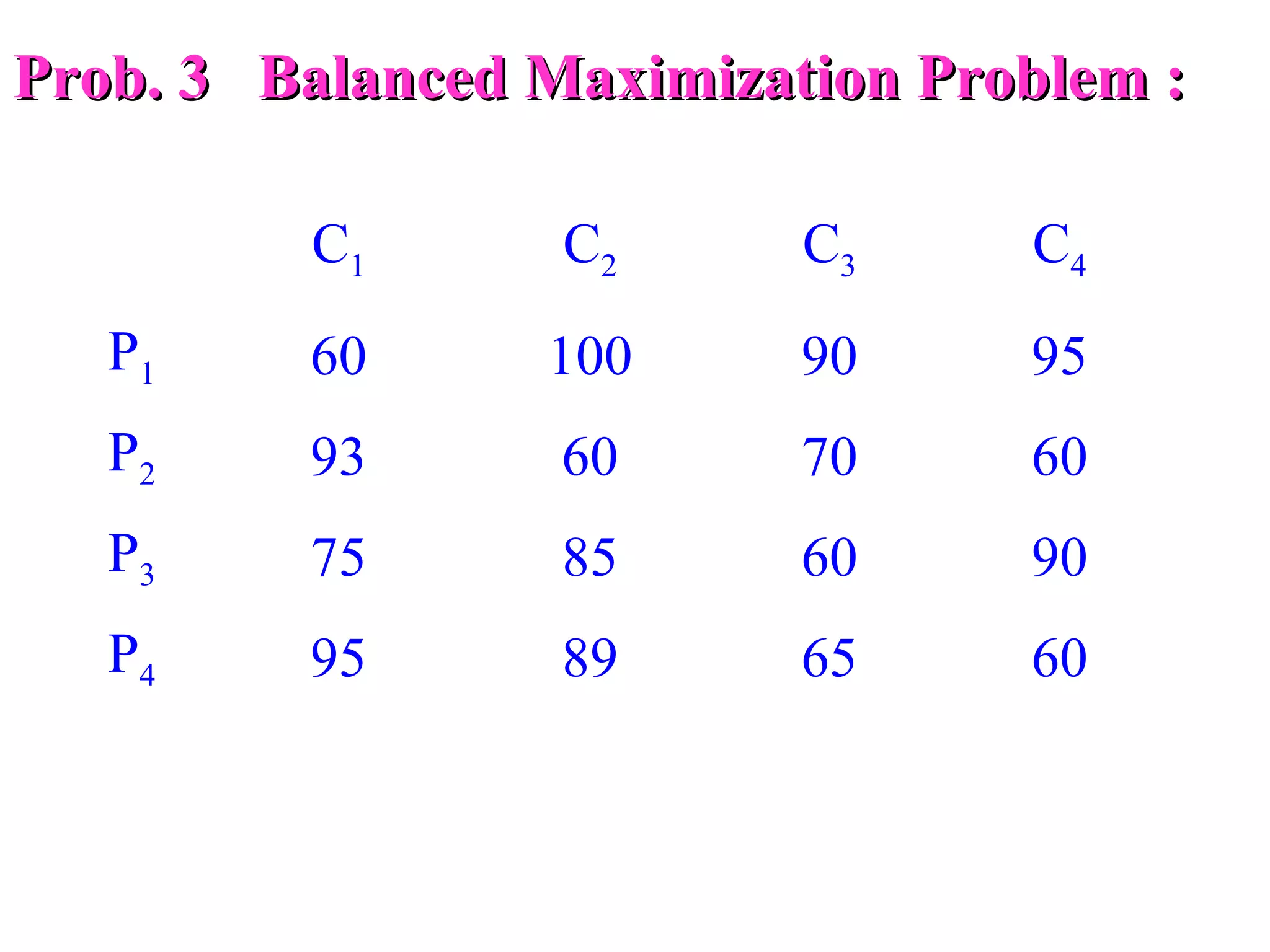
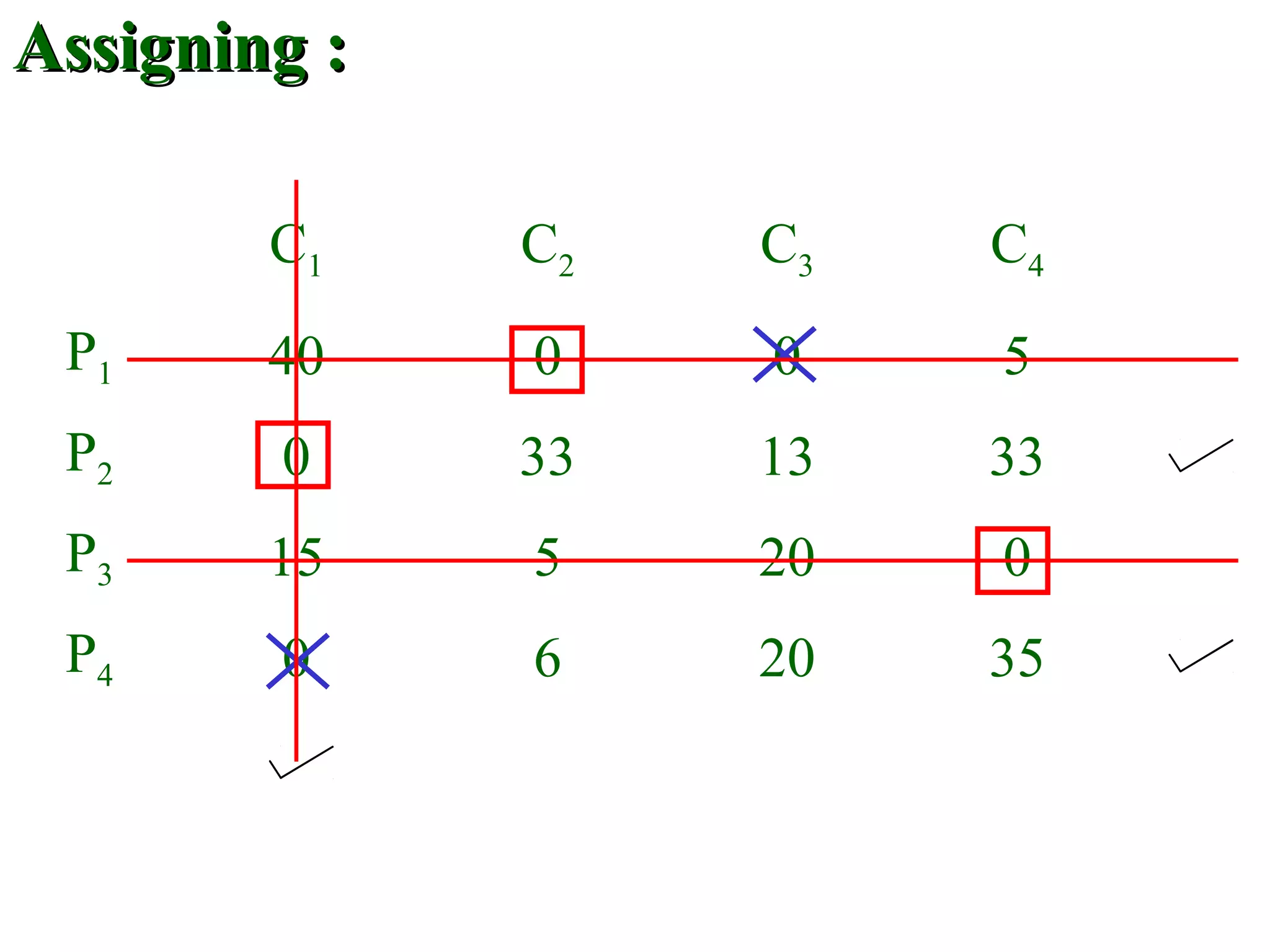
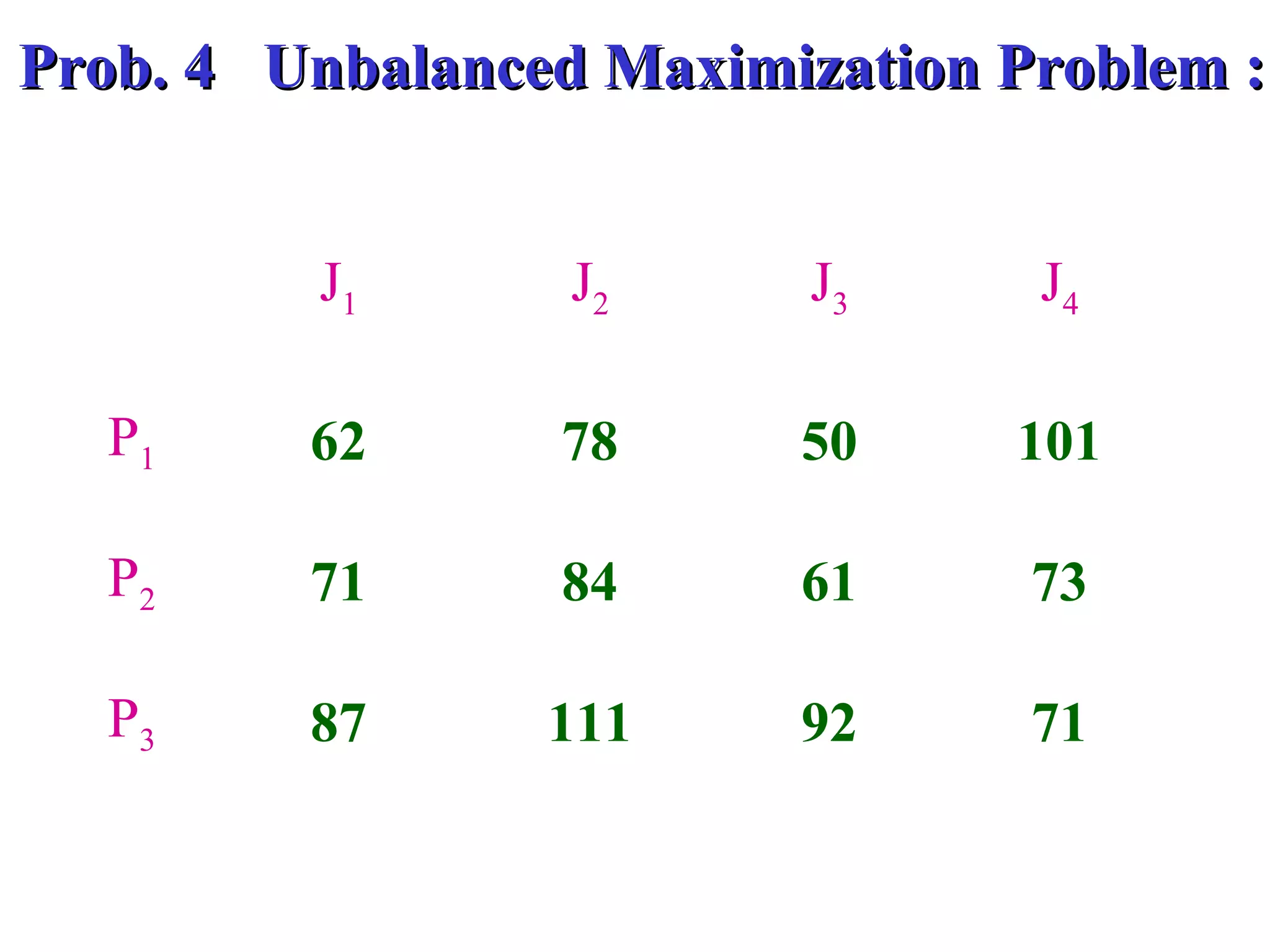
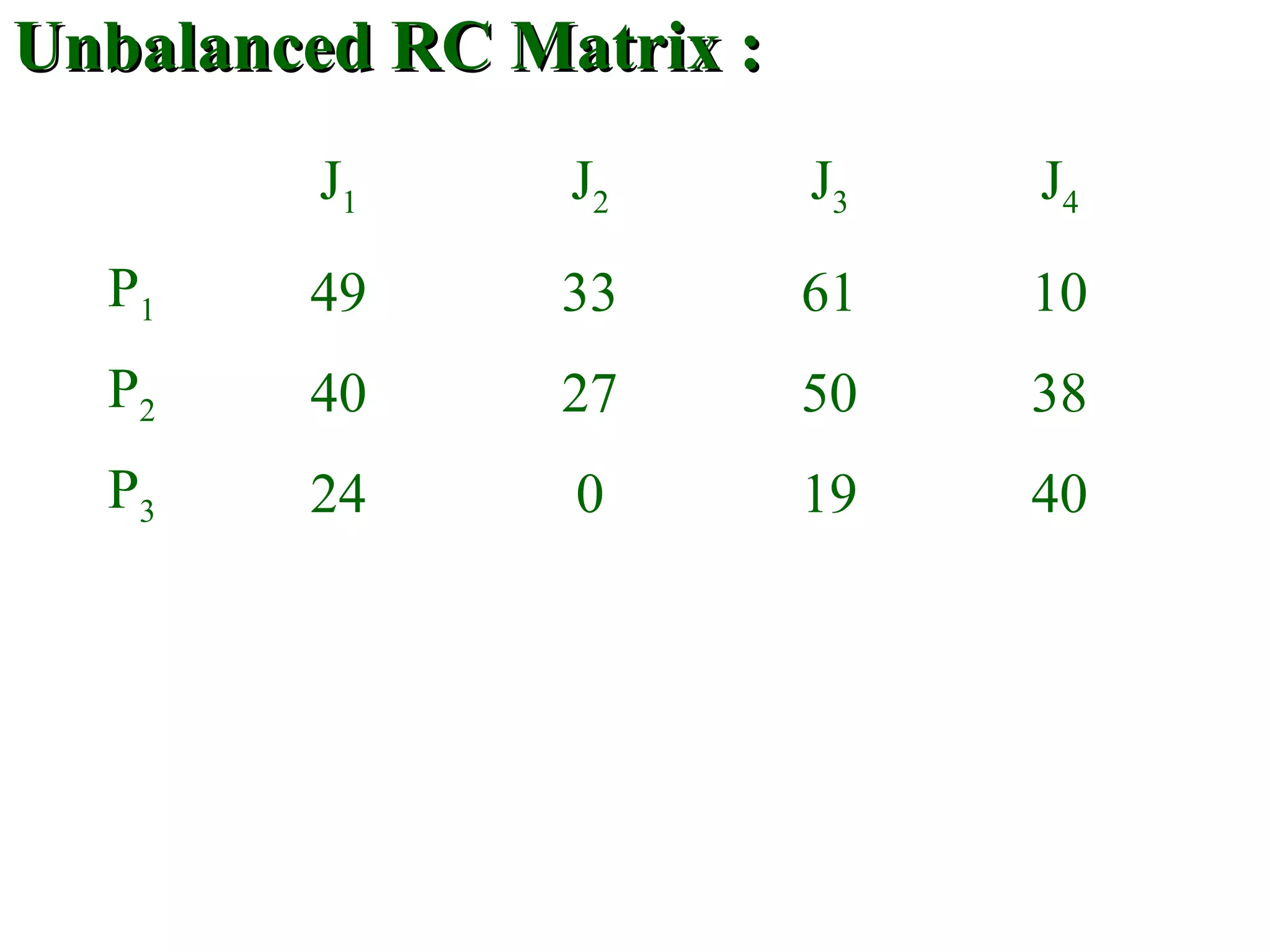
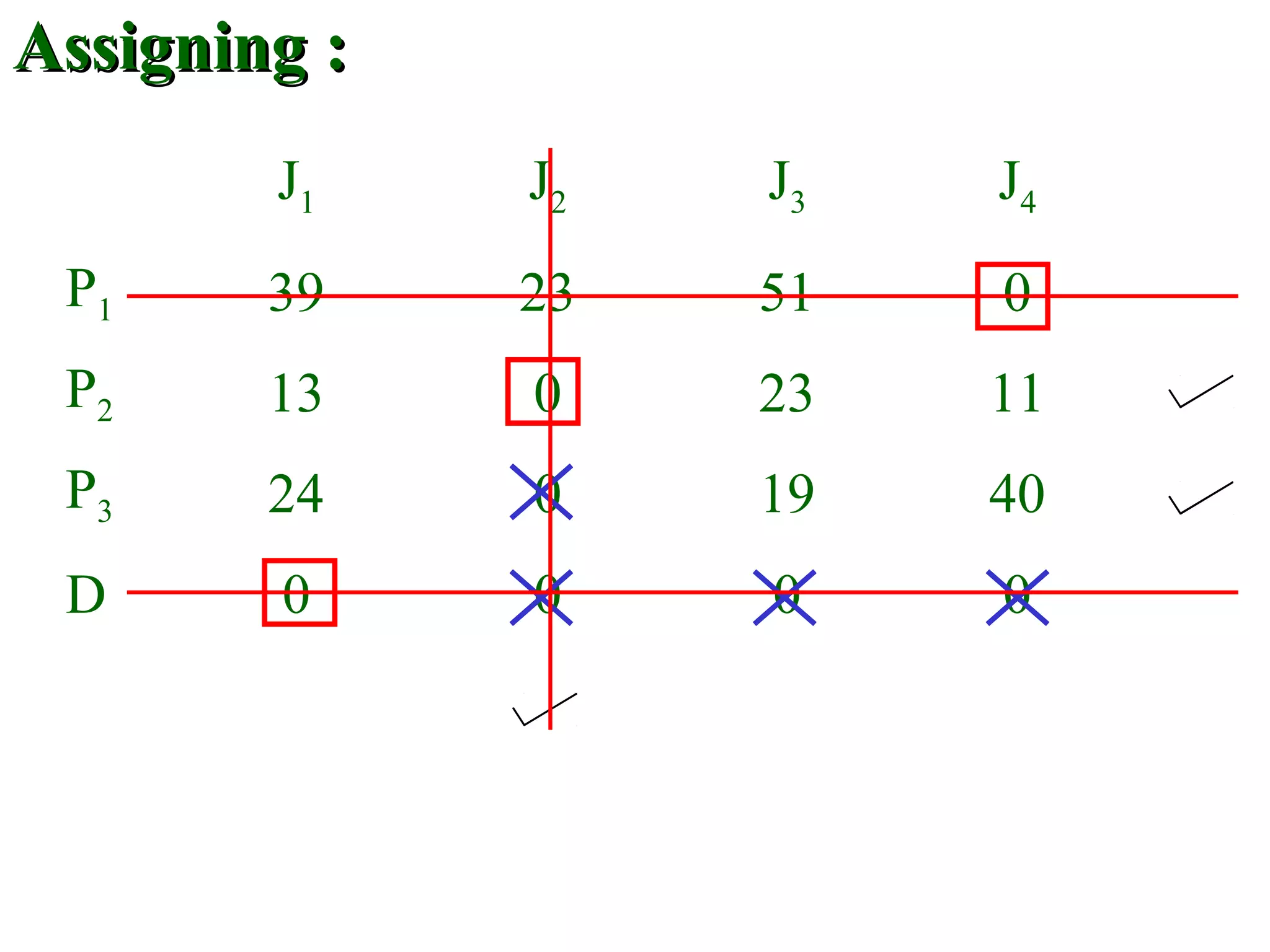
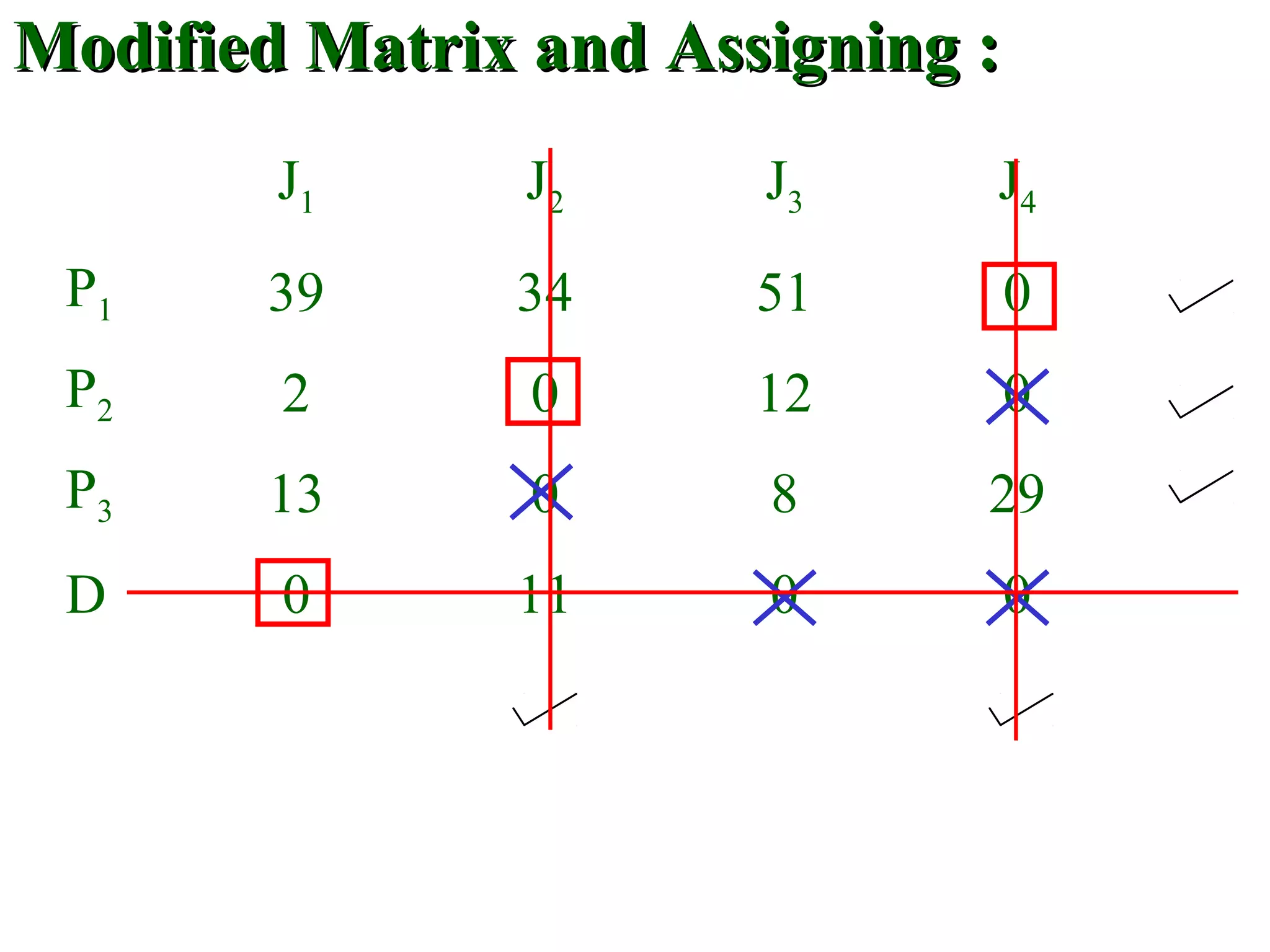
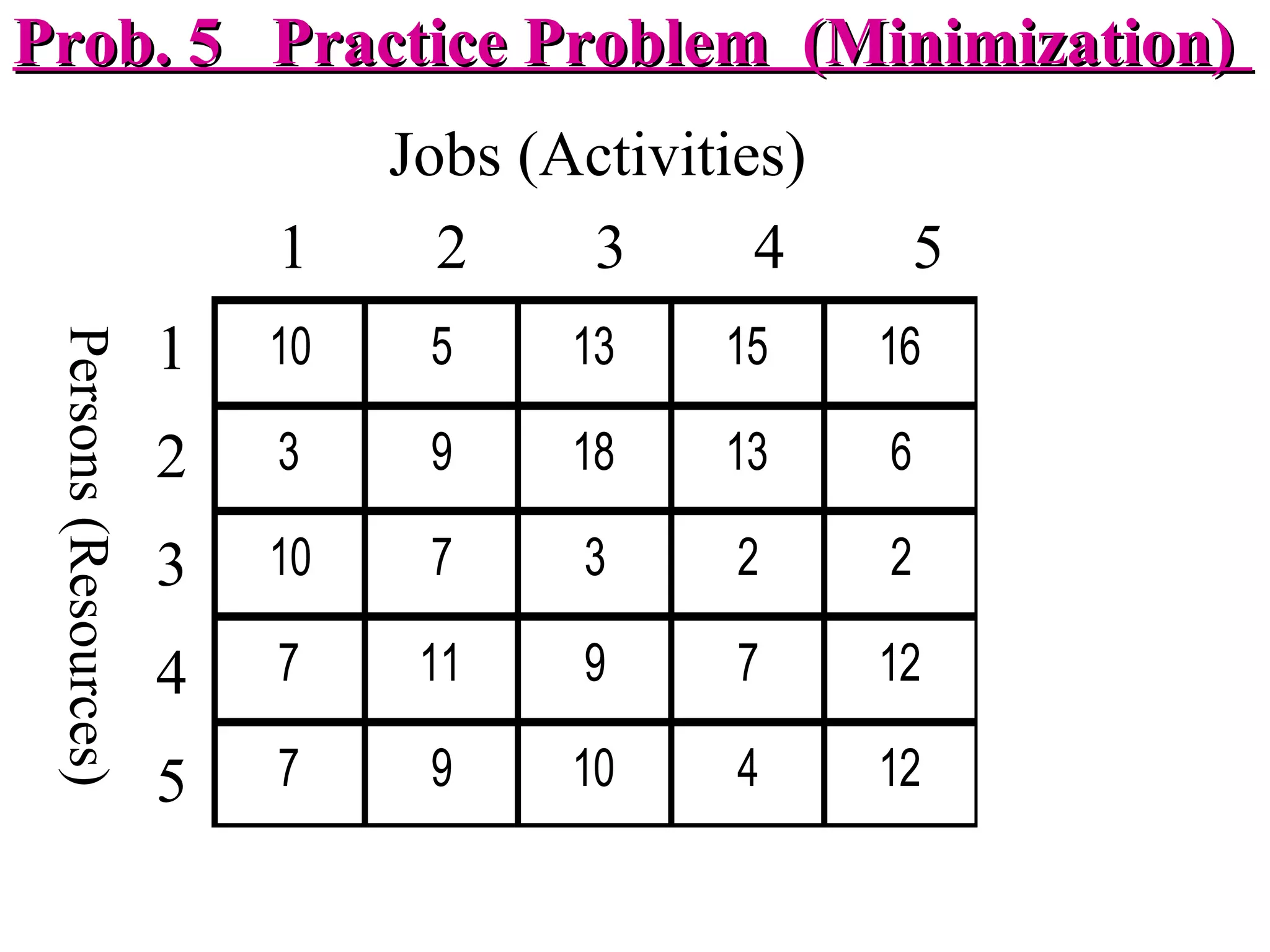
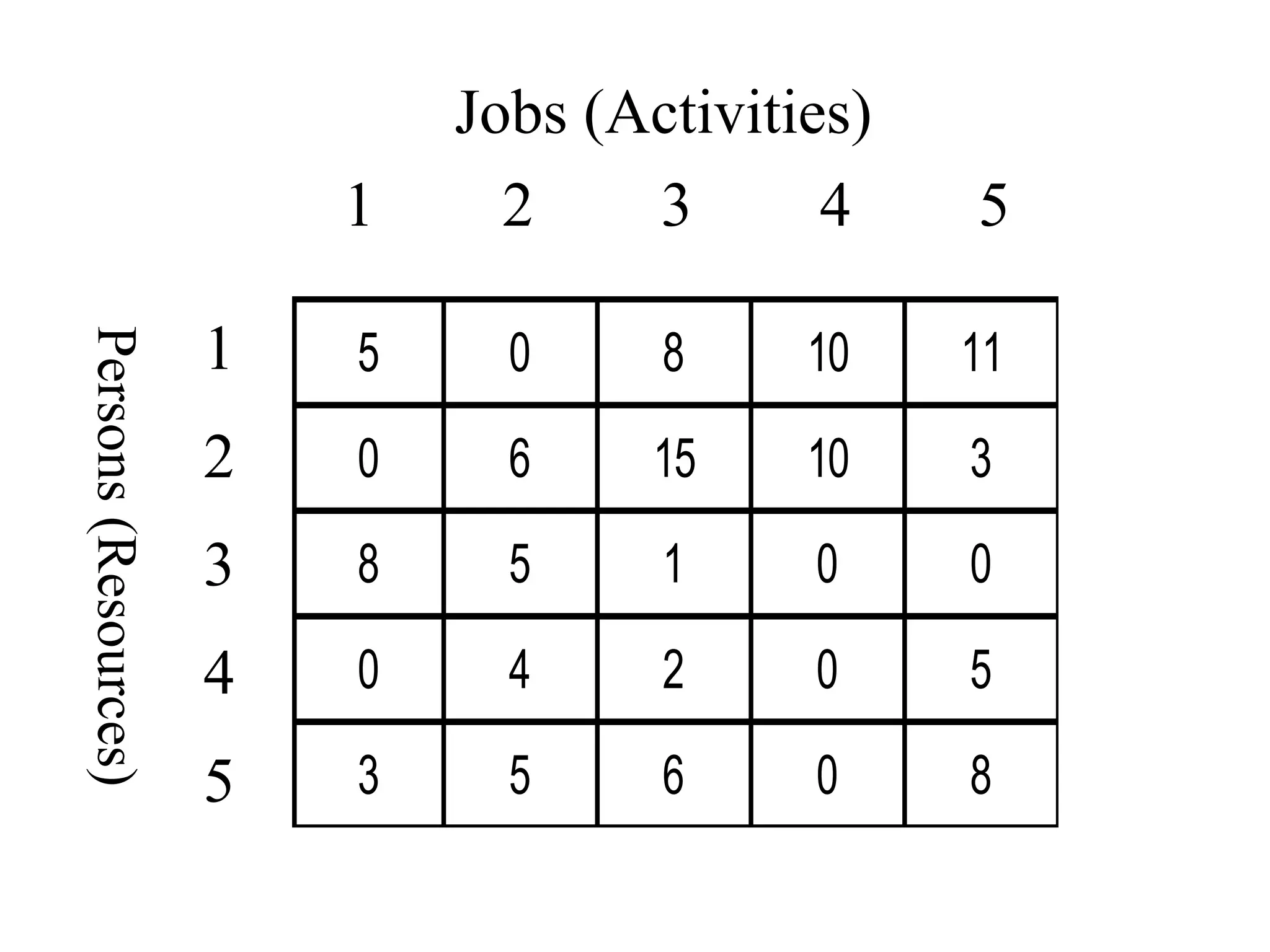
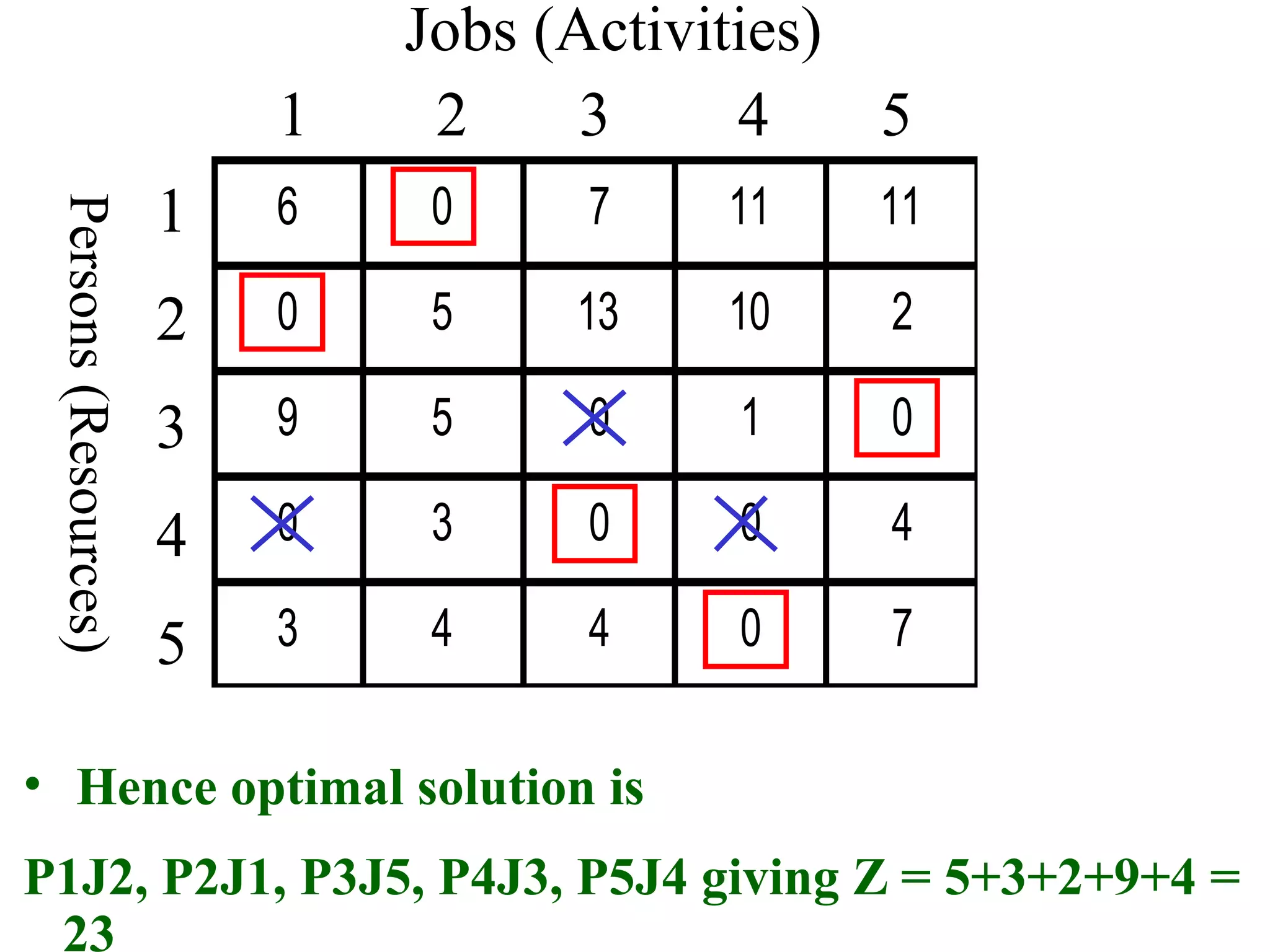
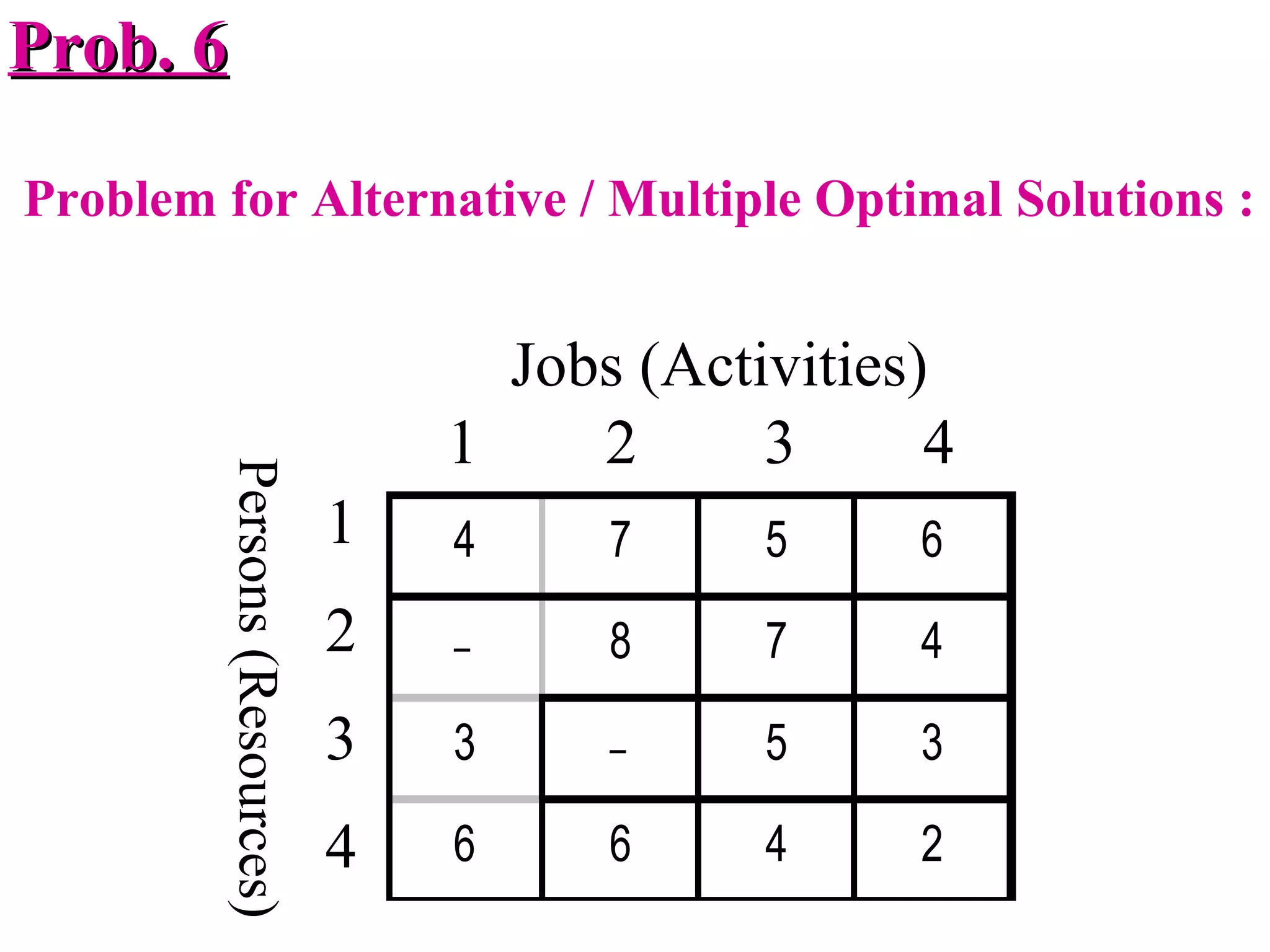
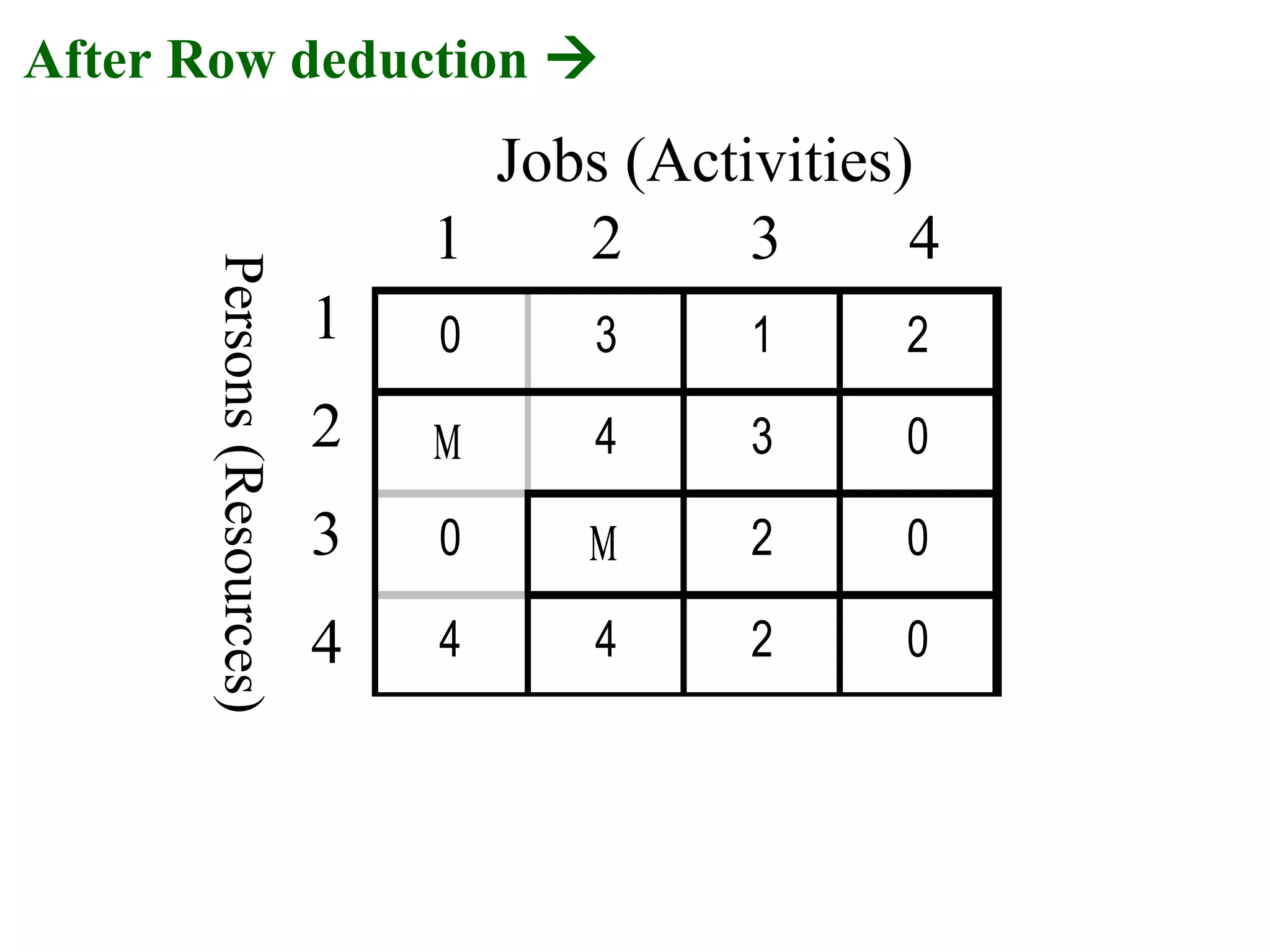
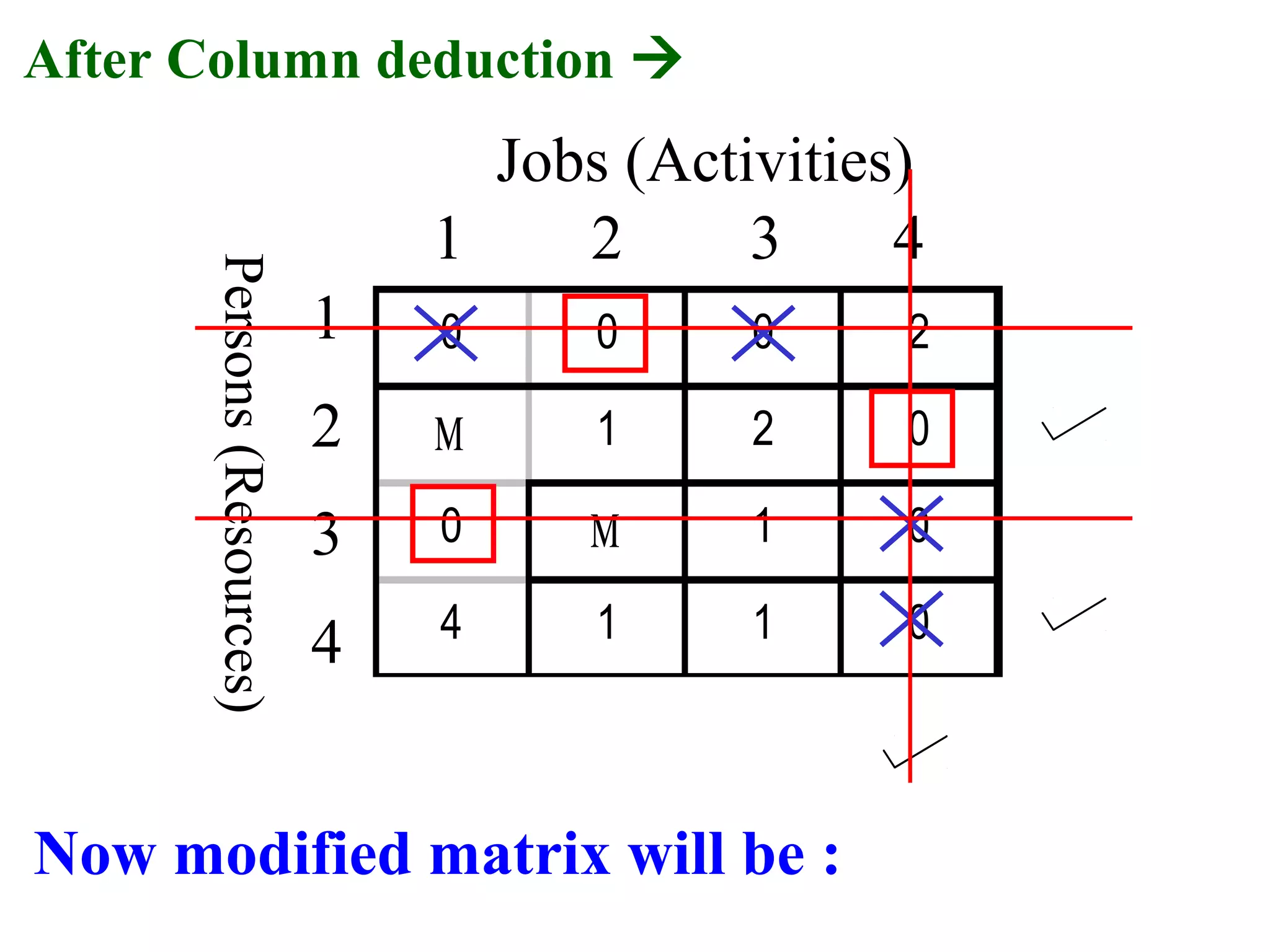
The document discusses different methods to solve assignment problems including enumeration, integer programming, transportation, and Hungarian methods. It provides examples of balanced and unbalanced minimization and maximization problems. The Hungarian method is described as having steps like row and column deduction, assigning zeros, and tick marking to find the optimal assignment with the minimum cost or maximum profit. A sample problem demonstrates converting a profit matrix to a relative cost matrix and using the Hungarian method to find the optimal solution.

1. • Methods to solve LPP :
1. Graphical Method - for only two variables.
2. Simplex Method - Universal method.
3. Assignment Method - Special method.
4. Transportation Method - Special method.
Note : Methods (2), (3) and (4) are iterative
methods.

2. Assignment Method
(Special Method)

3. • Assignment Problems
and
• Methods to solve such
problems

4. C11 C12 . . C1n
C21 C22 . . C2n
. . . . .
. . . . .
Cm1 . . . Cmn
Jobs (Activities)
1 2 . . n
1
2
.
.
m
Persons(Resources)
CasesCases
• m = n
• m ≠ n
• Cij
• Pij
• Cij = Cost associated with assigning ith
resource to jth
activity
Assignment ProblemAssignment Problem

5. A. Balanced Minimization → m = n with Cij
B. Unbalanced Minimization →m ≠ n with Cij
C. Balanced Maximization → m = n with Pij
D. Unbalanced Maximization →m ≠ n with Pij
Categories of Assignment ProblemsCategories of Assignment Problems

6. C11 C12 . . C1n
C21 C22 . . C2n
. . . . .
. . . . .
Cn1 . . . Cnn
Jobs (Activities)
1 2 . . n
1
2
.
.
n
Persons(Resources)
• Xij = assignment of ith
resource to jth
activity
• Assignments are made on one to one basis
A.A. Balanced Minimization ProblemBalanced Minimization Problem

7. Formulation of Assignment Problem as LPP
1 1
.
n n
i j
Min Z Cij Xij
= =
= ∑∑
1
/ 1 ( )
n
j
s t Xij for all i I
=
= −∑
1
1 ( )
n
i
Xij for all j II
=
= −∑
0 1 & .All Xij or for all i j=

8. Methods to solve Assignment ProblemsMethods to solve Assignment Problems
4. Hungarian Method
1. Enumeration Method
2. Integer Programming Method
3. Transportation Method

9. C11 C12
C21 C22
1 2
1
2
1.1. Enumeration MethodEnumeration Method
• For n x n Problem---- n!
2! (=2)• No. of Possible solutions =
• P1J1 , P2J2 OR P1J2 , P2J1
• For 4 x 4 Problem---- 4! = 24
• For 5 x 5 Problem----5! = 120

10. • All Xij = 0 or 1 → 0-1 Integer programming.
2.2. Integer Programming MethodInteger Programming Method
• Difficult to solve manually.
• For n x n Problem → Variables = n x n.
Constraints = n+n = 2n
• For 5 x 5 Problem → Variables = 25
Constraints = 10

11. • Formulate the problem in Transportation
Problem format.
3.3. Transportation MethodTransportation Method
C11 C12 . . C1n
C21 C22 . . C2n
. . . . .
. . . . .
Cn1 . . . Cnn
1 2 . . n
1
2
.
.
n
1
1
.
1
1 1 . . 1

12. 4.4. Hungarian MethodHungarian Method
1. Row Deduction
2. Column Deduction
3. Assign zeros-If all assignments are over,
Then STOP
Else Go To Step 4
4. Adopt Tick Marking Procedure
5. Modify Cij and Go To Step 3
(Mr. D. Konig - A Hungarian Mathematician)
Steps :Steps :

13. 1 2 3
1
2
3
Prob. 1Prob. 1 Balanced Minimization ProblemBalanced Minimization Problem
Perform Row DeductionPerform Row Deduction
19 28 31
11 17 16
12 15 13

14. 0 9 12
0 6 5
0 3 1
1 2 3
1
2
3
Row DeductionRow Deduction
• Perform Column DeductionPerform Column Deduction

15. 0 6 11
0 3 4
0 0 0
1 2 3
1
2
3
Column DeductionColumn Deduction
• Minimum uncrossed no = 3.
• Modify Numbers
Assign ZerosAssign Zeros
Adopt Tick MarkingAdopt Tick Marking

16. 0 3 8
0 0 1
3 0 0
1 2 3
1
2
3
• Hence optimal solution is
P1J1, P2J2, P3J3 giving Z = 19+17+13 = 49

17. Procedure of Assigning ZerosProcedure of Assigning Zeros
Steps to be followed, after getting at-least one zero in each row &
each column.
1. Start with 1st row. If there is only one uncrossed, unassigned
zero, assign it & cross other zeros in respective column (of
assigned zero), if they exits, else go to next row. Repeat this for
next all other rows.
2. If still uncrossed, unassigned zeros are available, start with first
column. If there is only one uncrossed, unassigned zero, assign it
and cross other zeros in respective row of assigned zero, if they
exit, else go to next column. Repeat this for next all other columns.
3. Repeat 1 & 2 until single uncrossed, unassigned zeros are
available, while going through rows & columns.
4. If still multiple uncrossed, unassigned zeros are available while
going through rows & columns, it indicates that multiple
(alternative) optimal solutions are possible.
Assign any one remaining uncrossed, unassigned zero & cross
remaining zeros in respective row & column of assigned zero.
Then go to 1.
5. If required assignments are completed then STOP, else perform
“Tick Marking Procedure”. Modify numbers & go to 1.

18. Tick marking ProcedureTick marking Procedure
(To draw minimum number of lines through zeros.)
1. Tick marks row/rows where there is no assigned zero.
2. Tick mark column/columns w.r.t. crossed zero/zeros in
marked row/rows.
3. Tick mark row/rows w.r.t. assigned zero in marked
column/columns.
4. Go to to step 2 and repeat the procedure until no zero is
available for tick marking.
Then
5. Draw lines through unmarked rows and marked columns
(Check no. of lines = No. of assigned
zeros)

19. Tick marking ProcedureTick marking Procedure
(Continue)(Continue)
How to Modify numbers ?
Find minimum number out of uncrossed numbers.
1. Add this minimum number to crossings.
2. Deduct this number from all uncrossed numbers one by one.
3. Keep crossed numbers, on horizontal & vertical lines,
except on crossing, same

20. C11 C12 C13
C21 C22 C23
. . .
. . .
C51 C52 C53
Jobs (Activities)
1 2 3
1
2
3
4
5
Persons(Resources)
• D1 and D2 Dummy Jobs are to be
introduced to balance the problem
B. Unbalanced Minimization ProblemB. Unbalanced Minimization Problem

21. C11 C12 C13 0 0
C21 C22 C23 0 0
. . . 0 0
. . . 0 0
C51 C52 C53 0 0
Jobs (Activities)
1 2 3 D1 D2
1
2
3
4
5
Persons(Resources)
• D1 and D2 are Dummy Jobs : Cij = 0

22. Prob. 2 The personnel manager of ABC Company wants
to assign Mr. X, Mr. Y and Mr. Z to regional offices. But the
firm also has an opening in its Chennai office and would send
one of the three to that branch, if it were more economical
than a move to Delhi, Mumbai or Kolkata. It will cost Rs.
2,000 to relocate Mr. X to Chennai, Rs. 1,600 to reallocate
Mr. Y there, and Rs. 3,000 to move Mr. Z. What is the
optimal assignment of personnel to offices ?
Office
Delhi Mumbai Kolkata
Personnel
Mr. X 1,600 2,200 2,400
Mr. Y 1,000 3,200 2,600
Mr. Z 1,000 2,000 4,600

23. UBMin (AP), after adding Chennai :
Delhi Mumbai Kolkata Chennai
Mr. X 1,600 2,200 2,400 2,000
Mr. Y 1,000 3,200 2,600 1,600
Mr. Z 1,000 2,000 4,600 3,000

24. BMin (AP), after adding Dummy Row
:
Delhi Mumbai Kolkata Chennai
Mr. X 1,600 2,200 2,400 2,000
Mr. Y 1,000 3,200 2,600 1,600
Mr. Z 1,000 2,000 4,600 3,000
Dummy 0 0 0 0

25. After Row Deduction :
D M K Ch
X 0 600 800 400
Y 0 2,200 1,600 600
Z 0 1,000 3,600 2,000
Dm 0 0 0 0

26. Modified Matrix and Assignment :
D M K Ch
X 0 200 400 0
Y 0 1,800 1,200 200
Z 0 600 3,200 1,600
Dm 0 0 0 0

27. Modified Matrix and Assignment :
D M K Ch
X 200 200 400 0
Y 0 1,600 1,000 0
Z 0 400 3,000 1,400
Dm 400 0 0 0

28. Modified Matrix and Assignment :
D M K Ch
X 200 0 200 0
Y 0 1,400 800 0
Z 0 200 2,800 1,400
Dm 6 00 0 0 200
Hence, Optimal Solution is : XM, YCh, ZD
Giving Z = 2,200 + 1,600 + 1,000 = 4,800
Hence, it is economical to move Y to Chennai

29. Jobs (Activities)
1 2 3 4 5
1
2
3
4
5
Persons(Resources)
• Convert Profit Matrix into Relative Cost
Matrix
C. Balanced Maximization ProblemC. Balanced Maximization Problem
Pij

30. • How to Convert Profit Matrix into
Relative Cost Matrix ?
3. (Pij)max - Pij = RCij
1. (Pij) (-1) = RCij
2. 1/Pij = RCij

31. Prob. 3 Balanced Maximization Problem :Prob. 3 Balanced Maximization Problem :
C1 C2 C3 C4
P1 60 100 90 95
P2 93 60 70 60
P3 75 85 60 90
P4 95 89 65 60

32. Balanced RC Matrix :Balanced RC Matrix :
C1 C2 C3 C4
P1 40 0 10 5
P2 7 40 30 40
P3 25 15 40 10
P4 5 11 35 40

33. After Row Deduction :After Row Deduction :
C1 C2 C3 C4
P1 40 0 10 5
P2 0 33 23 33
P3 15 5 30 0
P4 0 6 30 35

34. After Column Deduction :After Column Deduction :
C1 C2 C3 C4
P1 40 0 0 5
P2 0 33 13 33
P3 15 5 20 0
P4 0 6 20 35

35. Assigning :Assigning :
C1 C2 C3 C4
P1 40 0 0 5
P2 0 33 13 33
P3 15 5 20 0
P4 0 6 20 35

36. Modified Matrix and Assigning :Modified Matrix and Assigning :
C1 C2 C3 C4
P1 46 0 0 5
P2 0 27 7 27
P3 21 5 20 0
P4 0 0 14 29
Hence, Optimal Solution is : P1C3, P2C1, P3C4, P4C2
Giving Z = 90 + 93 + 90 + 89 = 362

37. Jobs (Activities)
1 2 3
1
2
3
4
5
Persons(Resources)
• Convert Unbalanced Profit Matrix into
Unbalanced Relative Cost Matrix
D. Unbalanced Maximization ProblemD. Unbalanced Maximization Problem
Pij
• Then Balance the matrix and solve

38. Prob. 4 Unbalanced Maximization Problem :Prob. 4 Unbalanced Maximization Problem :
J1 J2 J3 J4
P1 62 78 50 101
P2 71 84 61 73
P3 87 111 92 71

39. Unbalanced RC Matrix :Unbalanced RC Matrix :
J1 J2 J3 J4
P1 49 33 61 10
P2 40 27 50 38
P3 24 0 19 40

40. Balanced RC Matrix :Balanced RC Matrix :
J1 J2 J3 J4
P1 49 33 61 10
P2 40 27 50 38
P3 24 0 19 40
D 0 0 0 0

41. After Row Deduction :After Row Deduction :
J1 J2 J3 J4
P1 39 23 51 0
P2 13 0 23 11
P3 24 0 19 40
D 0 0 0 0

42. Assigning :Assigning :
J1 J2 J3 J4
P1 39 23 51 0
P2 13 0 23 11
P3 24 0 19 40
D 0 0 0 0

43. Modified Matrix and Assigning :Modified Matrix and Assigning :
J1 J2 J3 J4
P1 39 34 51 0
P2 2 0 12 0
P3 13 0 8 29
D 0 11 0 0

44. Modified Matrix and Assigning :Modified Matrix and Assigning :
J1 J2 J3 J4
P1 37 34 49 0
P2 0 0 10 0
P3 11 0 6 29
D 0 13 0 2
Hence, Optimal Solution is : P1J4, P2J1, P3J2
Giving Z = 101 + 71 + 111 = 283

45. 10 5 13 15 16
3 9 18 13 6
10 7 3 2 2
7 11 9 7 12
7 9 10 4 12
Jobs (Activities)
1 2 3 4 5
1
2
3
4
5
Persons(Resources)Prob. 5 Practice Problem (Minimization)Prob. 5 Practice Problem (Minimization)

46. 5 0 8 10 11
0 6 15 10 3
8 5 1 0 0
0 4 2 0 5
3 5 6 0 8
Jobs (Activities)
1 2 3 4 5
1
2
3
4
5
Persons(Resources)

47. 5 0 7 10 11
0 6 14 10 3
8 5 0 0 0
0 4 1 0 5
3 5 5 0 8
Jobs (Activities)
1 2 3 4 5
1
2
3
4
5
Persons(Resources) • Minimum uncrossed Number = 1.

48. 6 0 7 11 11
0 5 13 10 2
9 5 0 1 0
0 3 0 0 4
3 4 4 0 7
Jobs (Activities)
1 2 3 4 5
1
2
3
4
5
Persons(Resources)
• Hence optimal solution is
P1J2, P2J1, P3J5, P4J3, P5J4 giving Z = 5+3+2+9+4 =
23

49. 4 7 5 6
− 8 7 4
3 − 5 3
6 6 4 2
Jobs (Activities)
1 2 3 4
1
2
3
4
Persons(Resources)
Prob. 6Prob. 6
Problem for Alternative / Multiple Optimal Solutions :

50. 0 3 1 2
Μ 4 3 0
0 Μ 2 0
4 4 2 0
Jobs (Activities)
1 2 3 4
1
2
3
4
Persons(Resources)
After Row deduction 

51. 0 0 0 2
Μ 1 2 0
0 Μ 1 0
4 1 1 0
Jobs (Activities)
1 2 3 4
1
2
3
4
Persons(Resources)
After Column deduction 
Now modified matrix will be :

52. 0 0 0 3
Μ 0 1 0
0 Μ 1 1
3 0 0 0
Jobs (Activities)
1 2 3 4
1
2
3
4
Persons(Resources)
• Hence, this is a case of alternative optimal solutions.
• Assign any one remaining zero and cross existing zeros
in respective row and column, then apply assigning
procedure.
• Hence, one of the optimal solutions is P1J2, P2J4, P3J1,
P4J3 giving Z = 7+4+3+4 = 18

53. 0 0 0 3
Μ 0 1 0
0 Μ 1 1
3 0 0 0
Jobs (Activities)
1 2 3 4
1
2
3
4
Persons(Resources)
• Hence, another optimal solution is P1J3, P2J2, P3J1,
P4J4 giving Z = 5+8+3+2 = 18
To get another optimal solution, assign another remaining zero.
P1J3 can not be assigned, as it is already assigned before.

54. . Restriction in Assignment.
e.g. Assignment of P3 to J4 is not possible.
Then C34 = M (Big Number)
. Alternative Optimal Solution Possibility
-Already considered.
. Particular assignment is prefixed.
e.g. If P3 & J4 prefixed
Then Row3 & Column4 are deleted.
Typical Cases in Assignment ProblemsTypical Cases in Assignment Problems

55. Typical
Questions

56. Que. Answer each of the following questions in brief.
[ 1 ] What are the methods to solve Assignment Problems ?
Ans. : (1) Enumeration Method
(2) Integer Programming Method
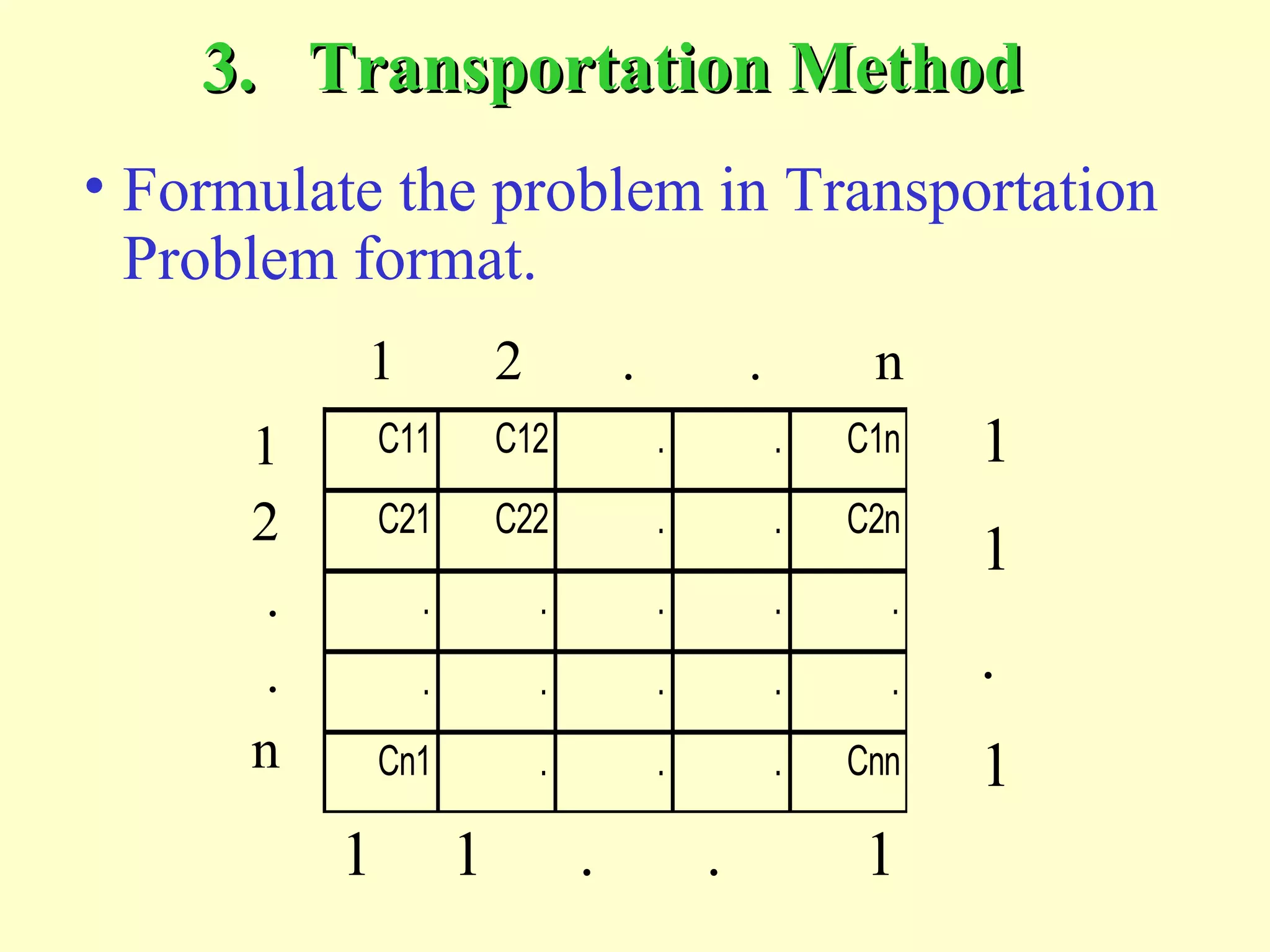
(3) Transportation Method
(4) Hungarian Method
[ 2 ] How can you identify a function as Linear ?
Ans. : Power of each variable = only 1.
No multiplication of variables.

57. [ 3 ] What is the purpose of “Tick Marking Procedure” in a
method of solving Assignment Problems ?
Ans. : The purpose of “Tick Marking” procedure is to
draw minimum number of lines covering zeros.
[ 4 ] What is significance of name “Hungarian Method” ?
Ans. : It is because of D. Konig of Hungary.

58. [ 5 ] Following is Minimization Assignment Problem.
(i) Write objective equation.
(ii) Write all possible constraints.
(iii) State “Non-Negativity” conditions for this problem.
(iv) State Optimal Solution. Is it unique optimal ?
X Y
A 3 2
B 4 5
Ans. : ( i ) Min Z = 3x11 + 2x12 + 4x21 + 5x22
( ii ) x11 + x12 = 1
x21 + x22 = 1
x11 + x21 = 1
x12 + x22 = 1
( iii ) All xij = 0 or 1 OR x11, x12, x21, x22 = 0 or 1
( iv ) Optimal solution is AY, BX giving Z = 6 (unique)

59. [ 6 ] Get Optimal Solution of following Minimization
Assignment Problem. How many Optimal Solutions are
existing for this problem ?
X Y Z
A 3 2 2
B 6 5 5
C 6 1 1
X Y Z
A 3 2 2
B 6 5 5
C 6 1 1
X Y Z
A 1 0 0
B 1 0 0
C 5 0 0

60. X Y Z
A 0 0 0
B 0 0 0
C 4 0 0
X Y Z
A 0 0 0
B 0 0 0
C 4 0 0
X Y Z
A 0 0 0
B 0 0 0
C 4 0 0
X Y Z
A 0 0 0
B 0 0 0
C 4 0 0
There are 4 Optimal Solutions.

61. RecapitulateRecapitulate
• Methods to solve Assignment
Problem
• Hungarian Method
• Typical cases of Assignment
Problems

62. Home Assignments :

63. [ 1 ] Answer the following in brief :
( a ) What is the purpose of “Tick Marking”
procedure in solving Assignment Problem ?
( b ) What is significance of name “Hungarian”
method ?

64. [ 2 ] For the following Minimization Assignment
Problem, answer the question given below.
J1
J2
J3
P1 2 4 3
P2 5 6 6
( a ) Formulate this problem as LPP.
( b ) Get all possible Optimal Solutions.

65. [ 3 ] ( i ) State possible methods of solving
“Assignment Problem”.
( ii ) State possible methods of converting
“Profit Matrix” into “Relative Cost Matrix”.
[ 4 ] Formulate following Assignment Problem as :
( i ) LPP
( ii ) Transportation Problem
P Q
A 2 5
B 6 4

66. [ 5 ] Find optimal assignments for following
“Minimization Assignment Problem”.
J1
J2
J3
P1 −10 −10 −12
P2 −18 −6 −14
P3 −6 −2 −2

67. [ 6 ] Average time taken by operators on 4 old
machines and a new machine are tabulated below.
Management is considering to replace one of the old
machines by a new machine. Is it advantageous to
replace new machine with an old machine ? Why ?
M1
M2
M3
M4 New
O1 10 12 8 10 11
O2 9 10 8 7 10
O3 8 7 8 8 8
O4 12 13 14 14 11

68. [ 7 ] Consider the problem of assigning four operators
to four machines. The assignment costs are given
in Rupees. Operator 1 cannot be assigned to
machine 3. Also operator 3 cannot be assigned to
machine 4. Find the optimal assignment.
M1 M2 M3 M4
1 5 5 − 2
2 7 4 2 3
3 9 3 5 −
4 7 2 6 7
If 5th Machine is made available and the
respective costs to the four operators are Rs. 2, 1,
2 and 8. Find whether it is economical to replace
any of the four existing machines. If so, which ?

69. [ 8 ] There are four batsman P, Q, R, & S. The
batsman are to be selected for first three
positions P1, P2 and P3. The expected score by
these batsman at three different positions are
given as below. Decide the optimal batsman for
these three positions.
P1
P2
P3
P 42 16 27
Q 48 40 25
R 50 18 36
S 58 38 60

70. [ 9 ]
J1 J2 J3 J4
P1 20 22 28 15
P2 16 20 12 13
P3 19 23 14 25
P4 10 16 12 10
Minimization Problem :

71. [ 10 ]
J1 J2 J3 J4
P1 10 24 30 15
P2 16 22 28 12
P3 12 20 32 10
P4 9 26 34 16
Minimization Problem :

72. Thank youThank you
For any Query or suggestion :
Contact :
Dr. D. B. Naik
Professor & Head, Training & Placement (T&P)
S. V. National Institute of Technology (SVNIT),
Ichchhanath, Surat – 395 007 (Gujarat) INDIA.
Email ID : dbnaik@gmail.com
dbnaik@svnit.ac.in
dbnaik_svr@yahoo.com
Phone No. : 0261-2201540 (D), 2255225 (O)