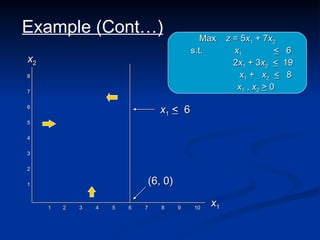
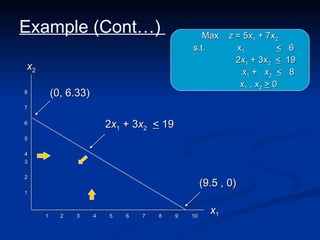
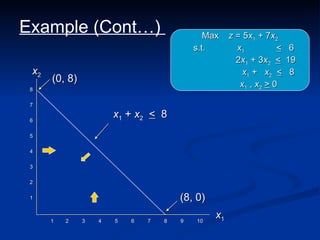
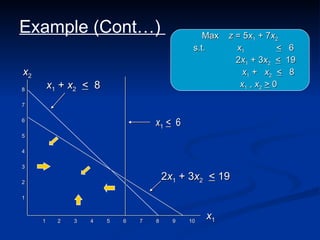
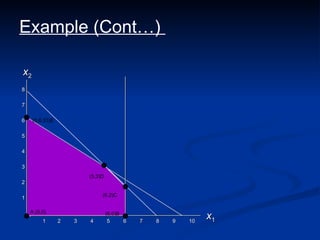
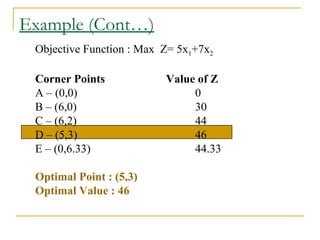
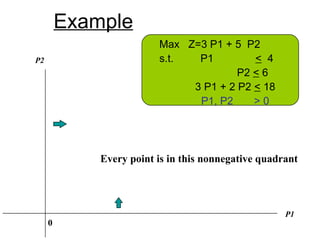
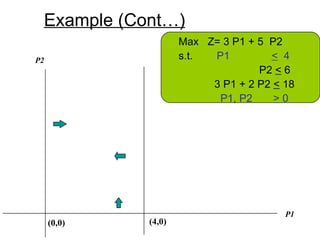
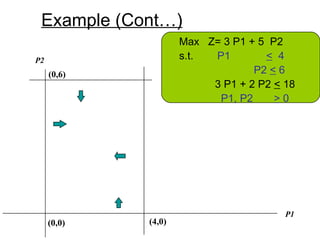
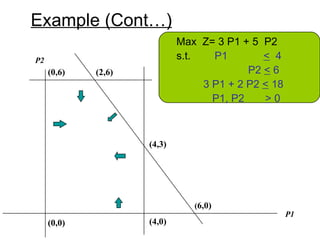
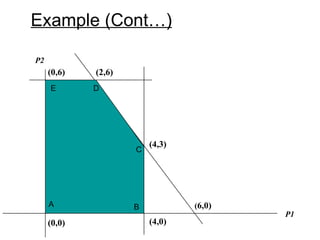
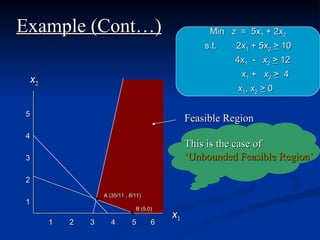
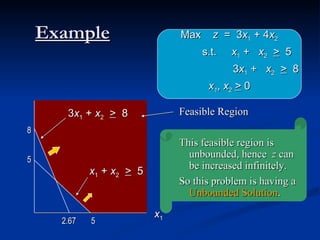
The document describes the graphical method for solving linear programming problems with two decision variables. It provides the step-by-step procedure which involves plotting the constraints on a graph to identify the feasible region, determining the corner points of this region which represent the feasible solutions, substituting these points into the objective function to find the optimal value, and identifying the optimal solution. It then provides examples demonstrating this process and different types of solutions that can arise such as unbounded, infeasible, and optimal.

1. GRAPHICAL METHOD

5. 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 x 2 x 1 Example Max z = 5 x 1 + 7 x 2 s.t. x 1 < 6 2 x 1 + 3 x 2 < 19 x 1 + x 2 < 8 x 1 , x 2 > 0 Every point is in this nonnegative quadrant

6. 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 x 2 x 1 x 1 < 6 (6, 0) Example (Cont…) Max z = 5 x 1 + 7 x 2 s.t. x 1 < 6 2 x 1 + 3 x 2 < 19 x 1 + x 2 < 8 x 1 , x 2 > 0

7. 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 2 x 1 + 3 x 2 < 19 x 2 x 1 (0, 6.33) (9.5 , 0) Max z = 5 x 1 + 7 x 2 s.t. x 1 < 6 2 x 1 + 3 x 2 < 19 x 1 + x 2 < 8 x 1 , x 2 > 0 Example (Cont…)

8. 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 x 2 x 1 x 1 + x 2 < 8 (0, 8) (8, 0) Max z = 5 x 1 + 7 x 2 s.t. x 1 < 6 2 x 1 + 3 x 2 < 19 x 1 + x 2 < 8 x 1 , x 2 > 0 Example (Cont…)

9. 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 2 x 1 + 3 x 2 < 19 x 2 x 1 x 1 + x 2 < 8 x 1 < 6 Max z = 5 x 1 + 7 x 2 s.t. x 1 < 6 2 x 1 + 3 x 2 < 19 x 1 + x 2 < 8 x 1 , x 2 > 0 Example (Cont…)

10. 8 7 6 5 4 3 2 1 1 2 3 4 5 6 7 8 9 10 x 2 x 1 Example (Cont…) A (0,0) (6,0)B (6,2)C (5,3)D (0,6.33)E

17. Example (Cont…) P1 P2 (0,0) (4,0) (0,6) (2,6) (4,3) ( 6,0) A B C D E

18. Example (Cont…) Objective Function : Max Z= 3 P1 + 5 P2 Corner Points Value of Z A – (0,0) 0 B – (4,0) 12 C – (4,3) 27 D – (2,6) 36 E – (0,6) 30 Optimal Point : (2,6) Optimal Value : 36

19. Example Min z = 5 x 1 + 2 x 2 s.t. 2 x 1 + 5 x 2 > 10 4 x 1 - x 2 > 12 x 1 + x 2 > 4 x 1 , x 2 > 0

20. 5 4 3 2 1 1 2 3 4 5 6 x 2 4 x 1 - x 2 > 12 2 x 1 + 5 x 2 > 10 x 1 Example Min z = 5 x 1 + 2 x 2 s.t. 2 x 1 + 5 x 2 > 10 4 x 1 - x 2 > 12 x 1 + x 2 > 4 x 1 , x 2 > 0 x 1 + x 2 > 4

21. 5 4 3 2 1 1 2 3 4 5 6 x 2 x 1 Feasible Region This is the case of ‘Unbounded Feasible Region’. Example (Cont…) Min z = 5 x 1 + 2 x 2 s.t. 2 x 1 + 5 x 2 > 10 4 x 1 - x 2 > 12 x 1 + x 2 > 4 x 1 , x 2 > 0 A (35/11 , 8/11) B (5,0)

22. Example (Cont…) Objective Function : Max Z= 5x 1 +2x 2 Corner Points Value of Z A – (35/11, 8/11) 191/11 (17.364) B – (5,0) 25 Optimal Point : (35/11,8/11) Optimal Value : 191/11=17.364

23. Example Max z = 3 x 1 + 4 x 2 s.t. x 1 + x 2 > 5 3 x 1 + x 2 > 8 x 1 , x 2 > 0

24. Example x 1 3 x 1 + x 2 > 8 x 1 + x 2 > 5 5 5 8 2.67 Max z = 3 x 1 + 4 x 2 s.t. x 1 + x 2 > 5 3 x 1 + x 2 > 8 x 1 , x 2 > 0 Feasible Region This feasible region is unbounded, hence z can be increased infinitely. So this problem is having a Unbounded Solution .

25. Example Max z = 2 x 1 + 6 x 2 s.t. 4 x 1 + 3 x 2 < 12 2 x 1 + x 2 > 8 x 1 , x 2 > 0

26. Example Max z = 2 x 1 + 6 x 2 s.t. 4 x 1 + 3 x 2 < 12 2 x 1 + x 2 > 8 x 1 , x 2 > 0 x 2 x 1 4 x 1 + 3 x 2 < 12 2 x 1 + x 2 > 8 3 4 4 8 In this example, common feasible region does not exist and hence the problem is not having a optimal solution. This is the case of infeasible solution.