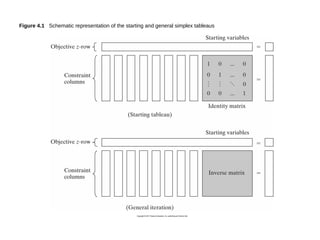
This document discusses duality in linear programming. It defines the dual problem as another linear program systematically constructed from the original or primal problem, such that the optimal solutions of one provide the optimal solutions of the other. The document provides rules for constructing the dual problem based on whether the primal problem is a maximization or minimization problem. It also gives examples of writing the dual of a primal problem and solving both problems to verify the optimal objective values are equal. Finally, it discusses economic interpretations of duality and the relationship between primal and dual problems and solutions.

1. Ch.4
Duality and Post Optimal Analysis

2. Introduction
• One of the most important discoveries in the early
development of linear programming was the
concept of duality and its ramifications.
• discovery revealed that every linear programming
problem has associated with it another linear
programming problem called the dual. The
relationships between the dual problem and
the original problem (called the primal) prove
to be extremely useful in a variety of ways.
• We shall describe many valuable applications of
duality theory

3. Definition of the Dual
problem
• The dual problem is an LP defined systematically
from the primal (original) LP model.
• The two problems are so closely related
– the primal optimum solution automatically
provides the optimal solution to the dual.
• The primal problem represents
– a resource allocation case
• the dual problem represents
– a resource valuation problem.
• Duality help simplification of the simplex problem.

4. Rules for constructing the dual
problem
First modify the give PLP in the standard equation form
and use the following table.
Primal
Problem
Dual Problem
Objective Objective Constraints
Type
Variable sign
Maximization Minimization ≥ unrestricted
Minimization Maximization ≤ unrestricted

5. Figure 4.1 Schematic representation of the starting and general simplex tableaus

6. Example (1)
• Write the dual for the following primal problem:
• Maximize Z= 5x1 + 12x2 + 4x3
Subject to: x1+2x2+x3 ≤ 10
2x1- x2 + 3x3 = 8
x1,x2,x3 ≥ 0
What if you considered artificial variables to
change to standard form rather than equation
form???.....Try

7. Example (2)
• Write the dual for the following
primal problem
Maximize Z= 5x1 + 12x2 + 4x3
Subject to: x1+2x2+x3 ≤ 10
2x1- x2 + 3x3 = 8
x1,x2,x3 ≥ 0

8. Maximize Z= 5x1 + 12x2 + 4x3
Subject to: x1+2x2+x3 ≤ 10
2x1- x2 + 3x3 = 8
x1,x2,x3 ≥ 0
Minimize w = 10y1 + 8y2
Subject to: y1 + 2y2 ≥5
2y1 - y2 ≥ 12
y1 + 3y2 ≥ 4
y1 ≥ 0
y2 unrestricted

9. Optimal Dual Solution
• The two methods for finding the
optimal value of the dual problems
• However, dual of the dual is itself the
primal, which means that the dual
solution can also be used to yield the
optimal primal solution automatically.

10. Optimal dual solution.....

11. Maximize Z= 5x1 + 12x2 + 4x3
Subject to: x1+2x2+x3 ≤ 10
2x1- x2 + 3x3 = 8
x1,x2,x3 ≥ 0

12. Verification methods

13. Maximize Z= 5x1 + 12x2 + 4x3
Subject to: x1+2x2+x3 ≤ 10
2x1- x2 + 3x3 = 8
x1,x2,x3 ≥ 0
Minimize w = 10y1 + 8y2
Subject to: y1 + 2y2 ≥5
2y1 - y2 ≥ 12
y1 + 3y2 ≥ 4
y1 ≥ 0
y2 unrestricted

14. Example...continued..
solution..

15. Primal-dual relationship

16. Primal-dual objective values

17. Economic Interpretations
●
●
●
●
●