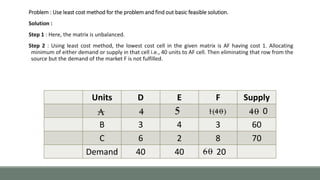
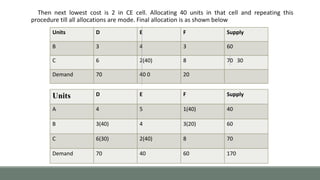
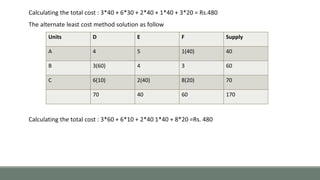
The document outlines the presentation topic of Modified Distribution Method (MODI Method) for solving transportation problems. It first discusses the prerequisite methods of Least Cost Method, Vogel's Approximation Method and North-West Corner Method. It then explains the steps of MODI Method which involves setting up cost matrices for unallocated cells and introducing dual variables to find the implicit cost and evaluate unoccupied cells to determine if the initial solution can be improved. The document provides an example problem and solution to demonstrate the application of MODI Method.

1. Shri S'ad Vidya Mandal Institute Of Technology
BRANCH : MECHANICAL ENGINEERING
SEMESTER : 7TH SEM
YEAR : 2016-2017
SUBJECT : OPERATIONS RESEARCH (2171901)
PRESENTATION TOPIC : MODIFIED DISTRIBUTION METHOD (MODI METHOD)
ENROLLMENT NO : 130454119006
GUIDED BY : ASST. PROF. JAY SHAH

2. Outline of Presentation:-
1. Prerequisite :
 Least cost Method
 Vogel’s Approximation Method
 North-West Corner Method
2. Modified Distribution Method (MODI) or u-v Method
3. References

3. Least cost method
Step 1: Balance the problem. If not add a dummy column or dummy row as the case may be and
balance the problem.
Step 2: Identify the lowest cost cell in the given matrix. Allocate minimum of either demand or
supply in that cell. If there is a same value of cost allocate to any cell as per your choice
according to demand and supply. Then eliminate that row or column in further procedure.
Step 3: Next search for lowest cost cell. Repeat this procedure till all allocation is not completed.
Step 4: Once all the allocations are over, i.e., availability and demand are satisfied, write
allocations and calculate the cost of transportation.

4. Problem : Use least cost method for the problem and find out basic feasible solution.
Solution :
Step 1 : Here, the matrix is unbalanced.
Step 2 : Using least cost method, the lowest cost cell in the given matrix is AF having cost 1. Allocating
minimum of either demand or supply in that cell i.e., 40 units to AF cell. Then eliminating that row from the
source but the demand of the market F is not fulfilled.
Units D E F Supply
0
B 3 4 3 60
C 6 2 8 70
Demand 40 40 2006
A 4 5 )04(1 04

5. Then next lowest cost is 2 in CE cell. Allocating 40 units in that cell and repeating this
procedure till all allocations are mode. Final allocation is as shown below
Units D E F Supply
A 4 5 1(40) 40
B 3(40) 4 3(20) 60
C 6(30) 2(40) 8 70
Demand 70 40 60 170
Units D E F Supply
B 3 4 3 60
C 6 2(40) 8 70 30
Demand 70 40 0 20

6. Calculating the total cost : 3*40 + 6*30 + 2*40 + 1*40 + 3*20 = Rs.480
The alternate least cost method solution as follow
Calculating the total cost : 3*60 + 6*10 + 2*40 1*40 + 8*20 =Rs. 480
Units D E F Supply
A 4 5 1(40) 40
B 3(60) 4 3 60
C 6(10) 2(40) 8(20) 70
70 40 60 170

7. Vogel’s Approximation Method (VAM)
VAM gives better initial solution than obtained by other methods. Here, the concept of
opportunity cost is considered.
 Opportunity cost is the penalty occurring for not selecting right cell for the allocation. This
opportunity cost is found out by calculating the difference in each row or in each column for cost
coefficients As the value of difference is larger, higher will be the penalty for allocating in second
smallest cell instead of smallest cost cell. So, this shows the penalty for failing to make right
allocating to the smallest cell.

8. Steps involved in the (VAM) method :
1. Balance the problem. If not add a dummy column or dummy row to balance the problem.
2. Opportunity cost is found out by calculating the difference between the smallest and second
smallest element in each row and in each column. Enter the difference in respective column or in
respective row in brackets.
3. Select the row or column from the matrix which has maximum value. In that selected row or
column, select the cell which has minimum cost coefficient. Allocate smallest value of demand or
supply in the cell.
4. Eliminate that allocated row or column and prepare the new matrix.
5. Repeat this procedure until all allocation are not complete.
6. Once all the allocation are over, i.e. availability and demand are satisfied, write allocations and
calculate the cost of transportation.
 Important Points to Remember:
1. If the coefficients in a row or column are same, than difference for that row or column is '0'.
2. In case of tie among the highest penalties, select the row or column having minimum cost. In case
of tie in minimum cost also, select the cell in which maximum allocation can be done. Again, if
there is a tie in maximum allocation value, select the cell arbitrarily for allocation.

9. Since, the matrix is balanced; we should start from step 2.
Here, finding out the difference between the smallest and second smallest for each row and
each column & entering in respective column and row. It is shown in brackets.
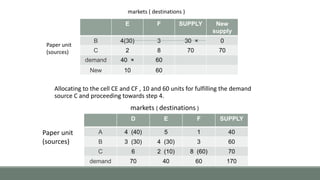
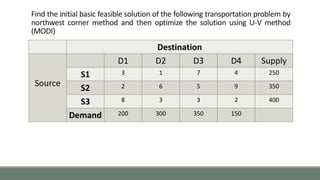
Example :- The paper manufacturing company has three warehouses located in
three different areas, says A, B & C. The company has to send from these
warehouses to three destinations, says D, E & F. The availability from warehouses A,
B & C is 40, 60, & 70 units. The demand at D, E and F is 70, 40 and 60 respectively.
The transportation cost is shown in matrix (in Rs.).
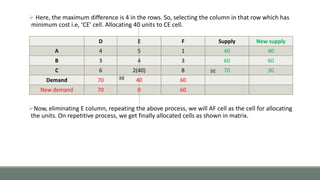
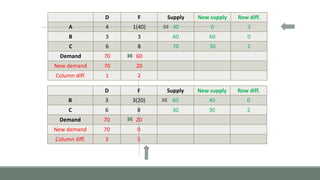
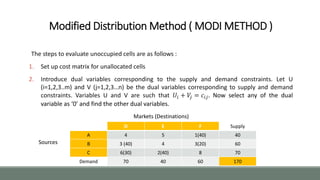
D E F Supply Row Difference
A 4 5 1 40 [3]
B 3 4 3 60 [0]
C 6 2 8 70 [4]
Demand 70 40 60 170
Column Difference [1] [2] [2]

10.  Here, the maximum difference is 4 in the rows. So, selecting the column in that row which has
minimum cost i.e, ‘CE’ cell. Allocating 40 units to CE cell.
D E F Supply New supply
A 4 5 1 40 40
B 3 4 3 60 60
C 6 2(40) 8 70 30
Demand 70 40 60
New demand 70 0 60
Now, eliminating E column, repeating the above process, we will AF cell as the cell for allocating
the units. On repetitive process, we get finally allocated cells as shown in matrix.

11. D F Supply New supply Row diff.
A 4 1(40) 40 0 3
B 3 3 60 60 0
C 6 8 70 30 2
Demand 70 60
New demand 70 20
Column diff. 1 2
D F Supply New supply Row diff.
B 3 3(20) 60 40 0
C 6 8 30 30 2
Demand 70 20
New demand 70 0
Column diff. 3 5

12. Now allocating 40 units to BD cell and 30 units to CD cell, final matrix can be generated as
below:
D E F Supply
A 4 5 1(40) 40
B 3(40) 4 3(20) 60
C 6(30) 2(40) 8 70
Demand 70 40 60 170
Calculating the total cost: 3 40+ 6 30+ 2 40+ 1 40+3 20= Rs 480
VAM method provides most efficient allocation then any other method for obtaining the basic feasible solution.
Checking the above problem for degeneracy, the number of allocated cell must be equal to
R+C-1, i.e 3+3-1=5. Here the solution is non degenerated basic feasible solution.

13. North-West Corner method
•Following steps are involved in above method:
•Step 1: balance the problem . if not add a dummy column or dummy row as the case may be and
balance the problem.
•Step 2: start allocation from the left hand side top most corner cell and make allocations
depending on the availability and demand .if the availability is less than the requirement ,then
for that cell make allocation in unit which is equal to the availability .commonly speaking , verify
which is the smallest among the availability and requirement and allocate the smallest one to
the cell.
•Step 3: when availability or demand is fulfill for that row or column respectively , remove that
row or column from the matrix. Prepare new matrix.

14. •Step 4: then proceed allocating either sidewise or downward to satisfy the rim requirement
continue this until all the allocation are over.
•Step 5 : once all the allocations are over, i.e., availability and demand are satisfied, write
allocations and calculate the cost of transportation.

15. Solution:
Step 1: here the given matrix is balanced. I.e. the demand and supply is same. So the proceeding
towards step 2
step 2: starting the allocation from the left hand side top most corner cell AD. Here the demand
for the market is 70 units and supply available from the source A is 40 . So allocating the
minimum value of this two , we allocate 40 units to cell AD as follow and eliminating source A in
the next step.
D E F SUPPLY New supply
A 4(40) 5 1 40 × 0
B 3 4 3 60 60
C 6 2 8 70 70
demand 70 × 40 60
New 30 40 60
markets ( destinations )
Paper unit
(sources)

16. In the next matrix, since the demand for a market D has not been fulfilled , so
allocating 30 units to the BD cell, which is smallest among supply and demand
for the source B and demand from market D.
now ,since the demand for the market D has been fulfilled , and preparing the
next matrix removing market D . New N-w cell is BE ,which has demand of 4o
units , which can be satisfied by matrix B.
D E F SUPPLY New
supply
B 3(30) 4 3 60 × 30
C 6 2 8 70 70
demand 30 × 40 60
New 0 40 60
Paper unit
(sources)
markets ( destinations )

17. Allocating to the cell CE and CF , 10 and 60 units for fulfilling the demand
source C and proceeding towards step 4.
D E F SUPPLY
A 4 (40) 5 1 40
B 3 (30) 4 (30) 3 60
C 6 2 (10) 8 (60) 70
demand 70 40 60 170
markets ( destinations )
Paper unit
(sources)
E F SUPPLY New
supply
B 4(30) 3 30 × 0
C 2 8 70 70
demand 40 × 60
New 10 60
Paper unit
(sources)
markets ( destinations )

18. Calculating the total cost :
4 × 40 + 3 × 30 + 4 × 30 + 2 × 10 + 8 × 60 = Rs . 870 /-

19. Modified Distribution Method ( MODI METHOD )
When a basic initial feasible solution is obtained, then we have to check for it’s optimality. An
optimal solution is one where there is no other set of roots that will further reduce the total
cost.
Further we have to evaluate each unoccupied cell in table to reduce total cost.
Evaluating the steps will result in the most optimal cost of transportation.

20. Modified Distribution Method ( MODI METHOD )
The steps to evaluate unoccupied cells are as follows :
1. Set up cost matrix for unallocated cells
2. Introduce dual variables corresponding to the supply and demand constraints. Let U
(i=1,2,3..m) and V (j=1,2,3…n) be the dual variables corresponding to supply and demand
constraints. Variables U and V are such that 𝑈𝑖 + 𝑉𝑗 = 𝑐𝑖𝑗. Now select any of the dual
variable as ‘0’ and find the other dual variables.
D E F Supply
A 4 5 1(40) 40
B 3 (40) 4 3(20) 60
C 6(30) 2(40) 8 70
Demand 70 40 60 170
Markets (Destinations)
Sources

21. Modified Distribution Method ( MODI METHOD )
Now the newly formed matrix will be:
Solving the filled cell allocation,
U1+V3= 1 U3+V1= 6 U2+V3= 3
U2+V1= 3 U3+V2= 2
Taking U3 (any) variable as ‘0’.
We get, V1=6; V2=2; V3=6, U1=-5; U2=-3
𝑈𝑖 𝑉𝑗 𝑉1 𝑉2 𝑉3
𝑈1 1
𝑈2 3 3
𝑈3 6 2

22. Modified Distribution Method ( MODI METHOD )
Rewriting the matrix with U and V values,
3. Find out implicit cost. Implicit cost is summation of dual variables of row and column for each
unoccupied cell. Then, vacant cell evaluation is carried out by taking the difference for each
unoccupied cell.
Evaluation of cell = 𝑐𝑖𝑗 − (𝑈𝑖+𝑉𝑗)
𝑈𝑖 𝑉𝑗 6 2 6
-5 1
-3 3 3
0 6 2

23. Examine the sign of each dij
1. If dij > 0 For i and j then solution is optimal.
2. If dij = 0 For all i and j then solution will remains unaffected but an alternative solution exists.
3. If one or more dij < 0 then the initial solution can be improved by entering unoccupied cells in basis
with the largest negative value of dij
 Construct a closed loop For the unoccupied cell with largest negative value of dij . Start the closed loop
with the selection of unoccupied cells & mark (+) sign in the cell and trace a path along the rows (columns)
to unoccupied cell and mark (-) sign and continue to column (row) to an occupied cell with (+) sign and (-)
sign alternatively & back to the selected unoccupied cell.
Select the smallest value among the cells with (-) sign and allocate this value to the selected unoccupied
cell and add it to other occupied cells marked with (+) sign and subtract it from the occupied cells marked
with (-) sign.
 Obtain the initial solution and calculate a new total cost.
 The procedure terminate when all dij ≥ 0 For all unoccupied cells.

24. Find the initial basic feasible solution of the following transportation problem by
northwest corner method and then optimize the solution using U-V method
(MODI)
Destination
Source
D1 D2 D3 D4 Supply
S1 3 1 7 4 250
S2 2 6 5 9 350
S3 8 3 3 2 400
Demand 200 300 350 150

25. Solution:-
Phase 1 : Finding initial basic feasible solution using north-west cornor
method.
D1 D2 D3 D4 Capacity
S1 3 1 7 4
S2 2 6 5 9
S3 8 3 3 2
Demand
200 50
100250
250 150
Basic feasible solution : 3*200 + 1*50 + 6*250 + 5*100 + 3*250 + 2*150 = Rs.3700

26. Phase 2 : Application of u-v method to optimize the solution.
v1 = v2 = v3 = v4 =
u1 = 3 1 7 4
u2 = 2 6 5 9
u3 = 8 3 3 2
200 50
100250
250 150
Equation for finding out the values of u & v is, ui + vi = cij (allocated cells)
Then find the Penalties by eq :- pij = ui + vi – cij (unallocated cells)
C13 = 0+0-7 = -7
C14 = 0-1-4 = -5
C21 = 5+3-2 = 6
C24 = 5-1-9 = -5
C31 = 3+3-8 = -2
C32 = 3+1-3 = 1
If all the values are ≤ 0 𝑂𝑝𝑡𝑖𝑚𝑎𝑙 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛 𝑖𝑠 𝑜𝑏𝑡𝑎𝑖𝑛𝑒𝑑
But here 6 is the maximum positive value at C21, so new basic cell is C21.

27. 3 1 7 4
2 6 5 9
8 3 3 2
200 50
250
250
100
150
 Take the smallest (-ve) value and add it to both (+ve) values & subtract it from both (-
ve) values
Now, find out the new values of u & v, by eq ui + vi = cij (allocated cells) for next table
v1 = v2 = v3 = v4 =
u1 = 3 1 7 4
u2 = 2 6 5 9
u3 = 8 3 3 2
200
250
50
250
100
150

28. Then find the Penalties by eq :- pij = ui + vi – cij (unallocated cells)
C11 = 0-3-3 = -6
C13 = 0+0-7 = -7
C14 = 0-1-4 = -5
C24 = 5-1-9 = -5
C31 = 3-3-8 = -8
C32 = 3+1-3 = 1
3 1 7 4
2 6 5 9
8 3 3 2
If all the values are ≤ 0 𝑂𝑝𝑡𝑖𝑚𝑎𝑙 𝑠𝑜𝑙𝑢𝑡𝑖𝑜𝑛 𝑖𝑠 𝑜𝑏𝑡𝑎𝑖𝑛𝑒𝑑
But here 1 is the maximum positive value at C32, so new basic cell is C32.
200
250
50 100
250 150

29.  Take the smallest (-ve) value and add it to both (+ve) values & subtract it from both (-
ve) values
Now, find out the new values of u & v, by eq ui + vi = cij (allocated cells) for next table
v1 = v2 = v3 = v4 =
u1 = 3 1 7 4
u2 = 2 6 5 9
u3 = 8 3 3 2
200
250
50 200
150
150
Then find the Penalties by eq :- pij = ui + vi – cij (unallocated cells)
C11 = 0-2-3 = -5
C13 = 0+1-7 = -6
C14 = 0-0-4 = -4
C22 = 4+1-6 = -1
C24 = 4+0-9 = -5
C31 = 2-2-8 = -8
Calculating the total transportation cost : 1*250 + 2*200 + 5*150 + 3*50 + 3*200 + 2*150 =
Rs.2450

30. Reference:-
 Content from Operation Research by Dr.Akshay A. Pujara & Dr. Ravi Kant.
 Tables (Self Prepared by group members)